Shape of the moon

Geometry Level 4

The moon can be modeled as a sphere of radius $R$ , at a large distance $d\, (\gg R)$ from us. The moon is illuminated by a parallel beam of sunlight, which is the part of its surface that we see. Depending on the angle between our line of sight and the incoming sunlight, the moon may appear as the typical "moon shape" as shown above.

Which of these two methods correctly describes how we see the moon from the earth?

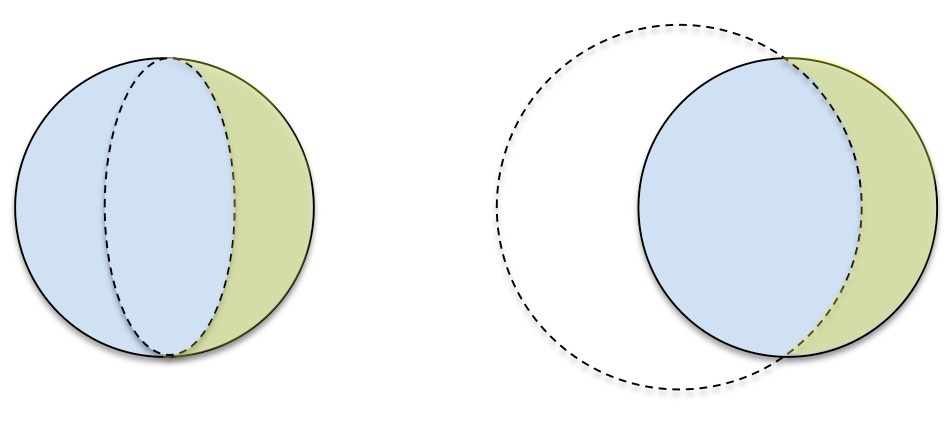
Pick two diametrically opposed points $A$ and $B$ , and then draw an ellipse with major axis $AB$ and take one of the two parts of the circle cut out as in the diagram below left.
Pick two diametrically opposed points $A$ and $B$ , then draw a second, larger circle which intersects the original circle at points $A$ and $B$ , and then take one of the two parts of the circle cut out as in the diagram below right.

Method 1 Method 2 Neither method Both methods; they result in the same kind of shape

1 solution

Arjen Vreugdenhil
May 24, 2017

Method 1 is correct. The boundary between light and dark on the moon sphere is a circle $\mathcal C$ centered at the sphere's center. The projection of a circle onto a plane is an ellipse, whose midpoint is the projection of the center of the circle. (Here we assumed that no perspectival distortion takes place due to differences in distance to the observer; this is warranted by $d >> R$ .)

To see that method 2 is different, look at the angles of intersection. In method 1, the circle and ellipse both have a horizontal tangent in the intersection points $A$ and $B$ ; thus they intersect at $0^\circ$ . In method 2, the two circles intersect at a non-zero angle.

How do we know that there exists 2 diametrically opposite points on the moon-sphere which are illuminated?

Calvin Lin Staff - 4 years ago

The illuminated part of the moon is a half-sphere, bounded by a great circle. For every point on a great circle, its antipode is also part of that great circle.

Arjen Vreugdenhil - 4 years ago

Right, that's my question. How do we know that "the illuminated part of the moon is a half-sphere"? Is that an assumption of the setup, or can that be proven?

Calvin Lin Staff - 4 years ago

@Calvin Lin – An easy way to see this: model the moon as a sphere of radius $R$ centered at $(0,0,0)$ . Assume w.l.o.g. that the sunlight comes from the positive $z$ -direction. Then all points with $z > 0$ will be illuminated, and the boundary is the intersection of the sphere with the plane $z = 0$ , i.e. the great circle $(x,y,z) = (R\cos \phi,R\sin\phi,0)$ .

For further analysis, consider that a surface element will be illuminated if $\vec n\cdot \vec \ell < 0$ , where $\vec n$ is the normal to the surface and $\vec \ell$ is the direction of the light.

Arjen Vreugdenhil - 4 years ago

Shape of the moon

1 solution

0 pending reports