Shells Losing Energy !
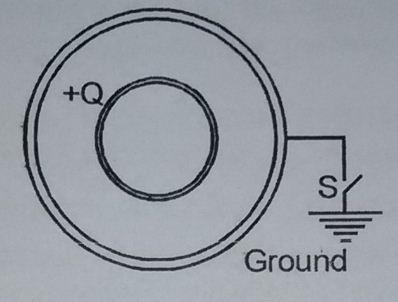 An arrangement of two concentric conducting spherical shells charged initially such that the inner shell (radius =
a
) carries a net charge of
+
Q
while outer shell (radius
b
) carries net charge
0
. If the switch "
S
" is closed, how much electrostatic potential energy would the system lose?
An arrangement of two concentric conducting spherical shells charged initially such that the inner shell (radius =
a
) carries a net charge of
+
Q
while outer shell (radius
b
) carries net charge
0
. If the switch "
S
" is closed, how much electrostatic potential energy would the system lose?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions

Sir ,here,loss in Potential Energy is exactly same as self-energy of conducting sphere . Is there any relation between both of them??
Before the switch is closed there is an induced charge of − Q on the inner surface of the outer shell (radius b ) and an induced charge of + Q on it’s outer surface. Thus the total Potential Energy of the system is U i = 8 π ϵ 0 a b Q 2 ( b − a ) + 8 π ϵ 0 b Q 2
whereas when the switch is closed the outer surface charge + Q is absorbed by the ground and only the charge − Q on the inner surface remains (no change for the inner sphere ), hence the potential energy of the system becomes U f = 8 π ϵ 0 a b Q 2 ( b − a ) . Hence loss in potential energy is 8 π ϵ 0 b Q 2
In the expression Ui shouldn"t be 8 instead of 4
I can't understand the concept of positive charge being absorbed by the ground
Log in to reply
Refer to the concept of Earthing of Conductors -
Because when a body is earthed its potential become same as that of the earth. And since conventionally the earth is considered to be of zero potential hence the body is said to be of zero potential.
Log in to reply
but how can positive charge go to earth
Log in to reply
@Atul Solanki – Electrons flow from the shell to earth. It's the same as positive charges flowing from earth to the shell, just like the conventional electric current
Here,loss in Potential Energy is exactly same as self-energy of conducting sphere . Is there any relation between both of them??
Nice solution
Can't understand why the potential energy before closing the switch is the Ui. Why it is not just the auto energy of the spherical shell of radius a?
A E = 8 π ϵ 0 a Q 2
(I'm sorry my TeX isn't working properly above)
Log in to reply
Correct me if i am wrong,
What you have termed as AUTO ENERGY is what SELF POTENTIAL ENERGY of a body is.
Due to induction, the inner surface of the outer shell accumulates a charge of − Q and the outer surface of the outer shell a charge of + Q .
If you look closely, the outer surface of inner shell and inner surface of the outer shell makes a circular capacitor charged with charge Q . So one has to include the energy stored in the capacitor while writing U i .
And self potential energy for the the outer surface of the outer shell is U s e l f = 8 π ϵ 0 b Q 2
Log in to reply
Yes, I am really sorry, what I call "auto energy" is the self energy (Self is translated as Auto in portuguese and I forgot translating) Thanks.
Got it! You are right, they form a capacitor. I supposed that the radius b shell was sufficiently thin, and I neglected its energy. Thanks
On earthing the outer sphere a negative charge of -Q will appear on it. Hence its energy loss has to be k Q 2 / 2 b , where k is 1 / 4 π ϵ