Shifty Stretch
 If we shift a graph to the right by 4, and then stretch it horizontally by 2 (with respect to the y-axis), this is the same as which of the following transformations?
If we shift a graph to the right by 4, and then stretch it horizontally by 2 (with respect to the y-axis), this is the same as which of the following transformations?
Confused? Read the Stretching Graphs Wiki .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
the graph should be f(x)->f(x-4)-->f(x/2-4/2)ie, f(x/2-2) not f(x/2-4) Also i guess the graph is not for scale
Log in to reply
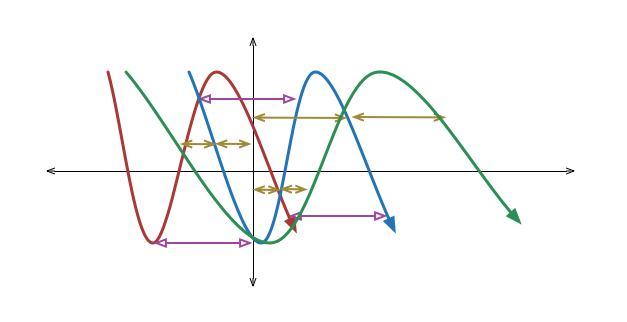
The graphs are actually drawn to scale. The purple arrows are all the same length, IE shift to the right by 4. The yellow arrows represent stretching by 2, because the adjacent arrows have the same length.
Not quite. Consider the point ( x , y ) . It moves to ( x + 4 , y ) and then moves to 2 ( x + 4 ) , y ) . If we have f ∗ ( 2 ( x + 4 ) ) = y = f ( x ) , then if 2 ( x + 4 ) = k , we get x = 2 k − 4 , and so f ∗ ( k ) = f ( 2 k − 4 ) .
Read the Stretching Graphs wiki for more information. This is something that is often not explained well. Many people merely memorized "divide by a 1 " without actually understanding what is happening and why.
Excellent explanation!
What if the graph is x=a (a is a constant)???
Good explanation
We can choose any graph to represent this, so for simplicity start with
f ( x ) = x
Then apply the shift right 4:
f ( x ) = x + 4
Then the horizontal stretch of 2:
f ( x ) = 2 ( x + 4 ) = 2 x + 8
f ( x ) = 2 x + 8 can be described as being stretched horizontally by 2 then shifted right 8.
While stretching the graph, are we assuming the invariant line to be the y-axis? If we take a different line to be the invariant line, then the answer will be different.
Log in to reply
Yes, if we're stretching it horizontally, then we (typically) take the y-axis to be the invariant. Let me add that into the question for clarity.
Log in to reply
@Calvin Lin when the graph is stretched by a factor of 2 , the variable should be divided by 2 instead of multiplying by it so shouldn't the answer be different?
Log in to reply
@Sudeep Salgia – You have to be very carful with what you mean by "the variable is divided by 2", because the variable occurs in many places (but we only divide by 2 in a certain place).
Read Stretching Graphs Wiki for much more detailed information for how to approach an understand this.
@Sudeep Salgia – As mentioned,
You have to be very careful with what you mean by "the variable is divided by 2", because the variable occurs in many places (but we only divide by 2 in a certain place).
Specifically, when you stretch the graph of f ( x ) = x by 2, what you get is f ( 2 x ) = x , which is equivalent to f ( x ) = 2 x . So yes, the "term inside the function" is divided by 2, which is equivalent to "multiplying the x terms by 2".
With graph transformations, you have to be extremely careful with how to approach it, and what your changes are.
Typically, for this method of checking, it is better to use a graph with a lot less symmetry, and a lot more "character". For example, you do not know if the graph was obtained by "stretching in the y-direction by 2 and then translating up by 8".
The transformation is a translation followed by a horizontal expansion. The problem can be reduced by projection onto the x -axis. Then we have that x ↦ 2 ( x + 4 ) = 2 x + 8 that we can in fact be read as a horizontal expansion of factor 2 followed by a right shift by 8 . More formally, if O is the origin, e the unit vector of x -axis, and η O , λ the homothety of center O and coefficient λ , η O ∘ τ 4 e = η O , 2 ∘ τ 4 e ∘ ( η O , 2 − 1 ∘ η O , 2 ) = ( η O , 2 ∘ τ 4 e ∘ η O , 2 − 1 ) ∘ η O , 2 . In virtue of the stabilizer theorem, the conjugate of τ 4 e by the homothety η O , 2 is the tranlation whose vector is just η O , 2 ( 4 e ) = 8 e .
Starting with the graph y = f ( x ) (red graph), if we shift it to the right by 4, we get the graph of y = f ( x − 4 ) (blue graph).
If we stretch the graph of y = f ( x − 4 ) (blue graph) horizontally by 2, we get the graph y = f ( 2 x − 4 ) (green graph).
Since f ( 2 x − 4 ) = f ( 2 1 ( x − 8 ) ) , this graph can also be obtained by a horizontal stretch of 2 , and then a horizontal shift to the right by 8 .