Shooting At Each Other - Part Two

Probability Level 5

A bunch of birds are playing paintball. For the purpose of this problem, assume there is an infinite amount of birds. They all shoot the bird closest to them at the exact same time. What is the maximum amount of times a single bird can get shot?

Assume they play in 3D space. All pairwise distances are distinct.


The answer is 12.

Nathan Ramesh by Nathan Ramesh , 20, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Nathan Ramesh
May 22, 2014

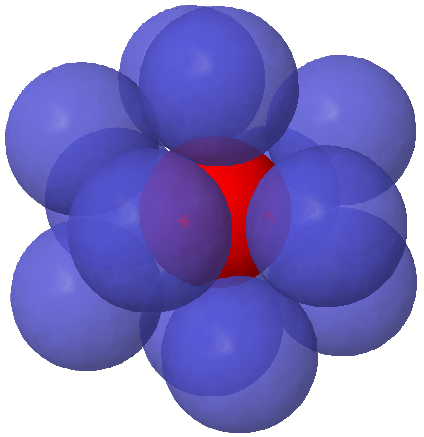
The maximum number of birds occurs when each bird is at a vertex of a regular icosahedron and the bird being shot at is at the center of the icosahedron. It's up to you to prove why.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Sadly, your argument represents a very common misconception. There are actually infinitely many 'distinct' possibilities for 12 loosely packed tangential spheres, which is referred to as the dirty dozen arrangement:

image image (Image from Wikipedia Robertwb )

It takes significant work to show that the answer is not 13. Newton came up with this problem , but was unable to solve it. The 2-dimensional analogue is relatively easy to show. The 4-dimensional analogue of this problem was only solved 10 years ago.

Calvin Lin Staff - 7 years ago

Log in to reply

Why is the problem the same as packing spheres like that?

Nathan Ramesh - 7 years ago

Log in to reply

It is not an equivalent problem. It is a special case of your problem where the shortest distances to a particular bird are the same. Place a bird at the center of each sphere (of equal radius). The blue birds will all attack the red bird, since the spheres do not intersect. As the arrangement is loose, we can slightly perturb these spheres. As such, these are counterexamples to your claim that the only solution is the rigid isocohedron.

So, the question that you also have to deal with is, how do you know that you can't place 13 blue spheres that touch the central red sphere?

Calvin Lin Staff - 7 years ago

Log in to reply

@Calvin Lin – To me, I thought it was obvious that it was impossible to accommodate enough space for a 13th point. I didn't even know it was a famous problem. Apparently, it's not obvious at all.

Nathan Ramesh - 7 years ago

Log in to reply

@Nathan Ramesh – Indeed, hence I started off with "a very common misconception". If you calculate the solid angle of a tetrahedron, you will get a bound of slightly over 13, which offers the possibility of shoving 13 tetrahedrons in there.

TBH, I don't know how to prove that only 12 is possible. I worked on it in the past, and couldn't get far.

Calvin Lin Staff - 7 years ago

Log in to reply

@Calvin Lin – I think the answer is infinity

Movin Jain - 6 years, 12 months ago

@Nathan Ramesh – Hey, we had this exact same discussion together on Google chat, but you didn't believe me. Are you convinced that they are the same problems now that @Calvin Lin has said it too?

Daniel Liu - 6 years, 12 months ago

Thanks for that great reply, Calvin. Entering "12" as the answer was just guesswork, being that the radius of the circumsphere of the icosahedron is just slightly less than its edge length. But I had 3 tries, right?

Michael Mendrin - 6 years, 11 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...