Side by Side
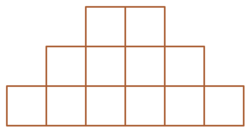 How many ways are there to select 2 unit squares, such that one square is exactly one row above the other?
How many ways are there to select 2 unit squares, such that one square is exactly one row above the other?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
How? There is no specification that the squares, to be chosen, are to be of same size. There are 3 big squares within middle and lowest row that can be chosen for each of the 2 small squares of the topmost row.. => A total of 6 pairs. There is one one big square within the middle and top row, for each of the 6 small squares of the lowest row. => A total of 6 pairs.
and 32 pairs of squares of same size.
=> a total of 32+6+6 = 44
Log in to reply
Ma'm, there is no such option as of 44. I agree with your reasoning, but by "squares" the question meant "Individual Boxes". The question should be edited for removing ambiguity.
Log in to reply
Ya.. a few days ago i could report a problem.. these days i m not being able to see that option. though i double counted.. and gave a wrong answer of 50.. :P
Log in to reply
@Ananya Aaniya – Go to the dot dot dot icon lower left corner of the problem box. There is an option to report problems.
Ah, I edited the question, so that it's just unit squares. Sorry!
Log in to reply
The question is not very cler please rectify. (I could only figure partially what the question meant from reading the comment chain)
Log in to reply
@Nick Baker – What do you feel is not clear about the question? Which phrase do you not understand?
That's only ( 6 × 4 ) + ( 4 × 2 ) = 3 2
this question is not clearly stated
Log in to reply
Can you help me with improving the problem? What do you find is confusing?
I think it is clear if you consider the word 'row'. It seems straight forward that for a square to be exactly one row above another it would have to be a unit square. Although what got me was I had it in my head that it meant the squares also had to be in line vertically!
Log in to reply
I think this problem too clear, we can understand it without any difficulty...
Python: 2.7:
1 2 3 4 5 6 |
|
We observe that for every box in the lowermost row, each of it can be paired with every other box in the second row. Hence, we get number of pairings for every box in lowest row = 6 × 4 = 2 4 . Similarly, for every box in the middle row, each of it can be paired with any box from the topmost row, and we get the number of pairings for every box in the middle row = 4 × 2 = 8 . As there is no row above topmost one, there are 0 possible pairings. Hence, the total number of pairings = 2 4 + 8 = 3 2 .