Similar Right Triangles

Geometry Level 3

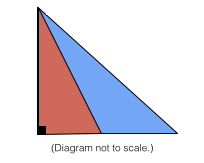In the large right triangle above, an angle bisector is drawn such that the red triangle is similar to the large right triangle. What is the ratio of the red area to the blue area?

1:\sqrt{3}

1:1

1:2

1:3

1:\sqrt{2}

3 solutions

Brian Charlesworth
Nov 12, 2015

As the red triangle is similar to the large right triangle, its apex angle $x$ is the same as the lower right angle of the large right triangle, (and thus also of the blue triangle).

The lower right angle of the red triangle is thus $90^{\circ} - x,$ and so the obtuse angle of the blue triangle is $180^{\circ} - (90^{\circ} - x) = 90^{\circ} + x.$ Since the apex angle of the blue triangle is $x$ we have that

$x + (90^{\circ} + x) + x = 180^{\circ} \Longrightarrow 3x = 90^{\circ} \Longrightarrow x = 30^{\circ}.$

The apex angle of the large right triangle is then $60^{\circ}.$ Now let $a$ be the length of the base of the red triangle, $b$ be the length of the base of the large right triangle and $h$ the common height of both of these triangles. Then we have that

$\tan(30^{\circ}) = \dfrac{a}{h}$ and $\tan(60^{\circ}) = \dfrac{b }{h} \Longrightarrow a = h\tan(30^{\circ}) = \dfrac{h}{\sqrt{3}}$ and $b = h\tan(60^{\circ}) = h*\sqrt{3}.$

The base length of the blue triangle is $b - a = h*\left(\sqrt{3} - \dfrac{1}{\sqrt{3}}\right) = h*\dfrac{2}{\sqrt{3}}.$

Since the red and blue triangles have the same heights, the ratio of their areas will be the same as the ratio of their base lengths, which is

$\dfrac{a}{b - a} = \dfrac{\dfrac{h}{\sqrt{3}}}{\dfrac{2h}{\sqrt{3}}} = \dfrac{1}{2},$ and so the desired ratio is $\boxed{1 : 2}.$

I was confused by your question, which was talking about ratio of AREAS 1 and 2. So my answer was (1:2)^2 = 1:4. Since I couldn't find 1:4 among the choices of answers, I took a chance to answer 1:3 (about which I was almost sure that it would be wrong... I should have tried 1:2...). So I think that you should add a precision specifying that we're looking for the basic ratio of the sides, not the ratio of the areas. Otherwise this is a nice problem with an elegant solution. Thank you for your attention.

Louis-Marie Gaulin - 5 years, 7 months ago

The heights of the red and blue triangles are the same, so the ratio of their areas will be the same as the ratio of their base lengths, which comes out to $1 : 2.$

Brian Charlesworth - 5 years, 7 months ago

I mean AREA = (b.h)/2. Base multiplied by height, divided by 2. Since base is multiplied by the height, the ratio of areas is equal to the square of the basic ratio (or "sides" ratio). It is the same for any plane figure. So here (1/2)^2 = 1/4. For intance, see http://www.mathopenref.com/similartrianglesareas.html Regards.

Louis-Marie Gaulin - 5 years, 7 months ago

@Louis-Marie Gaulin – Yes, I realize that, but since the height $h$ is the same for both the red and blue triangles the ratio of their areas will be identical to that of their base lengths. The red and blue triangles are not similar, so the "squaring" approach you describe does not apply when comparing their areas. The two similar triangles are the red and the large right triangle, (which is composed of both the red and blue triangles). The ratio of their (similar) side lengths is $1:\sqrt{3}$ , so due to their similarity the ratio of their areas will be $(1/\sqrt{3})^{2} = 1/3,$ as your method would indicate. Regards.

Brian Charlesworth - 5 years, 7 months ago

@Brian Charlesworth – Yes. The blue and red areas are not similar. You are absolutely right. Thank you! :)

Louis-Marie Gaulin - 5 years, 7 months ago

@Brian Charlesworth – I would suggest another conclusion for the demo (and simpler, I think). From the second and third paragraphs of the demo, it is proved that the apex angle of the blue triangle measures x=30°. Let's call c and d the two sides of the other apex angle, in the big right triangle. Thus we have sin x = sin 30° = c:d = 1:2. Finally, by the triangle angle bisector's theorem (applied to the big right triangle), we have a:(b-a)=c:d, or a:(b-a)=1:2. Regards.

Louis-Marie Gaulin - 5 years, 7 months ago

@Louis-Marie Gaulin – Great! That is much simpler indeed. Thanks for reminding me of that theorem. :)

Brian Charlesworth - 5 years, 7 months ago

Pamela Barnes
Nov 18, 2015

Once I realized that the red triangle was a 30-60-90 (making the lower right blue angle a 30 deg angle) I used the 1 : $\sqrt{3}$ : 2 property of 30-60-90 triangles, and that the blue triangle was necessarily then isosceles, to determine that the base of the blue triangle must equal the hypotenuse of the red triangle, and was therefore twice the base of the red triangle. (Clearly, the base of the red triangle corresponded to the "1" in the side lengths.)

How did I decide that we were working with 30-60-90 triangles? Because half the top angle of the large triangle had to equal the bottom right blue angle, and the bottom right red angle, then, had to be double the top red angle. That only works with a 30-60-90.

Great observations!

Eli Ross Staff - 5 years, 6 months ago

Vasant Barve
Nov 19, 2015

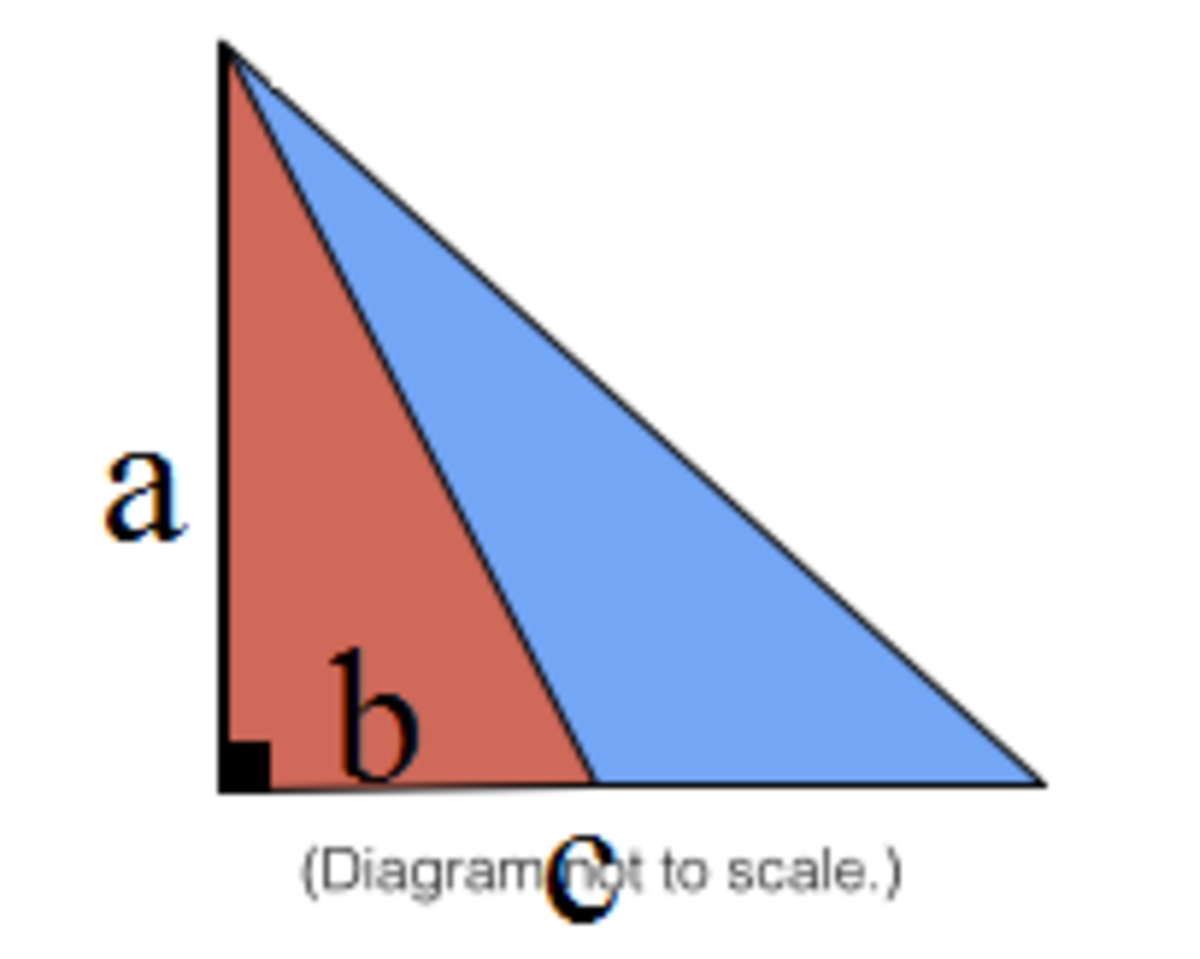Solution For red triangle let height be 'a' and base be b and for larger triangle bace be c. Triangles are similar b/a = a/c a2 = bc a2 + b2 = (c – b)2 Blue triangle is isosceles. = c2 – 2cb + b2 Putting a2 = bc
c =3b Height of both triangles is same so ratio of area is ratio of bases hence Ratio b / (c-b) 1:2

Similar Right Triangles

3 solutions

0 pending reports