A Growing Tension

Classical Mechanics Level 3

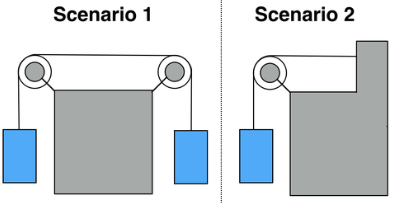
In which scenario is the tension in the rope greater?

Scenario 1 Scenario 2 Tension is same

5 solutions

Josh Silverman Staff
Sep 2, 2015

The important thing to notice in Scenario 1 is that the two masses can only communicate through the rope. It makes no difference to either mass if we replace the pull from the other side with something else that pulls with the same force, like a wall.

As the system is in equilibrium (the masses do not move), the force from the wall would have to be equal to the pull from the mass itself. Thus, we can divide the system in scenario into two pieces as long as we insert a rigid wall, which is exactly the case we find in Scenario 2. This shows that there is no difference between the tension in the rope in either case.

Suppose in scenario 1 on top string is replaced by spring balance, and on either sides connect with two strings????

Srinivas Santoshi - 5 years, 7 months ago

Can you explain? I did not understand what you said...

Kishore S. Shenoy - 5 years, 7 months ago

it will make no difference :D

Syed Baqir - 5 years, 7 months ago

If you were at the plane of symmetry and had to hold both weights up wouldn't you be holding 2kg instead of 1kg?

Alan Greene - 5 years, 6 months ago

In response to above................
Given reason is not satisfactory.......................
If the mass of 1kg removed abruptly from left side in scenario 1, the 1kg mass of right side (of Scenario 1) come down with the rope.....
Vice versa, if same procedure repeat in scenario 2, rope still remain at there same position, and further the wall does not pull the rope toward itself , these means wall is not pulling the rope as in case 1, here the wall is only hold the rope & in case 1, 1kg of r/side contineously applying the force on the rope

azadali jivani - 5 years, 9 months ago

You are wrong,

In Scenario 2 if you pull that rope down the wall will exert opposite Force Tension and will not let the rope to move thats according to Newton's Third Law. the wall will stop applying force as there is no action to cause any reaction

In Scenario 1 as you said if remve one mass, the whole system will move in the direction of the other mass but we are not concerning that case, what we are concerning is the current case as things changes if you change system because in that case the system will not longer be in equilibrium as you ruined everything.

Syed Baqir - 5 years, 9 months ago

ok, thanks

azadali jivani - 5 years, 9 months ago

@Azadali Jivani – For my satisfaction, i am asking here another question, addition to first one....
As an experiment............. In scenario 1, a spring balance is to be inserted in b/w two pulleys, such that both the weights of 1kg each get hang on both sides of the spring balace & vice versa in scenario two one spring balance also inserted in b/w pulley & wal,
?.....I think in the case one, spring balance shows the reading of 2 kg & in case 2
spring balance shows the reading of 1 kg, but as per laws or we say that walls is also pulled, the spring balance should be shown 2 kg in case 2
This experiment shows that the system is remain in equilibrium position but tension on the rope in case 1 is greater than in the case two. this, i am not saying but spring balance itself shows

azadali jivani - 5 years, 9 months ago

@Azadali Jivani – Let me answer your question by asking why you are putting spring balance in between two pulleys, But let say for some reason you put spring balance between masses and pulleys it will show you nothing 0 Kg because tension in that point cancel each other out.

It is same as there is wall in the place of that spring balance Hence, Tension is same in both scenario.

If you put spring balance in scenario 2 it is same as putting spring balance is scenario 1 ignoring the other side hence 1 kg will be shown at the balance .

Syed Baqir - 5 years, 9 months ago

@Syed Baqir – ok, thanks

azadali jivani - 5 years, 9 months ago

It is only when there is a action(force) that there will be a reaction.

Kishore S. Shenoy - 5 years, 8 months ago

Simon Esslemont
Sep 2, 2015

For every action there is an equal but opposite reaction. N3LOM

Observe the weights are in equilibrium.

In S2 the wall "pulls" on the rope with the same effort as the hanging mass "pulls"

S1 is reflective of S2. The second weight is equivalent of the force the wall makes in S2

Marc Brothers
Sep 6, 2015

I may have oversimplified things, but this was how I approached it. The wall is pulling with sufficient force to suspend 1 kilogram. It is certainly capable of anchoring more, but that is not what presents (otherwise the 1 kg weight would move, and not remain in suspension). In scenario 2, the suspended 1kg weight is also pulling with sufficient force to suspend 1 kilogram. The fact that it is not capable of pulling more is irrelevant.

Mega Newton
Sep 4, 2015

Brilliant Question !!!!!!!!!!!!

Hadia Qadir
Sep 3, 2015

The wall is not pulling on the rope, so Newton's 3rd law of motion does not apply in this way in this situation. However, the tenion in the ropes is the same in both scenarios.

The wall is pulling the rope But the magnitude is same as the weight pulling the rope down.

Syed Baqir - 5 years, 9 months ago

A Growing Tension

5 solutions

0 pending reports