Find Father's age

$f - 5 = 3(s - 5) \Rightarrow f = 3s - 10$

$f + 15 = 2(s + 15) \Rightarrow f = 2s + 15$

$3s - 10 = 2s + 15 \Rightarrow s = 25 \Rightarrow f = 65$

$\text{The father is } \boxed {65} \text { years old now.}$

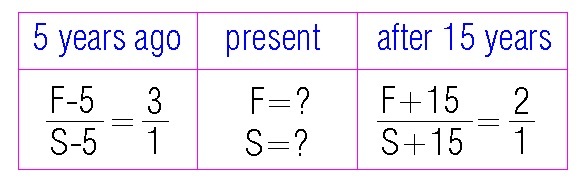Let $F$ be the present age of the father and $S$ be the present age of the son

5 years ago:

$\dfrac{F-5}{S-5}=\dfrac{3}{1}$

Cross-multiplying, we get

$F-5=3(S-5)$

Applying the distributive property, we get

$F-5=3S-15$

We want to isolate $S$ on one side of the equation, so that we can easily compute for the required in the problem which is $F$ ,

Adding $15$ to both sides, we get

$F+10=3S$

Dividing both sides by $3$ , we get

$\boxed{S=\dfrac{F+10}{3}}$

after 15 years:

$\dfrac{F+15}{S+15}=\dfrac{2}{1}$

Cross multiplying, we get

$F+15=2(S+15)$

Applying the distributive property, we get

$F+15=2S+30$

We want to isolate $S$ on one side of the equation for easy substitution,

Subtracting $30$ from both sides, we get

$F-15=2S$

Dividing both sides by $2$ , we get

$\boxed{S=\dfrac{F-15}{2}}$

Equate S=S: Since $S$ in the first equation is equal to the $S$ in the second equation, we equate them

$\dfrac{F+10}{3}=\dfrac{F-15}{2}$

Cross multiplying, we get

$2F+20=3F-45$

Adding both sides by $45$ , we get

$2F+65=3F$

Subtracting $2F$ from both sides, we get

$\boxed{\color{#D61F06}F=65~years~old}$

The difference between the two data points is 20 years.

Father's current age = f

$\large (\frac{f+15}{2}) - (\frac{f-5}{3}) = 20$

Turning both fractions into their own respective equivalent fractions with a common denominator.

$\large (\frac{3f+45}{6}) - (\frac{2f-10}{6}) = 20$

Multiply by 6.

$(3f+45) - (2f-10) = 120$

Simplify.

$f+55 = 120$

Subtract 55.

$\large f = \boxed{65}$

---

For an explanation of the opening expression, we can verify that $(\frac{f+15}{2}) - (\frac{f-5}{3}) = 20$ by virtue of the son also ageing 20 years over the same time $(s+15) - (s-5) = 20$

---

If

$\large \frac{f+15}{s+15} = 2$

then

$\large \frac{f+15}{2} = s+15$

---

And if

$\large \frac{f-5}{s-5} = 3$

then

$\large \frac{f-5}{3} = s-5$

---

So

$\large (\frac{f+15}{2}) - (\frac{f-5}{3}) = (s+15) - (s-5) = 20$

The father's present age is $x$ and son's $y$

$5$ years ago $(x-5) : (y-5) = 3 : 1$

, $\dfrac{x-5}{y-5}$ = $\dfrac{3}{1}$

$⇒ x - 5 = 3y - 15$

$⇒x - 3y = 5 - 15$

$⇒ x - 3y = -10...........................(1)$

Now, $15$ years from now $(x+15) : (y+15) = 2 : 1$

$⇒$ $\dfrac{x + 15}{y +15}$ = $\dfrac{2}{1}$

$⇒ x + 15 = 2y + 15 = 2y +30$

$⇒ x + 2y =30 -15$

$⇒ x- 2y = 15.......................................................(2)$

From equation (1) and (2) ,

 x - 3y = - 10

 x- 2y =    15

(-) (+) (-)

$-y = -25$

$y = 25$

Now, father's age

$\Rightarrow x - 2 × 25 =15$

$⇒ x = 15 + 50$

$x = 65$

Therefore , father's Present age is $\boxed{65}$

The father is 3x times older than his son 5 years ago and after 20 years total the father is 2x times older than his son so we can do this ecuation:

3x + x = 2x + x + 20
3x + x = 3x + 20
X= 20
So the son must be 20 years and the father 60 years 5 years ago. Then now they are 25 years old and 65 years old. And after 15 years they are 40 and 80 so that means the awnser is correct.

suppose, 5 years ago, fathers age was x and sons age was y.

so,the ratio was x/y =3/1

         or, x =3y..............................(1)

again, 15 years from now fathers age will be x=(x+20) and sons age will be y=(y+20)

so,the ratio will be , x+20 /y+ 20 = 2/1

                    or,  x=2y +20.....................(2)

now, 3y = 2y +20..........................(x=x)

       or,  y=20

so, the current age of father is= x+5= 3 x 20 +5=65........................[using equation 1]

Please don't use "X times older than you" as equivalent to "X times as old as you". They don't mean the same thing.