Simple Geometry Problem
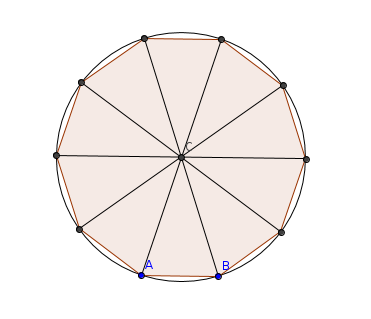
If the decagon is inscribed in a unit circle, what is the length of A B in the diagram below?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Well, yeah, take advantage of my stupidity, why don't you? Haha!, must've skipped my mind. Nice solution! Straightforward and easy to understand.
Yes, sometimes we should think out of the box
This problem is for my friend @Milan Milanic , it's not as interesting, but was something cool I came across while doing geometric constructions. To solve it is really, really simple. It is a 10-gon, so we simply take 1 0 3 6 0 = 3 6 , and because we have a unit circle, we get an isosceles triangle with side lengths 1 and a 36 degree angle. From there, there are of course several ways to solve it, here's the most apparent:
Using law of cosines: a 2 = 1 2 + 1 2 − 2 ( 1 ) ( 2 ) c o s ( 3 6 ) , and we end with a = 0 . 6 1 8 . This is just a simple golden triangle.

Oh, thanks bud @Drex Beckman .
I solved this one using elimination method. I started with something like:
sin 3 6 ° A B = sin 7 2 ° 1 so the answer would be A B = 2 × c o s 3 6 ° 1 (after I put it into calculator, now I see that solution is that number ϕ , I didn't know for that number).
But, since I figured this ought to be done without calculator, finding cos 3 6 ° was a bit troublesome and I was near cancelling (guess I have some conflict with those calculators :D). But.... A B is obviously smaller than one and only one of offered solutions fits in that role.
Therefore, elimination saves the day!
I didn't get notification for at-mention of yours. I saw it accidentally in solution section while searching for the correct way. I guess my first idea is correct to some extent.
Log in to reply
Yeah, I need to think through my multiple choice answers better. Second time I've done something like that... Anyhow your approach with the law of sines seemed spot on, just instead of 2 c o s ( 3 6 ) 1 , You needed s i n ( 7 2 ) s i n ( 3 6 ) . But sounds like you had it anyway. Thought you might find that interesting, golden ratio and all. Thanks!
Log in to reply
But calculator is necessary? Right?
Also, sin 2 x = 2 × sin x × cos x .
Therefore: sin 7 2 ° = 2 × sin 3 6 ° × cos 3 6 °
I don't know why I know these rules. Nice problem (probably didn't tell that until). Maybe this will inspire me. Today, I seriously lack inspiration. Probably because my vacation is ending.
Log in to reply
@Milan Milanic – Yeah, you can use a calculator. It doesn't say anywhere not to use one. ;) I actually did not remember that rule, but then again, I haven't taken trig for over a year. So interesting approach. It's not as clever as you problems, but maybe can give you some inspiration. :)
Observe that AB is smaller than one. Hence the only option that is possible is phi.