CD perpendicular to AB
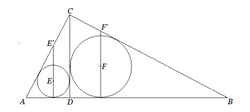Let
A
B
C
be a triangle right angled at
C
. We are given that
C
D
⊥
A
B
and
F
is the center of the inscribed circles of the triangles
A
D
C
and
B
D
C
. Parallel lines through
E
and
F
with
C
D
meet
A
C
and
B
C
at points
E
′
and
F
′
.
Denote n = C F ′ C E ′ and that n is a rational number of the form q p for coprime positive integers p and q . Find the value of p 3 + q 3 .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
It is easy to show that CE' =CF' .
Can you tell me how
Log in to reply
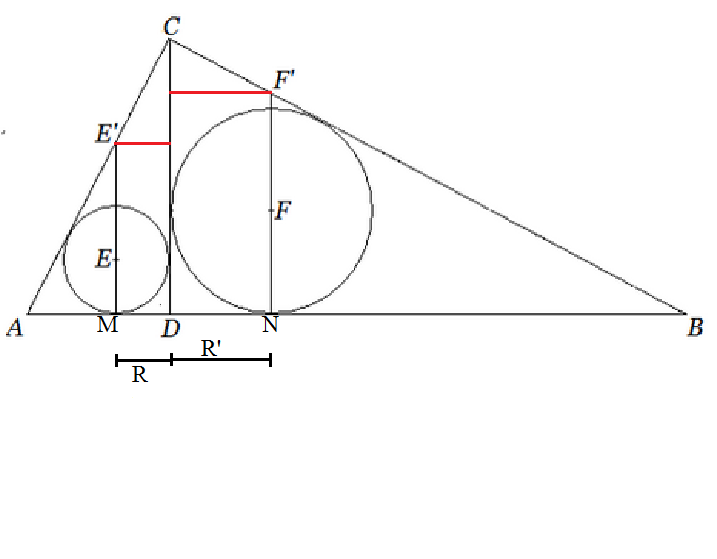Use simple properties of Similar Right angled triangles.
1.) Perpendicular from the vertex opposite to hypotenuse to opposite side (ie. CD) of such triangle divides it into 2 triangles which are similar. Here , △ A D B ≅ △ C D B .
2.) Ratio of the inradii of these two triangles formed is equal to the ratio of any other pair of corresponding sides of the triangle. Here, R ′ R = B C A C = cot ∠ C A B = tan ∠ E ′ C D . ∠ E ′ C D = θ . Here is what we wanted... R csc θ = R ′ sec θ .
Log in to reply
it is not correct ,,, i supposed that the triangle is isosecles to solve it so it's not correct ..and i can show you that
Log in to reply
@Ahmed Moh AbuBakr – You should better show it first
Tell me what the equality of the ratios has to do with the , equality of CE' andCF'. It is not connected directly to it.But your perception is only about it's specific case.Try getting the ratio of CE' and CF' for some arbitrary angles or comment on my solution.
Log in to reply
to make r/r' =ad/db your problem is not correct at all @Gaurav Jain
Log in to reply
It is AC/BC actually , if you are confused. Try this also .
Log in to reply
@Gaurav Jain – no it can't be man exept when 2x=45
@Gaurav Jain – the ratios are not equal so that make AD/DB not equal to R/R'
Log in to reply
@Ahmed Moh AbuBakr – Again !! the same doubt it is AC/BC =R/R'. NOT...... AD/DB. be sure.
Log in to reply
@Gaurav Jain – man ... concentrate ... AC/BC=(AD)^2/(DB)^2 by similarity
Log in to reply
@Ahmed Moh AbuBakr – Ha ha , you want me to concentrate on your mistake !! This is where you are getting confused. rotate triangle ADC clockwise keeping D intact to overlap AD with CD , then see. Don't take it wrongly and let it be a polite conversation. I appreciate you for trying to keep your point as well.
Log in to reply
@Gaurav Jain – AC/CB can't be equal to R/R'
@Gaurav Jain – sorry AC/BC=(AD^2)+(DB^2) it is the same man
As the given conditions do not specify a particular right angled triangles or a particular group of right angled triangles , so the ratio must be the same for any type of tringle , so simply take a isoceles right angled triangled triangle and eidily find CE'=CF'.