Simple Harmonic (1).
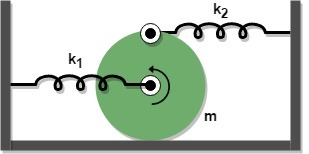
A thin disc of mass m is connected to two ideal, massless springs of spring constants k 1 and k 2 , using two frictionless axles: one attached to the center of the disc and the other at its topmost point. The friction between the disc and the ground below is sufficient for pure rolling motion. The disc is given a small displacement from its equilibrium position and released. The time period of small oscillations of the disc can be expressed as T = 2 π b ( c k 1 + d k 2 ) a m , where ( a , b ) , ( a , c ) , ( a , d ) , ( c , d ) are pairwise coprime positive integers.
Calculate a + b + c + d .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
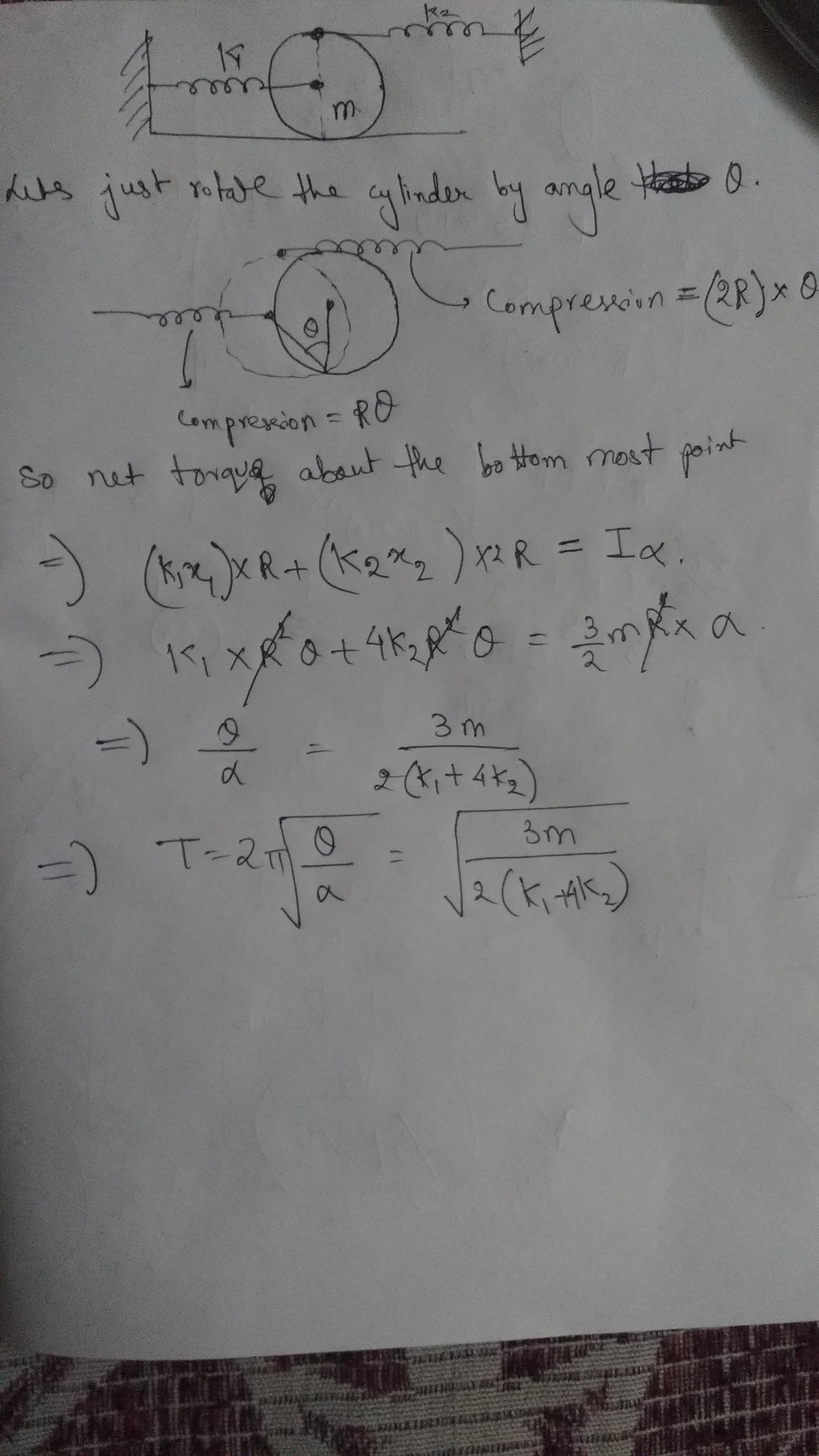
Good solution! Thanks for posting. :)
Log in to reply
What's your method? Torque or energy?
Log in to reply
Energy I like to use.
Log in to reply
@Tapas Mazumdar – @Tapas Mazumdar Ummm, could you please elaborate on the Energy method??? How do we use it??
Hey can you tell me which is the plane in here at this question given https://brilliant.org/problems/flux-and-symmetry/?ref_id=1486557
Log in to reply
I think the plane surface is the part sketched in blue. Bounded as a triangle in positive part and as a semi-infinite rectangle in negative part. Nevertheless, seems intimidating to be honest.
Log in to reply
@Tapas Mazumdar – Hmmm. Let's try in the way you said. As taking only the triangle didn't fetched me up the correct answer
Consider the origin to be placed at the bottom left of the system. The location of the fixed end of the left spring is ( 0 , R ) and that of the right spring is ( L , 2 R ) where L is the separation between the two fixed ends. Let the natural length of the first spring be L 1 and that of the second spring on the right be L 2 . At equilibrium:
L = L 1 + L 2
Consider a general time t where the disc rotates counterclockwise by an angle θ where theta. Let the coordinates of the COM of the disk be ( x , R ) . Therefore, the coordinates of the point of attachment of the second spring with the disk are:
x 2 = x + R sin θ y 2 = R + R cos θ
Also, since the disk purely rolls:
x ˙ = R θ ˙
Integrating:
x = R θ + C
When θ = 0 , then the system is in equilibrium and therefore x = L 1 . Then:
x = R θ + L 1
Now, the kinetic energy of the purely rolling disk is:
T = 2 m x ˙ 2 + 2 1 ( 2 m R 2 ) θ ˙ 2 = 4 3 m R 2 θ ˙ 2
The potential energy of the system is:
V = 2 k 1 ( x − L 1 ) 2 + 2 k 2 ( ( L − x 2 ) 2 + ( 2 R − y 2 ) 2 − L 2 ) 2
Plugging in all expressions and simplifying gives:
V = 2 k 1 R 2 θ 2 + 2 k 2 ( ( L 2 − R θ − R sin θ ) 2 + ( R − R cos θ ) 2 − L 2 ) 2
Now, if we were to consider small oscillations, one must consider the case when θ is small. By applying this approximation:
sin θ ≈ θ cos θ ≈ 1
Plugging these expressions in the expressions for potential energy and simplifying gives:
V = 2 k 1 R 2 θ 2 + 2 4 k 2 R 2 θ 2
Now, the total energy of this system is conserved. This means:
E = T + V
Since energy is conserved:
d t d E = 0 = ( 2 3 m R 2 θ ¨ + ( k 1 + 4 k 2 ) R 2 θ ) θ ˙
Sine θ ˙ = 0 , then:
2 3 m R 2 θ ¨ + ( k 1 + 4 k 2 ) R 2 θ = 0
∴ ω = 3 m 2 ( k 1 + 4 k 2 )
@Talulah Riley Here you go.
@Karan Chatrath Thank you so much for the solution.
@Karan Chatrath The 4th sentence of your solution , in that it should be of instead of fo.
@Karan Chatrath
Is there any other way to solve it, as by a member above, there is one more solution.
I didn't understand it well. Can you help me to understand his problem.
Thanks in advance.
Log in to reply
I think he has used the concept of the instantaneous centre of rotation. He has treated the point of contact as the axis of rotation at the moment at which he applies the torque analogue of Newton's second law. This concept is not very intuitive to me, so I rely on energy-based approaches.