Simulating Dynamics - 5.0
Difficulty: Quite hard.
Here's an ellipse of equation a 2 x 2 + b 2 y 2 = 1 that's cut off at − 3 . 5 < x < 3 . 5 .
The elliptical surface has friction.
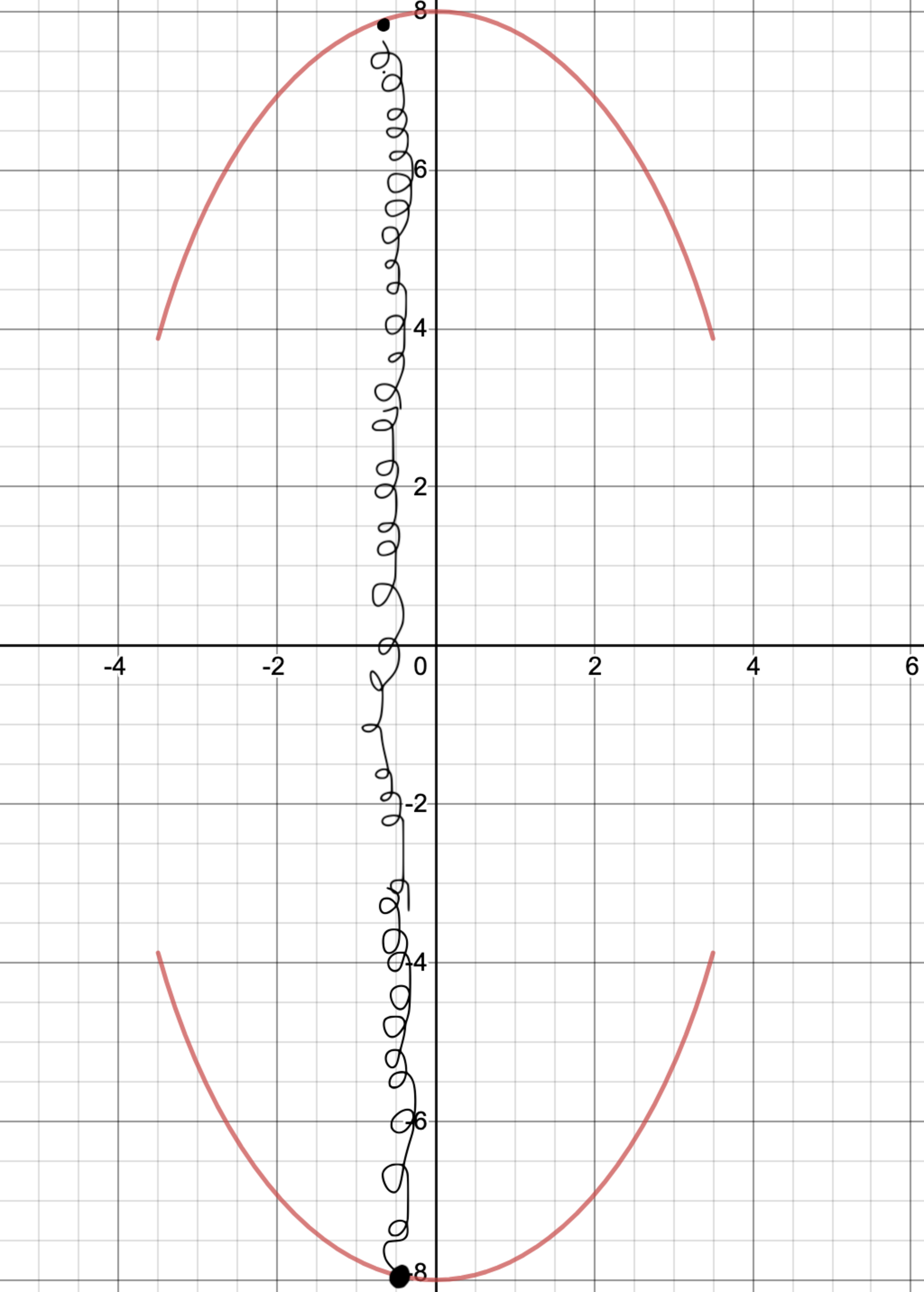
There is a mass at an initial position of x = − 0 . 1 that is sliding on top of the top part of the cut ellipse. There is a spring attached to a control device at the bottom (denoted by the black dot at the bottom part of the ellipse) and the mass at the top.
This control device has the exact same x coordinate as the mass on the top part of the ellipse, and therefore the spring is always parallel to the y axis .
Forget about the bottom mass or anything to do with the bottom part of the ellipse; just know that the control device makes sure the spring is parallel to the y axis. The control device is massless.
The top mass initially has zero velocity and is at a position where it is ensured that it will only slide to the left.
Knowing this, find the time t in seconds it takes for the top mass to fall off, or in other words, to reach x = − 3 . 5 .
Relevant information:
- The mass of the sliding object is m = 3 0 k g
- There is an ambient gravitational acceleration g = 1 0 m / s 2
- The coefficient of friction is μ = 0 . 0 5 , where the friction force is μ N ( N is the normal reaction)
- In the equation of the ellipse, a = 4 and b = 8
- The spring constant is k = 5 N / m
- The natural length of the spring is l = 2 meters
The answer is 5.0856.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
So, do you think my solution's right? I thought that the normal force would just be F g cos ( θ ) + F s cos ( θ )
Btw thanks for solving the problem
Log in to reply
It's difficult to compare, since our approaches are so different. Let's wait for somebody else to solve and see what they got
Log in to reply
True. So, your approach was to derive an equation for the normal force rather than run a routine and resolve forces. What do you think about my graph? Do you think it's a plausible result?
Log in to reply
@Krishna Karthik – Yes, exactly. No force resolution in my approach, which I actually like quite a bit. Whenever we disagree, it is always subtle. So I'm sure your graph is qualitatively fine.
Log in to reply
@Steven Chase – True. That's why I like your solution; it would be less computationally expensive for sure.
Is it just me, or can we no longer see who solved problems? Lol
Log in to reply
That feature has been non-functional for a long time now. I complained about it recently to the staff. Supposedly their developers know about it
@Steven Chase
Nice solution. Upvotes have been awarded.
By the way I am little bit stucking in the second case of this problem, because at that time the velocity of the particle will be different.

Log in to reply
Interesting. I've started to learn about charge and electrostatic force; Coulomb's law.
Log in to reply
@Krishna Karthik Fuck, I thought Steven sir commented me. He usually reply me very less.
Log in to reply
@Talulah Riley – 🤣 So he doesn't reply to you as much?
Log in to reply
@Krishna Karthik – @Krishna Karthik Fuck, Again I thought this time Steven sir replied me.
I posted a new note on it. I'm curious to see if you know how to solve analytically. I was able to determine the form of the result empirically through simulation
Log in to reply
@Steven Chase – Nice numerical approach. I think I found a video on how to solve the ODE analytically.
This one should be doable by hand since the masses are equal. I'll take a look at it tomorrow.
So, from what I gather, you are to write up Coulomb's law for both scenarios, and the final expression must include variables a , b , n , r 0 , t 0
Log in to reply
@Krishna Karthik
FUCK
I thought Steven sir replied me.
Bro if you don't know how to solve it, why are are you replying me.
And one more thing the answer is independent of
r
0
.
@Krishna Karthik
you may feel that I am scolding you.
I am joking with you bro.
Log in to reply
@Talulah Riley – All good. I think I know how to solve it. So far I haven't even attempted it.
I will attempt it now; I am fine with Coulomb's law
Btw the correct grammar is "replying to me"
Log in to reply
@Krishna Karthik – @Krishna Karthik Let's have a one blitz chess match.
Log in to reply
@Talulah Riley – Alright, coming up soon.
Log in to reply
@Krishna Karthik
–
@Krishna Karthik
i want to play chess with Steven sir, but when i ask him that he plays chess?
He just ignored me.
Log in to reply
@Talulah Riley – Lol. I guess he's not the type of person for games.
Bro I can't chat 'cause I said shit in Chess
btw nice series of moves. You had the game :)
Log in to reply
@Krishna Karthik what thing bro? What shit in chess? I didn't understand?
Log in to reply
@Talulah Riley – I meant I typed "shit" into the chatbox lol
Log in to reply
@Krishna Karthik – @Krishna Karthik let's have a final match of 5min one more. This time no chatting only game.
Nice game bro. Good checkmate :)
Log in to reply
@Krishna Karthik How much matches dou you want to loose.??
Log in to reply
@Talulah Riley – Lmao yeah; I'm just not seeing good combinations of moves anymore. My chess brain is dead.
Simulating the dynamics by running a force computation routine is a nice way to attempt this problem.
In this kind of problem, there are two relevant components to each of these forces; tangential and normal. For that, I have calculated the unit tangent and normal vector of an ellipse:
t = b − a y i ^ + a b x j ^
t ^ = ∣ t ∣ t
n = a b x i ^ + b a y j ^
n ^ = ∣ n ∣ n
Normal forces
Normal reaction to gravity:
F g n ^ = m g cos ( θ ) n ^
Normal reaction to spring force:
F s n ^ = k ( 2 y − l ) cos ( θ ) n ^
Total normal force:
N = F g n ^ + F s n ^
Tangential forces
Ramp angle:
θ = tan − 1 ( d x d y )
Tangential gravitational force:
F g t ^ = m g sin ( θ ) t ^
Tangential spring force:
F s t ^ = k ( 2 y − l ) sin ( θ ) t ^
Friction force (occurs tangentially):
F μ t ^ = ± μ ∣ N ∣ t ^
Total tangential force
F t = F g t ^ + F s t ^ ± F μ t ^
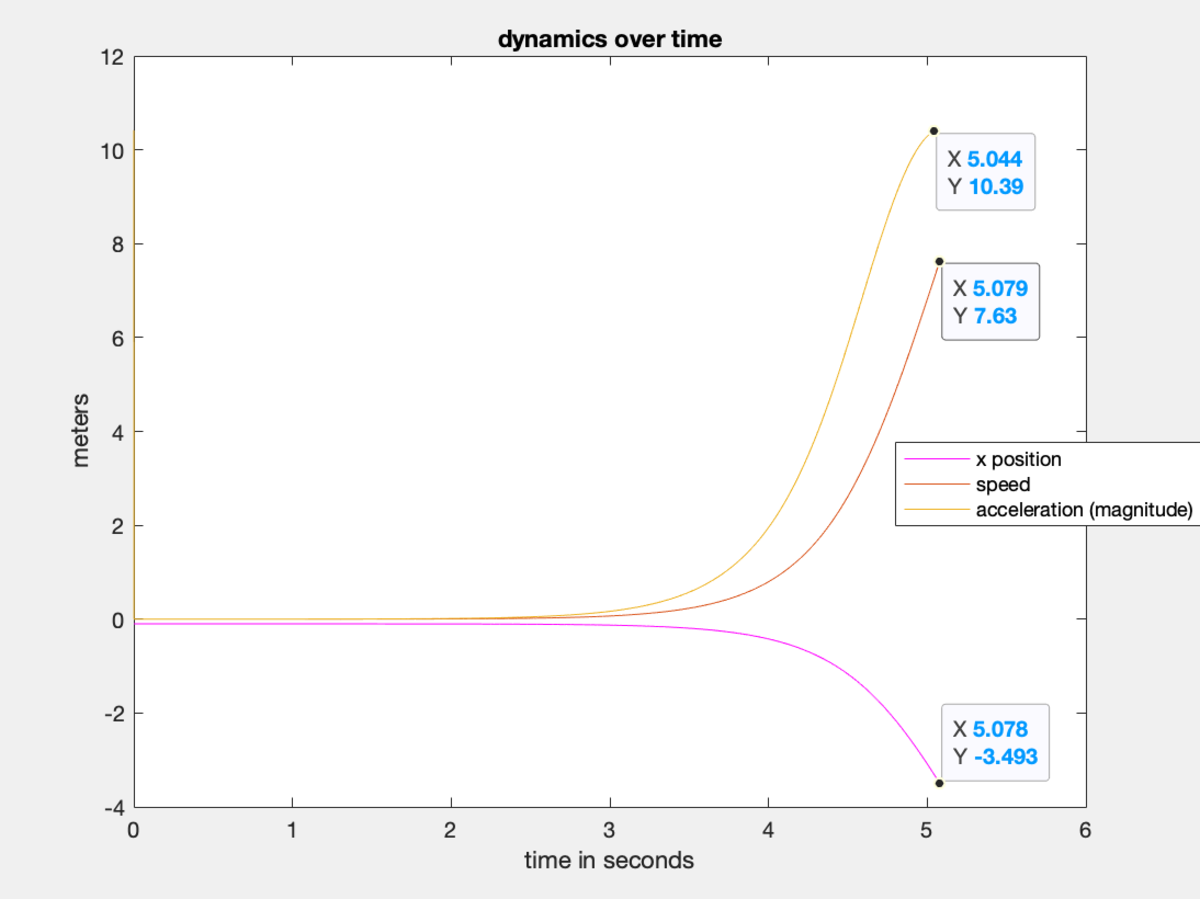
Simulation code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
|
@Krishna Karthik Bro what is the meaning of x 0 in the new problem??
Log in to reply
It means the initial length of the rope that's hanging
Hey; I like your method to solve the charges problem.
Log in to reply
@Krishna Karthik Let's have a chess match
Log in to reply
@Talulah Riley – I can't now; I'm going for piano class soon.
Log in to reply
@Krishna Karthik – @ @Krishna Karthik Ok no problem
@Krishna Karthik ok bro leave it, whatever you want to say, you are absolutely correct.
I got a bit different answer than what was expected (about 5 . 2 8 8 ). Let ( α , β ) = ( a 2 1 , b 2 1 ) . Derive an acceleration constraint equation.
α x 2 + β y 2 = 1 2 α x x ˙ + 2 β y y ˙ = 0 2 α x x ¨ + 2 α x ˙ 2 + 2 β y y ¨ + 2 β y ˙ 2 = 0
For convenience, I started the mass at x = + 0 . 1 and let it go until + 3 . 5 . Let u 1 be the unit normal vector, and let u 2 be a unit tangent vector opposite to the particle motion. For the sake of brevity, I will not derive these here. Let F g y and F s y be the vertical components of the gravity and spring forces. Write the Newton's 2nd law equations.
m x ¨ = N u 1 x + μ N u 2 x m y ¨ = N u 1 y + μ N u 2 y + F g y + F s y
Plugging these into the constraint equation and solving for the normal force yields:
N = 2 α x u 1 x + 2 α x μ u 2 x + 2 β y u 1 y + 2 β y μ u 2 y − 2 β y ( F g y + F s y ) − 2 α m x ˙ 2 − 2 β m y ˙ 2
Having solved for N , plug these back into the 2nd law equations to solve for the accelerations. Numerical integration takes care of the rest.
Solution code is attached.