SinCos Plus CosSin
sin ( cos x ) + cos ( sin x ) Find the minimum value of the above expression for x ∈ [ 2 − π , 2 π ] .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Can you please explain in detail.
Log in to reply
Sure, See this graph here (I am not able to upload an image for some reason): https://www.desmos.com/screenshot/1gxmxksj1e
Within the given domain, x ϵ [ 2 − π , 2 π ]
the function attains a maxima at x=0 (which can be found by taking the derivative and equating it to zero) and the lowest value f(x) can take in the given interval is at the end points of the interval itself (as there is no other extrema in the domain), in such a case, we can substitute the values of the end-points in the original equation to see which one gives a lower value, in the given question, both the end-points, namely [ 2 − π , 2 π ] give the same result (as the function is symmetric) which is cos1
Log in to reply
Sorry I will be asking a DUMB question- What if we do not know the graph. Then how can we predict that function is symmetrical or it has maximum/minimum at end points of given domain. Also taking derivative of expression we get sin ( sin x ) × cos x + cos ( cos x ) × sin x = 0 . How to find find its roots (without value putting , of course)
Log in to reply
@Neelesh Vij – For this question, we need not know if the graph is symmetrical, it just turns out to be symmetrical.
Finding the roots of this equation without value putting is not very easy, I don't know the exact method but I think we can write sin(sinx) as 2 1 i e 2 e − i x − e i x − 2 1 i e 2 e i x − e − i x = 0
and sin(sinx)cosx as 4 1 i ( e 2 e − i x − e i x − e 2 e i x − e − i x ) ( e − i x + e i x ) = 0
Similarly cos(cosx)sinx can be written as 4 1 i ( e 2 − ( e − i x + e i x ) + e 2 e − i x + e i x ) ( e − i x − e i x ) = 0 using Euler's form of complex numbers We add them, equate it to zero and solve
But, in this problem, the better way would be to try substituting values for which the derivative becomes zero. For the given domain, we observe that it becomes zero for x=0 and there is no other point of extrema anywhere else, so the other extreme possibilities is at the end-points, as the function would be either decreasing or increasing for all values between the end-points and the point of extrema, so there cannot be a possibility of any other extreme value in between.
Thus, we check for the end-points too, and the minima will be the lowest value obtained among the three concerned points. There may be points in the graph where we can obtain yet lower values outside the given domain but we are concerned only about our domain.
If you are preparing for the JEE, I would suggest practising curve sketching as it is very useful in a wide variety of problems. Hope this helps... This wasn't a dumb question at all :)
Log in to reply
@Aman Deep Singh – Now i get it. Thanks for explanation P.S. Yes i am preparing for JEE 2017
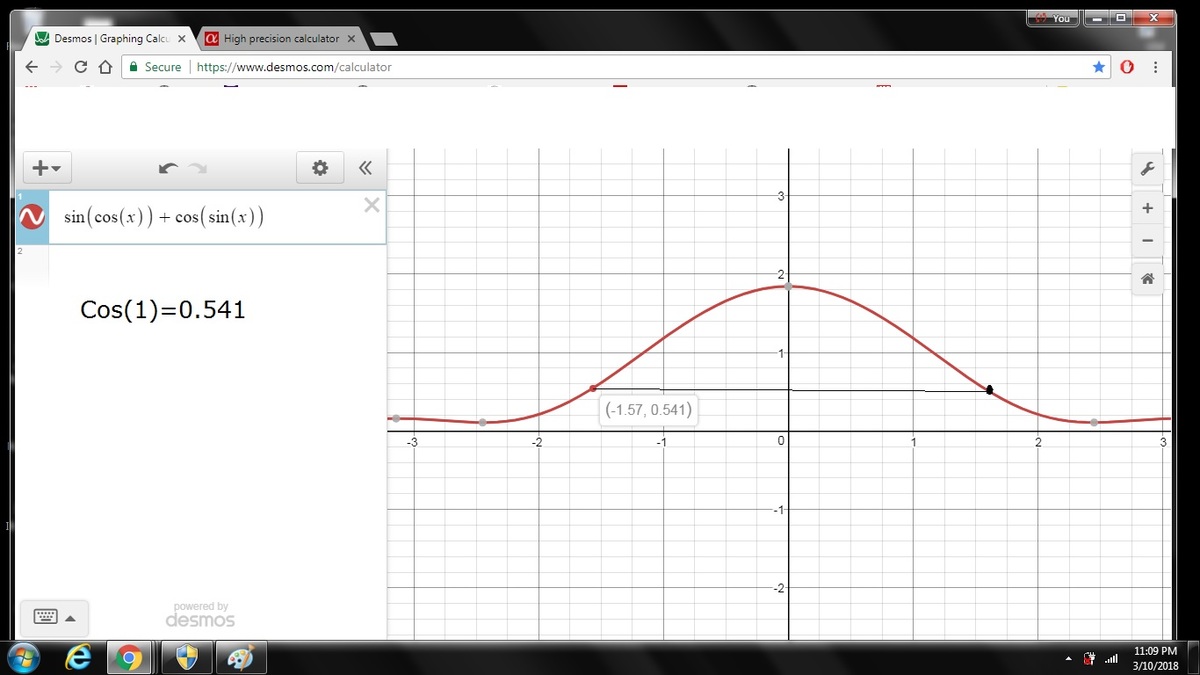
@Aditya Kumar In the given domain, maxima occurs when x=0, there is no other point in the domain for which the derivative is zero, therefore, minimum value occurs at either of the end points of the domain. In this case, f ( 2 π ) = f ( 2 − π ) = cos 1
Your answer is correct but your reasoning is wrong :) Edit: now I see you have pulled down your solution :)