Sine Wave Sliding
A massive bead slides on a smooth wire in the shape of the curve y = s i n ( x ) . The wire is fixed in place, and it extends infinitely in the + x and − x directions. Gravity ( g ) is 1 0 m/s 2 in the − y direction.
At time t = 0 , the x position and velocity are:
x 0 = 0 x ˙ 0 = + 0 . 9 5 g
What is the first time (after t = 0 ) at which the x position and velocity simultaneously match their initial values?
Note: Assume that everything is in standard SI units (ignore the apparent x ˙ 0 dimensionality mismatch)
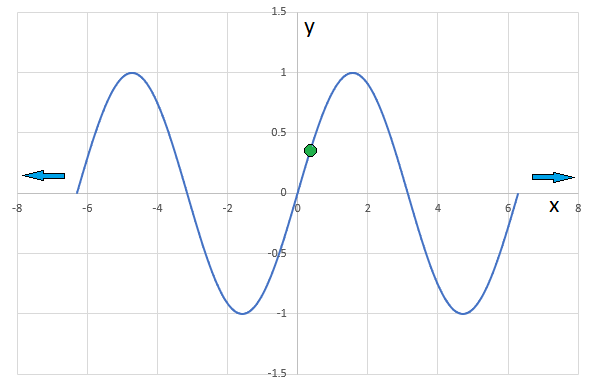
The answer is 4.5036.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Steven Chase are you online ,I want to discuss something with you ?
Log in to reply
Yes, you can ask
Log in to reply
I have think of more than 10 ideas to start my business within 6 months in college.
One of my ideas is you know about Starbucks they offer coffee of such a high price ,.
Can I start a business like this specially for Tea ,what do you think ,?
Log in to reply
@Talulah Riley – It's a good idea to make some money to get yourself through school. Most people do this by being an employee of a company and working part time (maybe 20 hours a week) while in school. Starting a business while in school could be very challenging, depending on the scale of the business. How much money are you hoping to bring in every year with this business?
Log in to reply
@Steven Chase
–
@Steven Chase
Feeling good after seeing someone showing interest in my ideas .
When I told these ideas to my mother and Father they use to say focus on your studies ..
I am taking admission in university not in school.
I am not hoping to bring any money ,just FOCUSING on solving problem of people.
@Steven Chase
You know
Ritesh Agarwal
.
He became billionaire at just age of 24 ,he always says ,focus on the problem of people not on money.
@Steven Chase why are you so quiet?say something?
Log in to reply
I don't have much business advice to give, since I have never started one myself. But good luck
Log in to reply
@Steven Chase It is never too late .I suggest you to start your bussiness as early as possible.
@Steven Chase
The moment I got some good money from my business.
I will start a electric vehicles company .In future there will be good craze for electric vehicle in India to beat Tesla
@Steven Chase At first Vehicles use to run with Coal,after that Diesel/gas/Petrol after that Electricity after that what will come ???
Animal power (horses, oxen, etc.) came even before coal. I think electricity will be the final form of propulsion for cars.
Log in to reply
@Steven Chase
Haha ,everyone knows that Animal power came first .
You are not a creator of universe.you are just a living organism in Earth.
So you can't say so confidentally that Electricity will be the final form.
I am damn sure something will come more cheaper,more comfortable,more effecient than electric cars.
And Neeraj is the guy who will invent that .Bye :).
@Steven Chase Do you have a Tesla car ???
@Steven Chase what is the company of your car ?
@Steven Chase why you are so quiet again?say something?
By the conservation of energy, x ˙ 2 + y ˙ 2 + 2 g y = x ˙ 0 2 + y ˙ 0 2 = x ˙ 0 2 + ( y ′ ( x 0 ) ) 2 x ˙ 0 2 = 2 x ˙ 0 2 = 2 ( 0 . 9 5 2 g ) Here, we note that this gives y = 0 . 9 5 2 < 1 when the velocity is zero, so the bead won't escape from between the two peaks at x = − 2 3 π , 2 π .
Between these two peaks, x = sin − 1 ( y ) or x = − 2 π − sin − 1 ( y ) , so we have x ˙ = ± 1 − y 2 1 y ˙ , and the above equation becomes 1 − y 2 1 y ˙ 2 + y ˙ 2 + 2 g y = 2 ( 0 . 9 5 2 g ) ⟹ ( ( 1 − y 2 ) ( 0 . 9 5 2 − y ) 2 − y 2 ) y ˙ = ± 2 g
Now, if the position and velocity first match their initial values at time t = T , then T will be the time period for the movement of the bead. By the symmetry in the graph about the low point at x = − 2 π and the symmetry in the time axis, we conclude that it takes 4 T for the bead to move from the low point at y = − 1 to its highest point at y = 0 . 9 5 2 . If we suppose that the bead is at y = − 1 at t = t l o w , then we can integrate the equation we found: ∫ − 1 0 . 9 5 2 ( 1 − y 2 ) ( 0 . 9 5 2 − y ) 2 − y 2 d y = ∫ t l o w t l o w + 4 T 2 g d t = 4 T 2 g and solving for T gives T = 2 g 4 ∫ − 1 0 . 9 5 2 ( 1 − y 2 ) ( 0 . 9 5 2 − y ) 2 − y 2 d y ≈ 4 . 5 0 3 5 6 6 1 8 7 5 4 9 4
See the energy-based solution from @Brian Moehring , in which he goes into detail about the constraints on the bead's motion, and about the computation of the final answer. The only thing I will add here is an alternate Lagrangian solution for the second-derivative of x . The resulting expression can be numerically integrated to get the solution. This results in a list of ( t , x , y ) coordinates which describes the particle trajectory.
Positions and velocities:
x = x y = s i n ( x ) x ˙ = x ˙ y ˙ = c o s ( x ) x ˙
Kinetic Energy:
E = 2 1 m ( x ˙ 2 + y ˙ 2 ) = 2 1 m x ˙ 2 [ 1 + c o s 2 ( x ) ]
Potential Energy:
U = m g y = m g s i n ( x )
Lagrangian:
L = E − U = 2 1 m x ˙ 2 [ 1 + c o s 2 ( x ) ] − m g s i n ( x )
Equation of Motion:
d t d ∂ x ˙ ∂ L = ∂ x ∂ L
Inner left side:
∂ x ˙ ∂ L = m x ˙ [ 1 + c o s 2 ( x ) ]
Left side:
d t d ∂ x ˙ ∂ L = m x ˙ [ − 2 s i n ( x ) c o s ( x ) x ˙ ] + m x ¨ [ 1 + c o s 2 ( x ) ]
Right side:
∂ x ∂ L = 2 1 m x ˙ 2 [ − 2 s i n ( x ) c o s ( x ) ] − m g c o s ( x )
Equating left and right sides:
− 2 x ˙ 2 s i n ( x ) c o s ( x ) + x ¨ [ 1 + c o s 2 ( x ) ] = − x ˙ 2 s i n ( x ) c o s ( x ) − g c o s ( x ) x ¨ [ 1 + c o s 2 ( x ) ] = x ˙ 2 s i n ( x ) c o s ( x ) − g c o s ( x )
Final result:
x ¨ = 1 + c o s 2 ( x ) x ˙ 2 s i n ( x ) c o s ( x ) − g c o s ( x )