Sinusoidal Wire Magnetics (part 2)
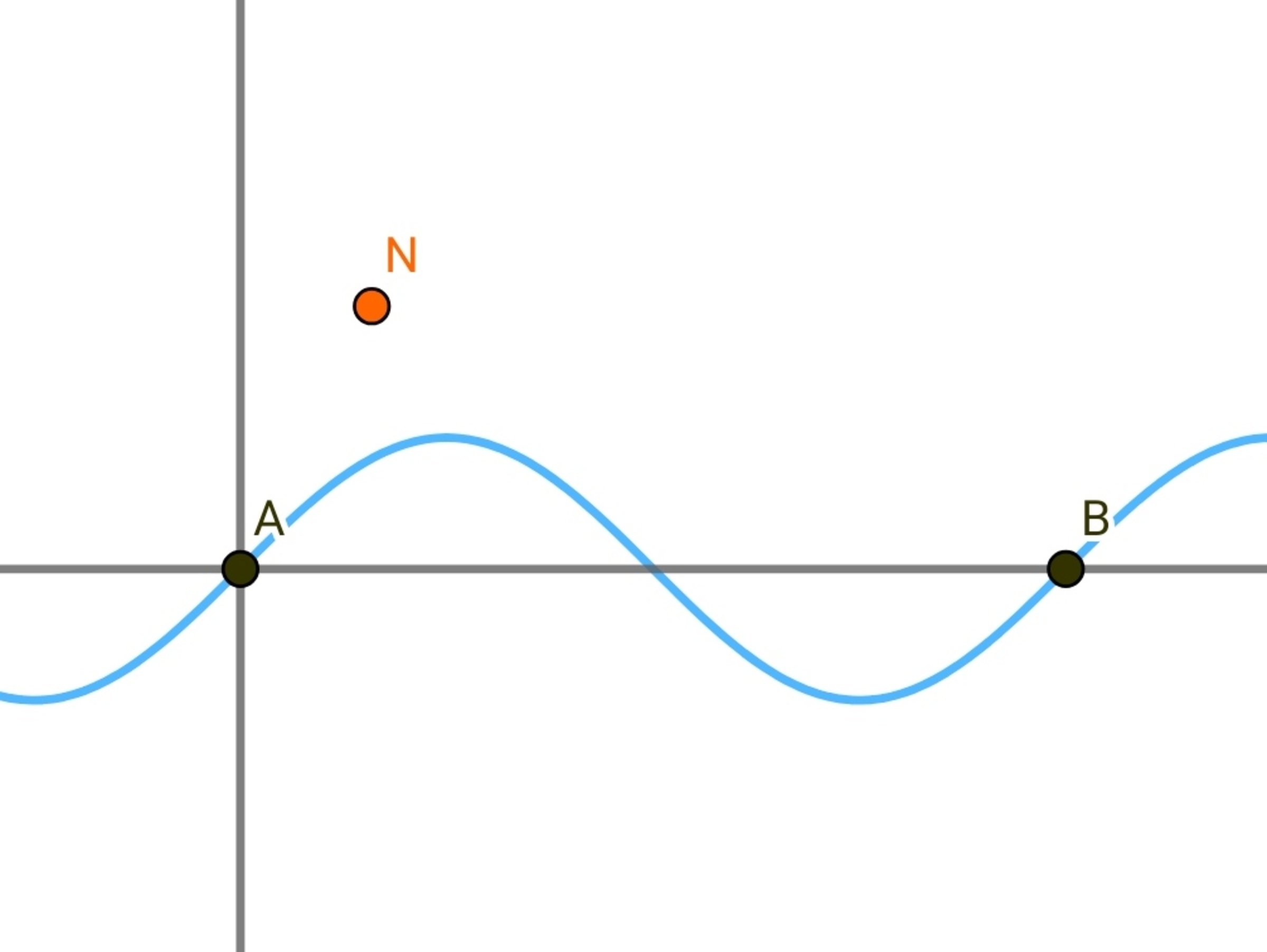
A piece of wire has the following shape
0
≤
x
≤
2
π
,
y
=
s
i
n
x
,
z
=
0
from position
A
to
B
. The wire carries a current of
I
=
4
π
A
. What is the magnitude of the magnetic flux density
B
at test point
N
(
x
,
y
,
z
)
=
(
1
,
2
,
3
)
Details and Assumptions 1) Magnetic permeability μ 0 = 1 .
The answer is 0.315.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Very nice problem:
Consider a point on the wire having a position vector:
r p = x i ^ + sin x j ^ + 0 k ^
The point of interest is:
r c = 1 i ^ + 2 j ^ + 3 k ^
A vector joining these two points directed towards the point of interest is:
r = r c − r p
The current is assumed to flow rightwards along the sine curve. An arc length element vector along the curve is:
d s = ( 1 i ^ + cos x j ^ + 0 k ^ ) d x
From here, Biot-Savart Law is applied, which is:
d B = 4 π μ o I ∣ r ∣ 3 d s × r
Substituting and simplifying gives the expressions:
d B = d B x i ^ + d B y j ^ + d B z k ^
Where:
d B x = ( ( x − 1 ) 2 + ( sin ( x ) − 2 ) 2 + 9 ) 3 / 2 3 cos ( x ) d x d B y = − ( ( x − 1 ) 2 + ( sin ( x ) − 2 ) 2 + 9 ) 3 / 2 3 d x d B z = ( ( x − 1 ) 2 + ( sin ( x ) − 2 ) 2 + 9 ) 3 / 2 ( cos ( x ) ( x − 1 ) − sin ( x ) + 2 ) d x
Finally:
B x = ∫ 0 2 π ( ( x − 1 ) 2 + ( sin ( x ) − 2 ) 2 + 9 ) 3 / 2 3 cos ( x ) d x B y = ∫ 0 2 π − ( ( x − 1 ) 2 + ( sin ( x ) − 2 ) 2 + 9 ) 3 / 2 3 d x B z = ∫ 0 2 π ( ( x − 1 ) 2 + ( sin ( x ) − 2 ) 2 + 9 ) 3 / 2 ( cos ( x ) ( x − 1 ) − sin ( x ) + 2 ) d x
The net magnetic field at the point of interest is:
B = B x i ^ + B y j ^ + B z k ^
And the required magnitude is:
∣ B ∣ = B x 2 + B y 2 + B z 2 ≈ 0 . 3 1 5 4
@Karan Chatrath your B x = − B x and for also y and z axis I got values. Well, I don't know why this is happening . I know while it doesn't matter because we have to do square. But opposite sign is coming in my solution. Can you tell me why??
Log in to reply
Check your sign convention for current. And see how I defined r . Maybe the difference is there.
Also, I must say that I admire your creativity in posting problems. I enjoy the questions. You can even think of questions other than E&M. Maybe try mechanics (gravitation, moment of inertia of complex volumes, kinetics).
Log in to reply
Thankyou sir. Sir I have taken r = r p − r c but when the direction of current is given in the question then it will effect the expression. Am I right??
Log in to reply
Yes, the current direction has an effect on the field direction
Log in to reply
@Karan Chatrath – @Karan Chatrath the latest question which you reported I just want to know in which direction you are getting forces . Will the forces in + Y and + Z axis be zero??
Log in to reply
@A Former Brilliant Member
–
@Karan Chatrath I have made a big assumption that only in x direction force will be there. Is it correct . Here I have attached my solution.
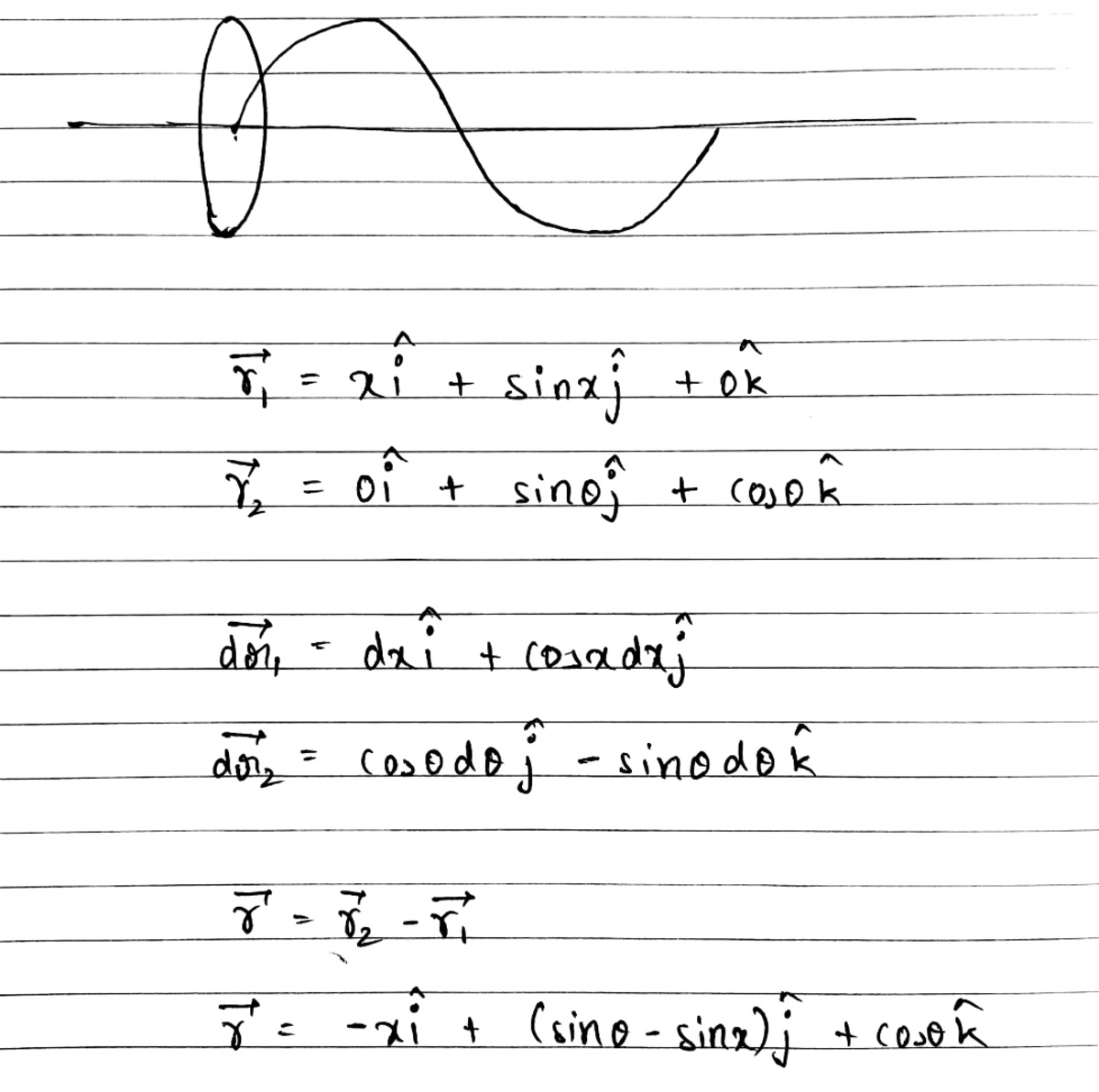

Log in to reply
@A Former Brilliant Member – @Karan chatrath that F − x direction force is the answer.
@A Former Brilliant Member – Recheck your expression for d F x . Also, I get force along X as zero. The net force is along Z. Wolfram should not fail to calculate the last integral.
I checked the answer using code also.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
I again rechecked my equation and it's coming the same. No mistake encountered.
F
x
 F
y
F
y
 F
z
F
z
 This type of unsual things come when I write integrals correctly with proper limits. Only wolfram is showing
F
x
This type of unsual things come when I write integrals correctly with proper limits. Only wolfram is showing
F
x
Log in to reply
@A Former Brilliant Member – Expression that I get for d F x :
d F x = − ( cos ( θ ) 2 + x 2 + ( sin ( x ) − sin ( θ ) ) 2 ) 3 / 2 cos ( θ ) ( sin ( x ) − x cos ( x ) ) d θ d x
Log in to reply
@Karan Chatrath – @Karan Chatrath Ok i will solve the question from starting again . While in the mean time can you find mistake in solution?? Please
Log in to reply
@A Former Brilliant Member – Mistake should be when you compute d B . That expression looks odd to me.
Log in to reply
@Karan Chatrath – Ok sir I have check several times. can you post your solution from starting as I have posted??
Log in to reply
@A Former Brilliant Member – It will take it too long to type, besides, I do not type the steps in between. Maybe much later, I can. Also, check your expression for \dB z .
Log in to reply
@Karan Chatrath – I think that while calculating the cross product in the d B expression, you have made an error. I have verified my answer with code also.
Log in to reply
@Karan Chatrath – You do not need to type just click photo of your whole solution and paste it . It will help me a lot. It will not take more than 5 min . Please
Log in to reply
@A Former Brilliant Member – I am sorry, I do not have that notepad with me. I would have to write it all over.
Log in to reply
@Karan Chatrath – @Karan Chatrath sir write the solution in page and click photo and paste it here
Log in to reply
@A Former Brilliant Member
–
Finally I find the mistake. You were correct the mistake is in
d
B
 After correcting the mistake ,i get the forces as
After correcting the mistake ,i get the forces as
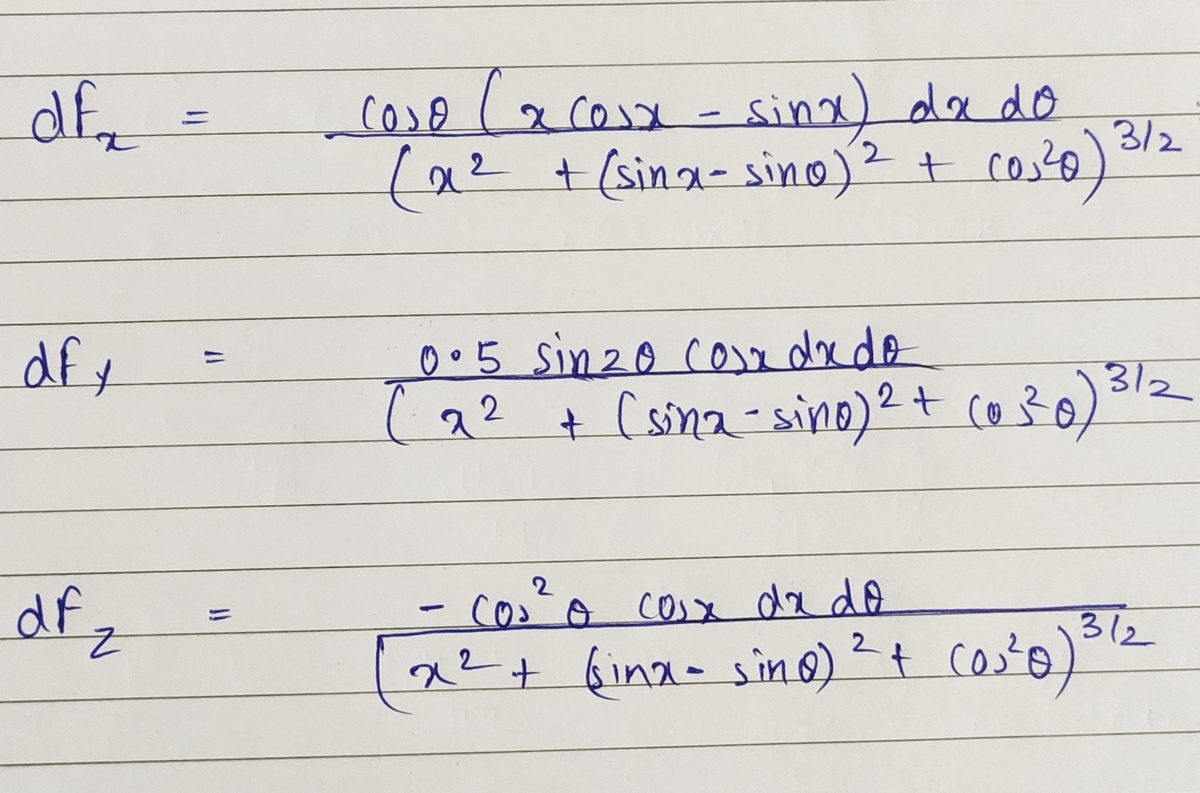
@Karan Chatrath
Please sir can you help me this time. As you have earlier said I have to do calculations very carefully but also this time my answer is coming wrong of the new question solenoid exercise. Here is my solution. Can you find the mistake



Log in to reply
The mistake you are making is that you are calculating turns per unit length, etc. You do not need to treat the problem this way. Normally, the reason why we approach the problem by calculating turns per unit length is that the curve of the solenoid is not exactly parameterised. In this problem, an exact parameterisation of the solenoid is given. Treat this just as any other Biot-Savart law exercise. The resulting integral you obtain should be a single integral.
Nevertheless, your answer is close to the correct value.
Log in to reply
@Karan Chatrath – Thank you sir very much. Sir but my 1 try is left and i want to upload the solution. Can you tell me how can i take a random point on that solenoid??? Please tell that random point after that i will definitely post a very beautiful solution.
Log in to reply
@A Former Brilliant Member – A point on the solenoid:
r p = cos θ i ^ + sin θ j ^ + ( − 1 0 + 1 0 0 π θ ) k ^ d r p = ( − sin θ i ^ + cos θ j ^ + ( 1 0 0 π 1 ) k ^ ) d θ
The second vector is an elementary arc-length vector tangential to the point on the solenoid.
Log in to reply
@Karan Chatrath – @Karan Chatrath Thankyou sir very much.
@Karan Chatrath
–
@Karan Chatrath
I am still getting my answer which i tried in my second try. Therefore my third try is still remaining. I checked several times this solution which I solved by your method. Can you find the mistake.???
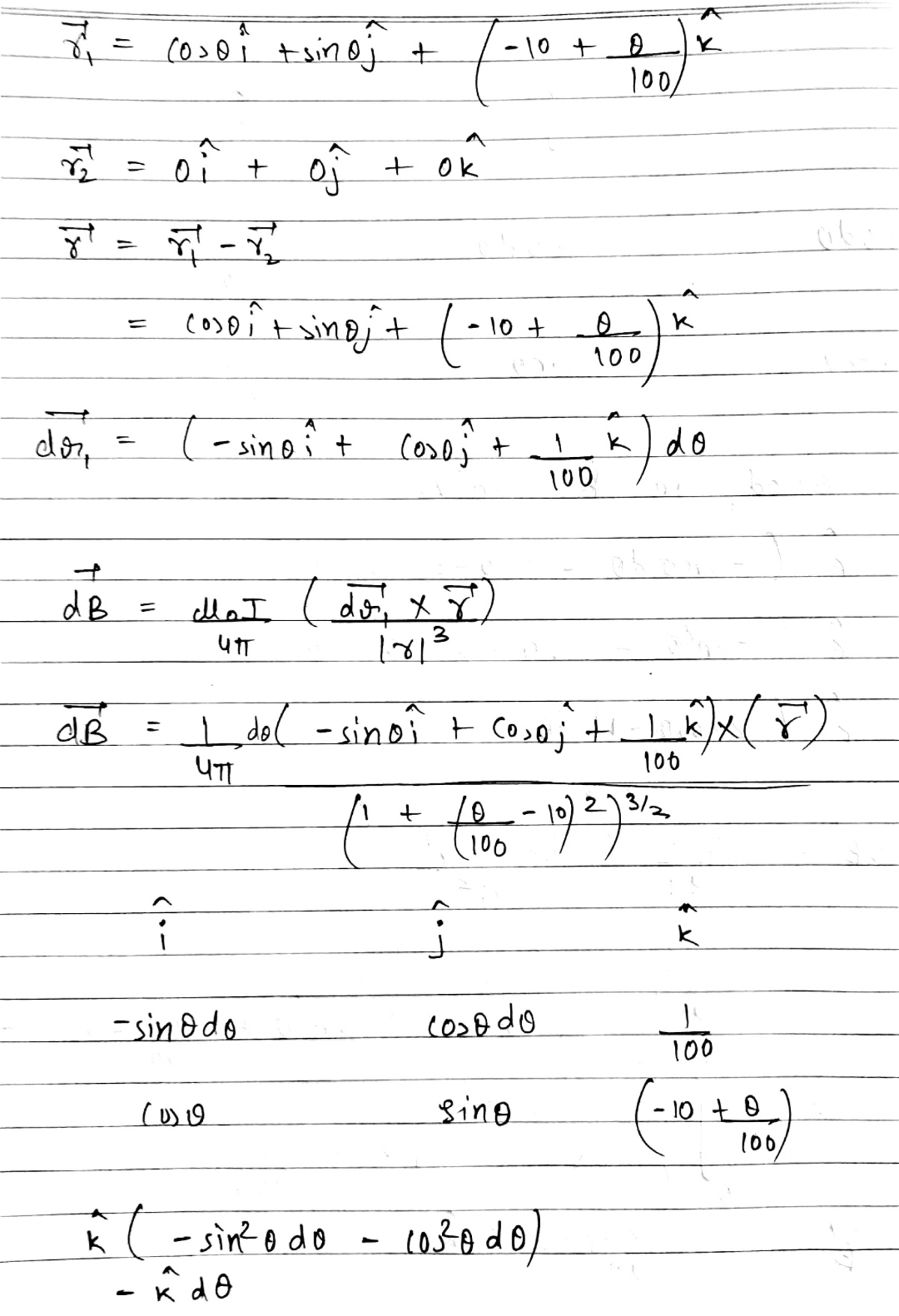
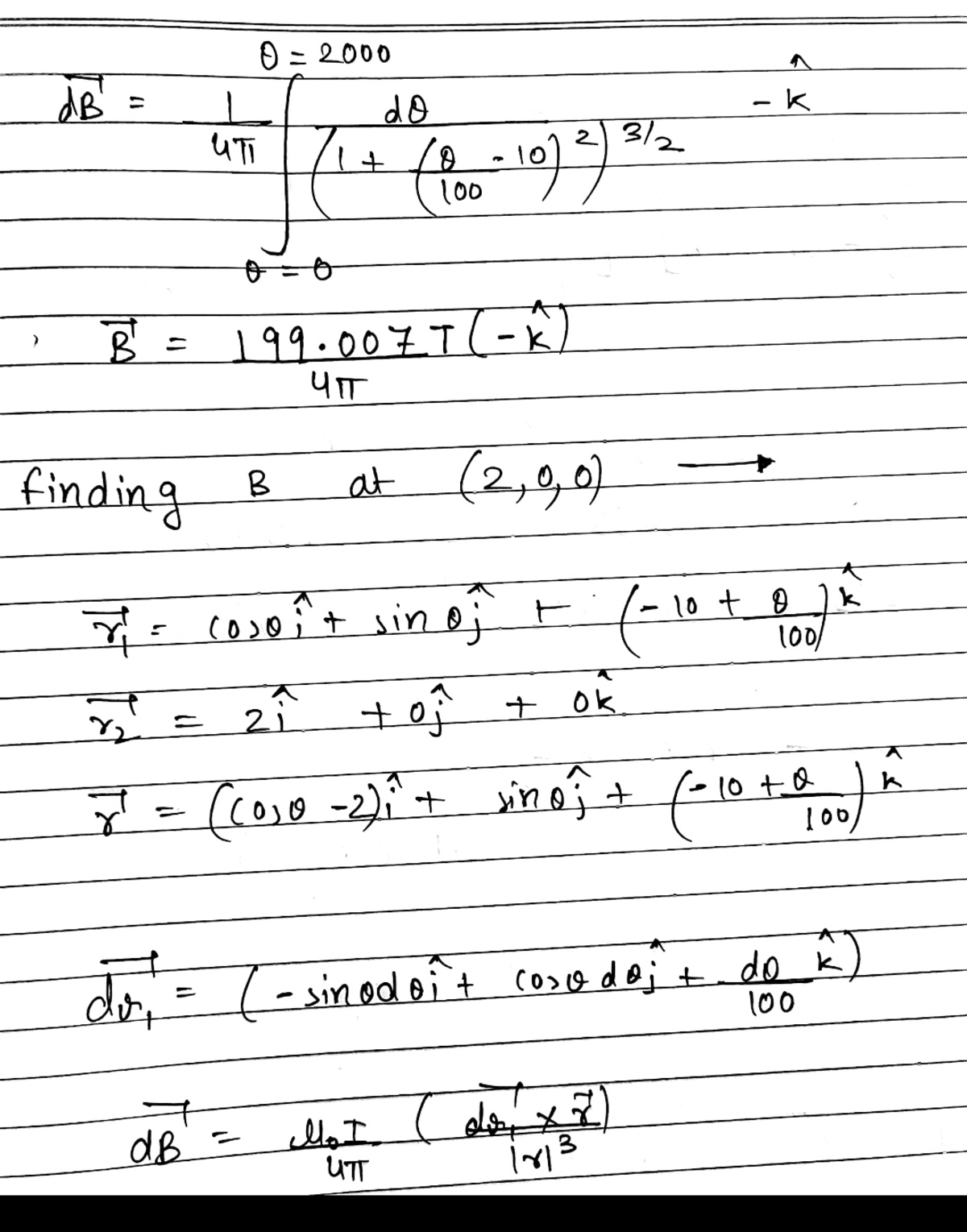

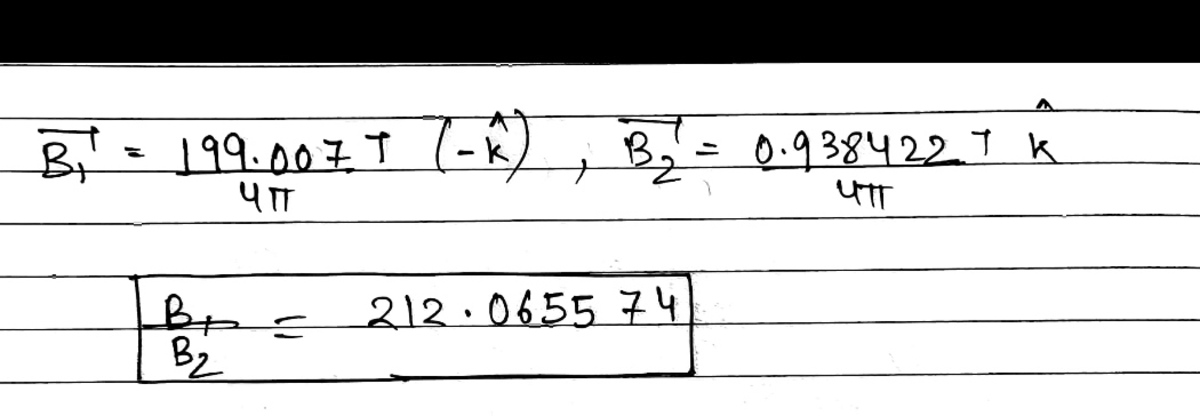
Log in to reply
@A Former Brilliant Member – You are integrating from 0 to 2000. You must integrate from 0 to 2 0 0 0 π . Re-read the question carefully
Log in to reply
@Karan Chatrath – @Karan Chatrath Sir if I integrate it from 0 to 2000π then according to the limit the height of the cylinder is 20π but the height of cylinder is 20??.And Sir I want to ask one more thing which I forgot to ask is that in your expression of r p in the k part it should be − 1 0 + 1 0 0 π θ
Log in to reply
@A Former Brilliant Member – Yes, you are right: It should be:
r p = cos θ i ^ + sin θ j ^ + ( − 1 0 + 1 0 0 π θ ) k ^ d r p = ( − sin θ i ^ + cos θ j ^ + ( 1 0 0 π 1 ) k ^ ) d θ
@Karan Chatrath
–
@Karan Chatrath
After putting the limits correctly I am still getting my answer as
B
2
B
1
=
2
1
2
.
4
4
2
For
B
1
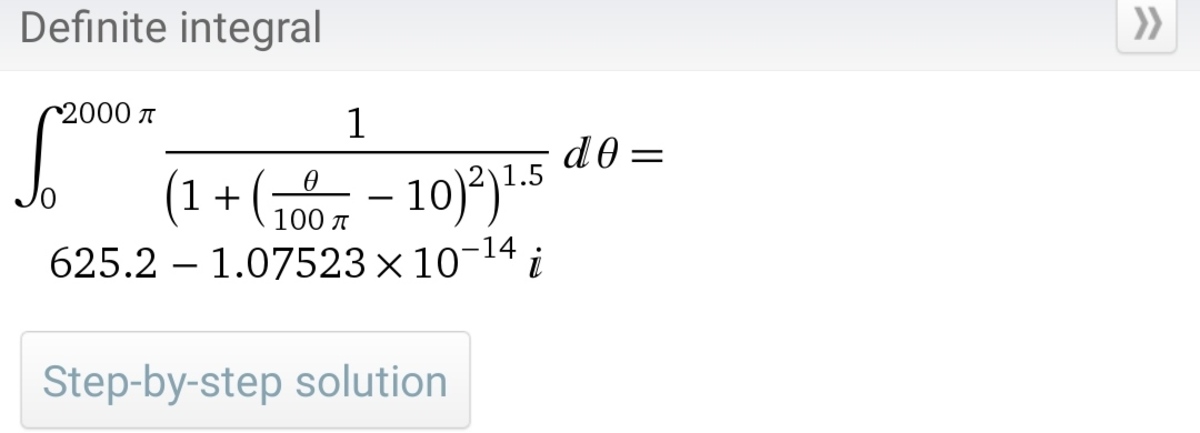 For
B
2
For
B
2
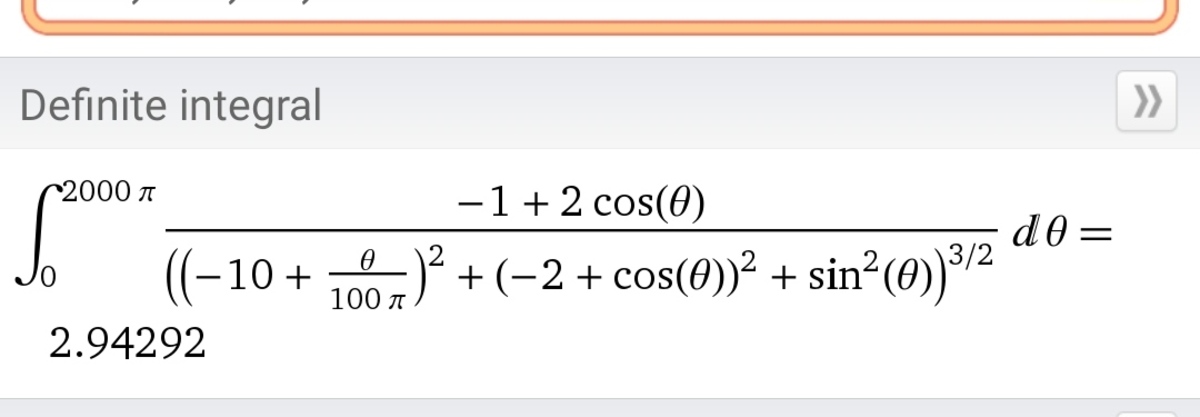
Log in to reply
@A Former Brilliant Member – Calculate all the components of the magnetic field. Other components are not zero.
Log in to reply
@Karan Chatrath – Also, please check your calculations carefully. That I have not done.
Log in to reply
@Karan Chatrath – @Karan Chatrath ok sir Thank you, sir but it's very starnge that magnetic field has components also . Well I was assuming that it will be only in k direction.
@Karan Chatrath . Is wolfram giving answers of F x , F y . In my wolfram it is not giving.
Log in to reply
Well done. Glad you found the error. To answer your question, no, Wolfram does not evaluate those integrals. I solved them using code and noticed that they are both zero. I think your result for F z should be similar to what I obtain, now
Log in to reply
Yes sir it's similiar. Thankyou
Log in to reply
@A Former Brilliant Member – @Karan chatrath I have reposted the question
Log in to reply
@A Former Brilliant Member – https://brilliant.org/problems/infinite-wire-magnetics/ please can you post the solution of this question . Code bhi chalega.