Sinusoidal Wire Magnetics (part 3 )
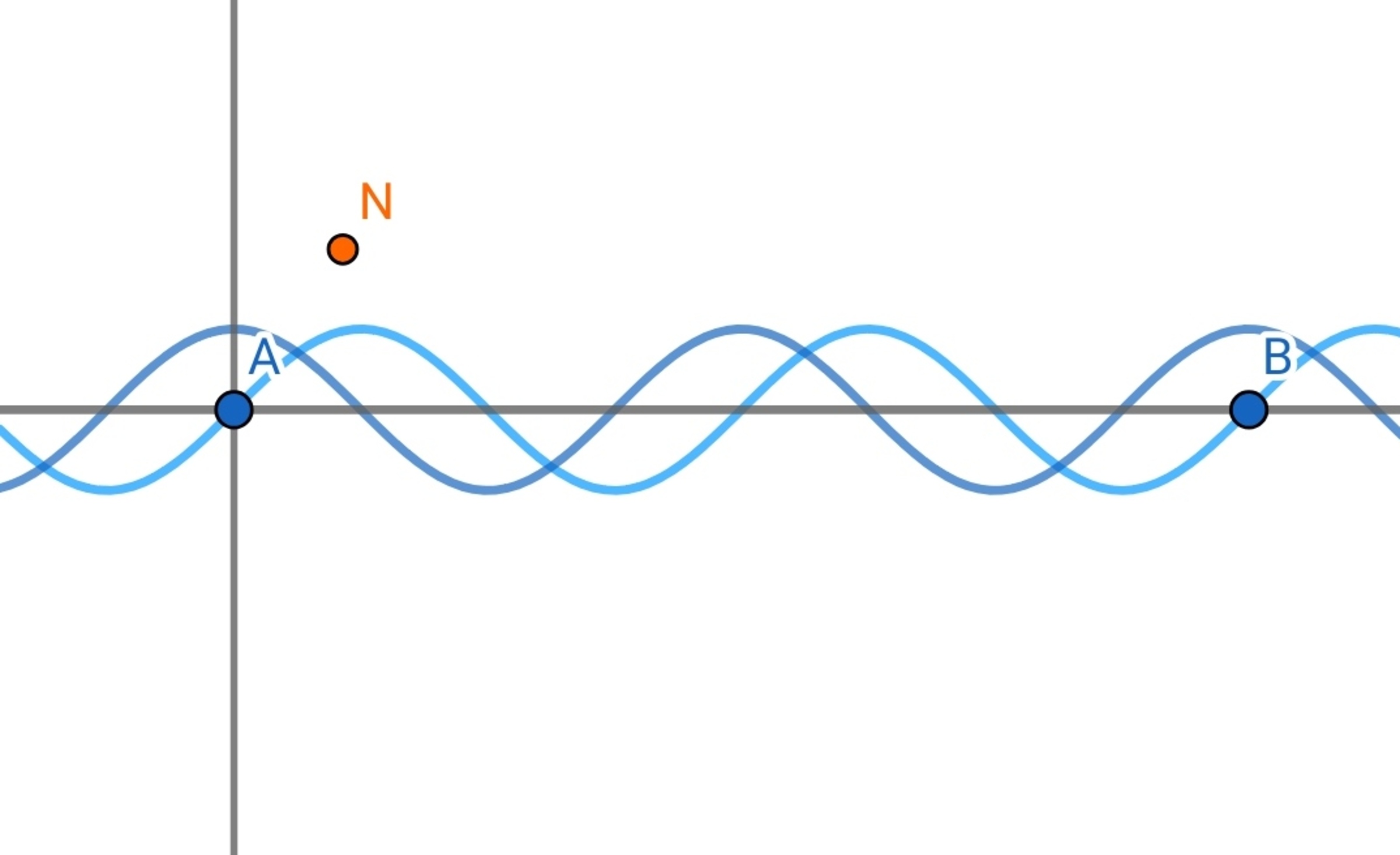
A piece of wire has the following shape
0
≤
x
≤
4
π
,
y
=
sin
x
,
z
=
0
from position
A
to
B
upto two cycle. There is one more wire of the following shape
0
≤
x
≤
4
π
,
y
=
cos
x
,
z
=
1
from position
A
to
B
upto two cycle. Both the wire carries a current of
4
π
A
. What is the magnitude of net magnetic field
B
n
e
t
at test point
N
(
x
,
y
,
z
)
=
(
1
,
2
,
3
)
 Details and Assumptions
1) Magnetic permeability
μ
0
=
1
Details and Assumptions
1) Magnetic permeability
μ
0
=
1
The answer is 0.847.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Karan Chatrath The questions which you reported today. Current circulate around the center . For solving this question you can take a element at a distance x then multiply element's area with current per unit area in the whole disk.
Log in to reply
Thank you for the clarification
Log in to reply
Problem solved, report deleted
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
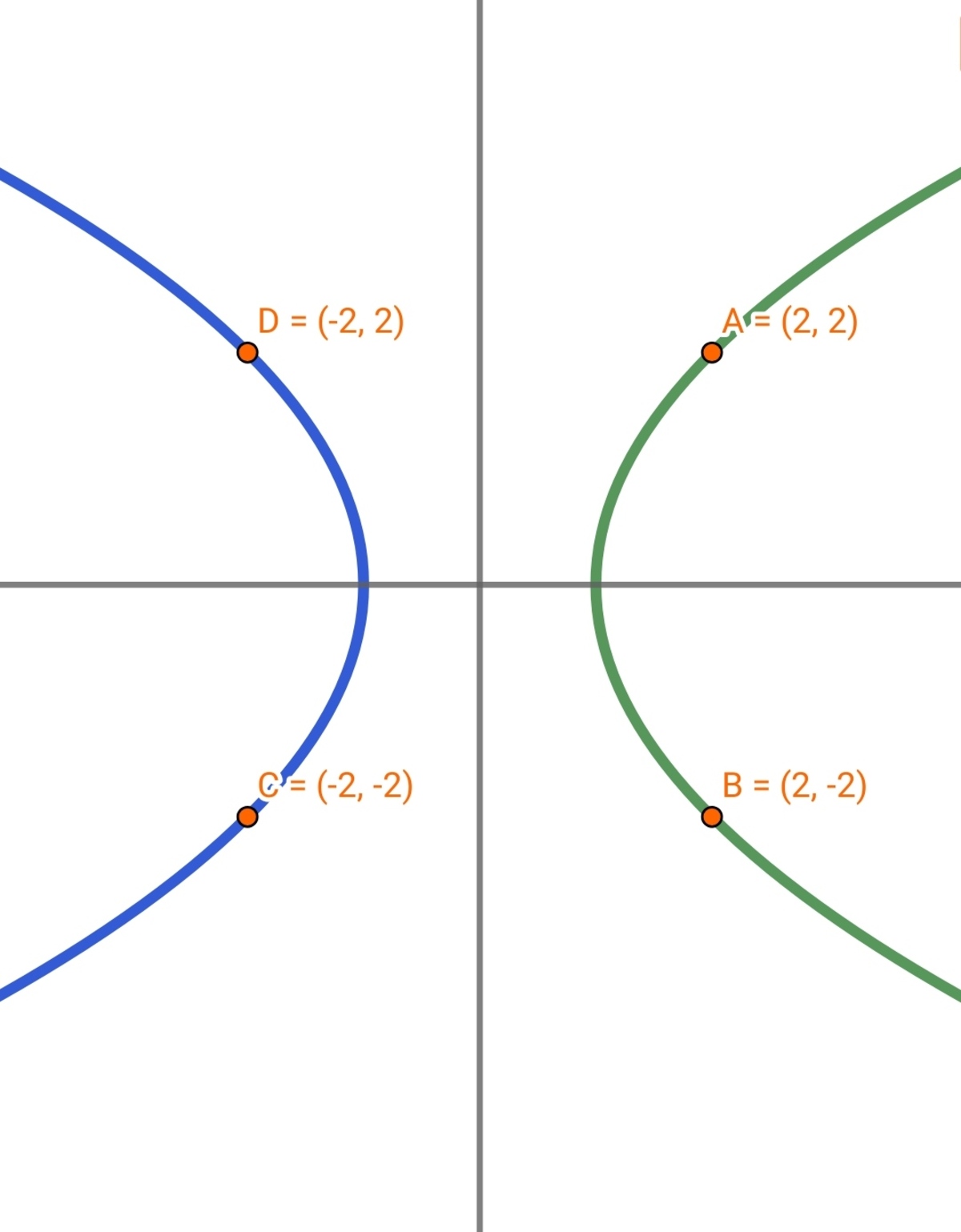
Sir was making a question yesterday. But i can't. I think wolfram is not capable of doing that high level integration. The question is that. We have to find magnetic force between segment AB and CD .Can you help me? .Two parabolas of equation
y
2
=
4
(
x
−
1
)
y
2
=
−
4
(
x
+
1
)
Log in to reply
@A Former Brilliant Member – @Karan Chatrath The comment has been edited.
Log in to reply
@A Former Brilliant Member – I am able to perform the integral for F x using Wolfram. Verified result using code. Assuming that μ o = 1 and that each wire carries a current of I = 2 π , I get the net force as:
F x ≈ 1 . 5 4 1 5 1 F y = F z = 0
The expression for d F x is:
d F x = ( 1 6 ( y 1 − y 2 ) 2 + ( y 1 2 + y 2 2 + 8 ) 2 ) 3 / 2 1 6 ( − y 1 2 + 2 y 1 y 2 + y 2 2 + 8 ) d y 1 d y 2
F x = ∫ − 2 2 ∫ − 2 2 ( 1 6 ( y 1 − y 2 ) 2 + ( y 1 2 + y 2 2 + 8 ) 2 ) 3 / 2 1 6 ( − y 1 2 + 2 y 1 y 2 + y 2 2 + 8 ) d y 1 d y 2
y 1 is the Y-coordinate for the right parabola while y 2 is the y-coordinate for the left parabola.
Log in to reply
@Karan Chatrath – @Karan Chatrath Thanks Sir this time you have taken element by going y distance in Y axis. You don't want to go and take element in x axis to avoid square root? Am I correct
Log in to reply
@A Former Brilliant Member – That is correct
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
Sir help me in this integral. Making very interesting question
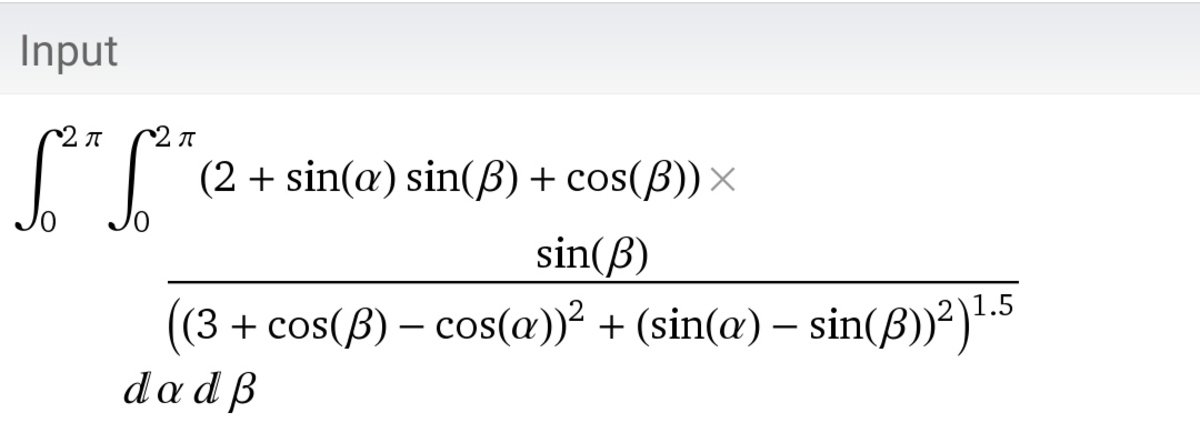 .
.
Log in to reply
@A Former Brilliant Member – I think it evaluates to zero
@Karan Chatrath Sir I am rechecking the question I get F x = 0 . 4 9 7 . Can you check it with code ,in the mean time I am trying to achieve F x = 0 . 6 2 2
Log in to reply
@A Former Brilliant Member – I have checked with code as well.
Log in to reply
@Karan Chatrath – Ok sir fine within 30 min I will change the question
Log in to reply
@A Former Brilliant Member – No, before doing so, find the source of a mistake if any. Don't ever rule out the possibility that I might be wrong.
Log in to reply
@Karan Chatrath
–
 finally I reached this expression,but wolfram is not giving answer and it's not matching with your expression which you have written in your report.
finally I reached this expression,but wolfram is not giving answer and it's not matching with your expression which you have written in your report.
Log in to reply
@A Former Brilliant Member – Well, it is quite similar to what I reported apart from a negative sign for one of the terms in the numerator. Please re-check your work. Also, Wolfram evaluates that expression that you have got. It evaluates to approximately 6.1.
You may paste the snapshots of your work here, if you want.
@Karan Chatrath
–
@Karan chatrath I have taken left circle center as origin


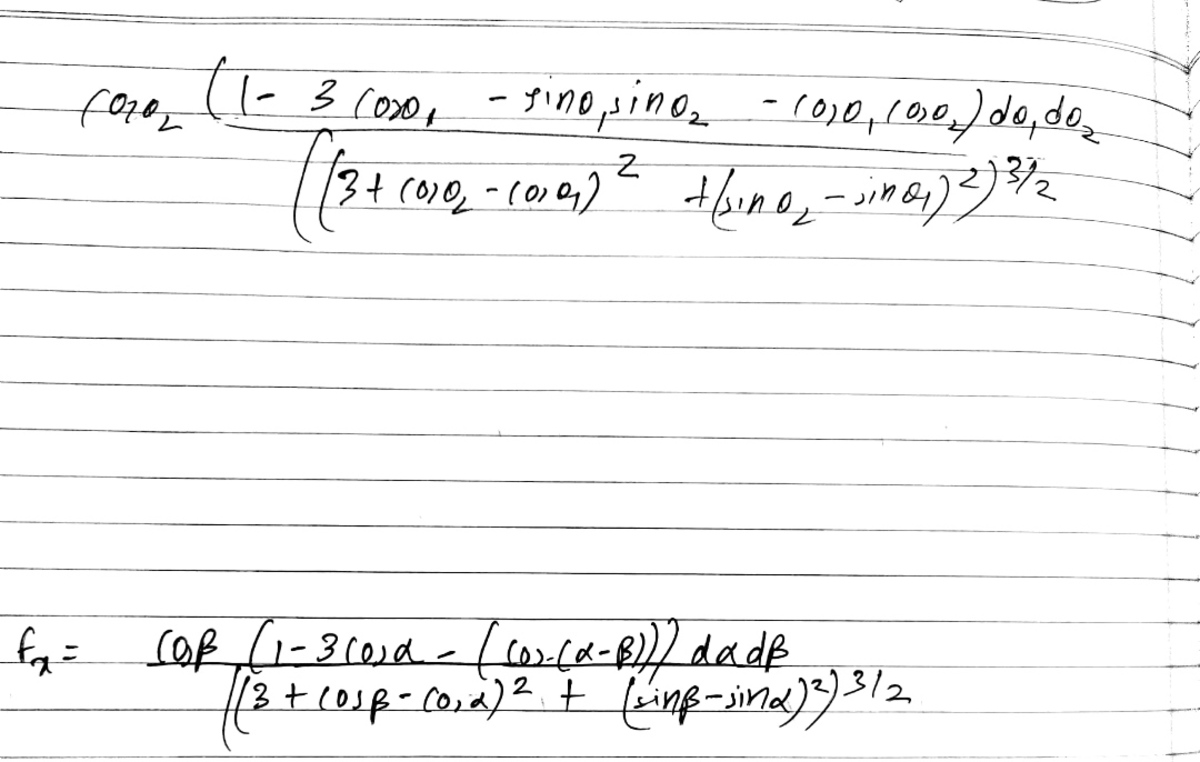
Log in to reply
@A Former Brilliant Member – I took the origin as the midpoint of the two circle centers. Thatis why we get different expressions. The expression that you get is okay. I made an error in my previous comment when I said 6.1. Ignore that. This integral that you got should evaluate to the right answer
Log in to reply
@Karan Chatrath – Wolfram is not evaluating. Sir can you tell me this integral answer.. In which college you are??
Log in to reply
Log in to reply
@Karan Chatrath – This snapshot is taken from wolfram. The answer is what I mentioned in the report.
Log in to reply
@Karan Chatrath – Oh yes finally I was making a mistake in typing wolfram. Now I am getting the right answer.
Log in to reply
@A Former Brilliant Member – Next time onwards, I request you to check your working very carefully before asking me to spot a mistake. It takes me time. Nevertheless, well done. Now you know the answer
Is this is the flux going through
−
z
in the new question of Steven chase. Flux through 2cm xy plane circle wil me equal to -z axis hemisphere,so here is the expression.u also getting the same expression and one more thing wolfram can't able to solve this.
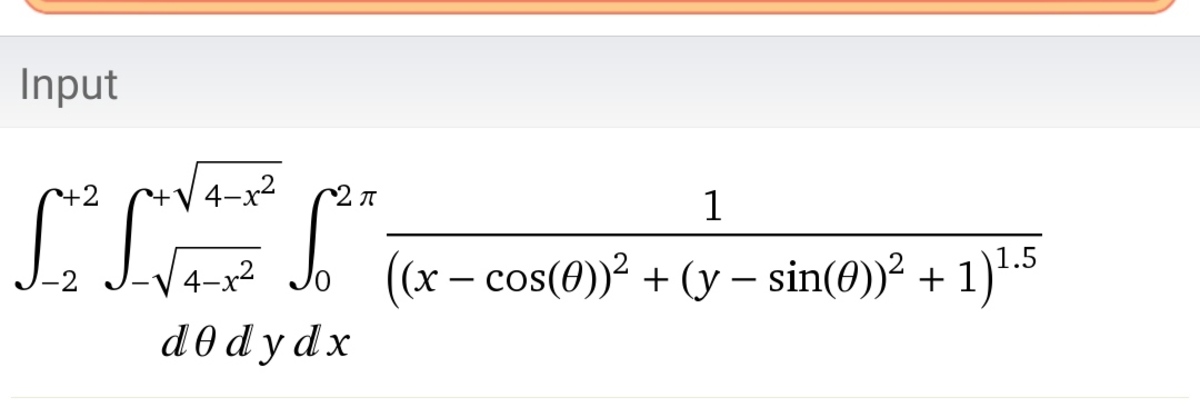
Log in to reply
@A Former Brilliant Member – This expression does not seem correct just by looking at it. I expect it to be much bigger. I used spherical coordinates and not cartesian coordinates to parameterise the sphere. And yes, the expression I get cannot be handled by Wolfram. I am calculating the results using a script of code.
Log in to reply
@Karan Chatrath – @Karan Chatrath ok fine. But i just want to discuss with you that the flux going through -z sphere will be equal to a circle kept on xy plane of radius 2 . So what is wrong with these assumption. From this assumtion question will be easier and I think after that there is no need of using spherical coordinates. Am I correct?
Log in to reply
@A Former Brilliant Member – You are correct. To calculate the flux through the negative hemisphere, your approach is a smart one. I had not thought of that. It makes the question much easier. Well done.
However, I would suggest that you use polar coordinates to parameterise the circle of radius 2.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
 Wolfram also failed in polar coordinates. I don't know how to write code. So what I do to solve the question?
Wolfram also failed in polar coordinates. I don't know how to write code. So what I do to solve the question?
Log in to reply
@A Former Brilliant Member – The integral evaluates to approximately 1.56. Now you should be able to get the answer to the question. Do post a solution. I got the answer in a more complicated way but your approach is smart
Log in to reply
@Karan Chatrath – I done integration with wolfram with a little smarter way , one little more assumtion is there. You can see the solution. And thank you for this integration I will post my 2nd solution using this integration.
Log in to reply
@A Former Brilliant Member – I saw it. Very impressive!
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
can you give me the answer of this integral
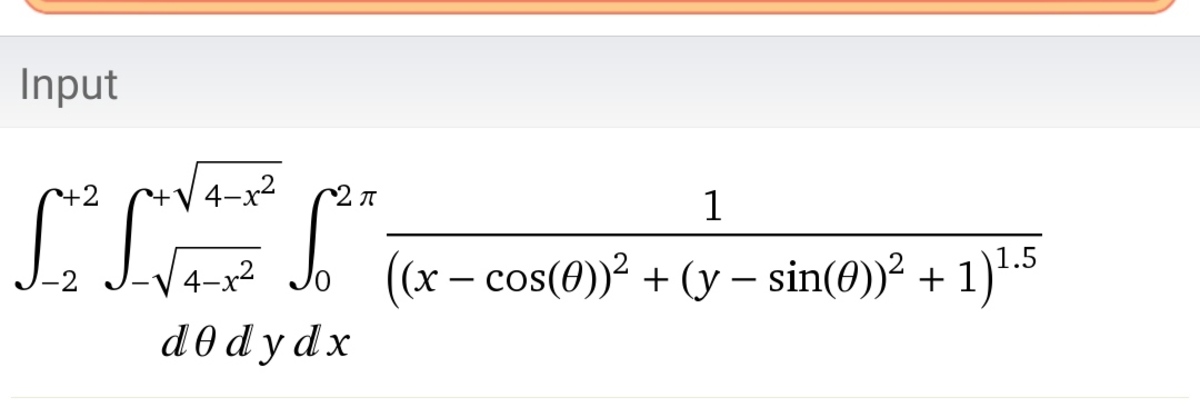
@Karan Chatrath
Sir can you help me in evaluating this integral
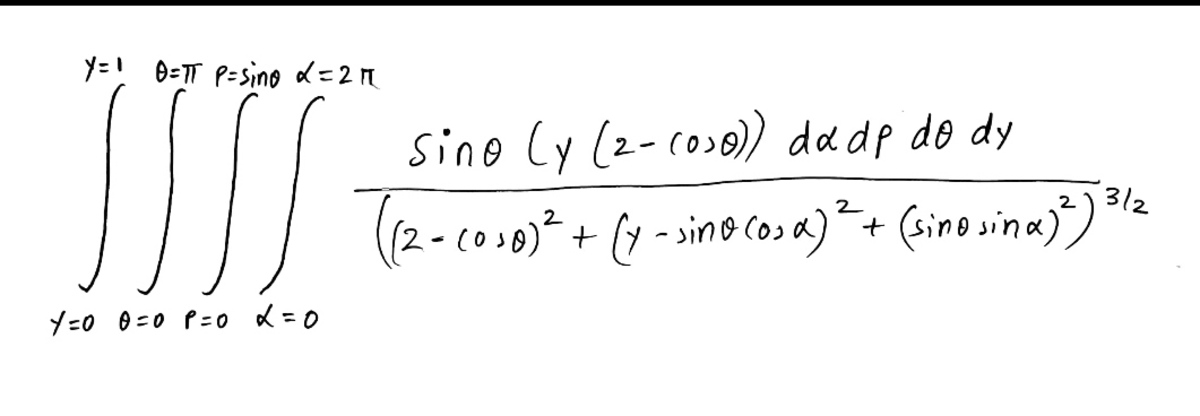
@Karan Chatrath Sir Can you please share your feelings with me as your Day streak has fallen from very high level ? N o t e - I just want to be motivate from you. Don't consider it as I am teasing you.
Log in to reply
@A Former Brilliant Member – Yes, it is disheartening. But it is just a streak.
Log in to reply
@Karan Chatrath – @Karan Chatrath Sir How do you get back your day streak??Did you know how to do time travel?? Please
Log in to reply
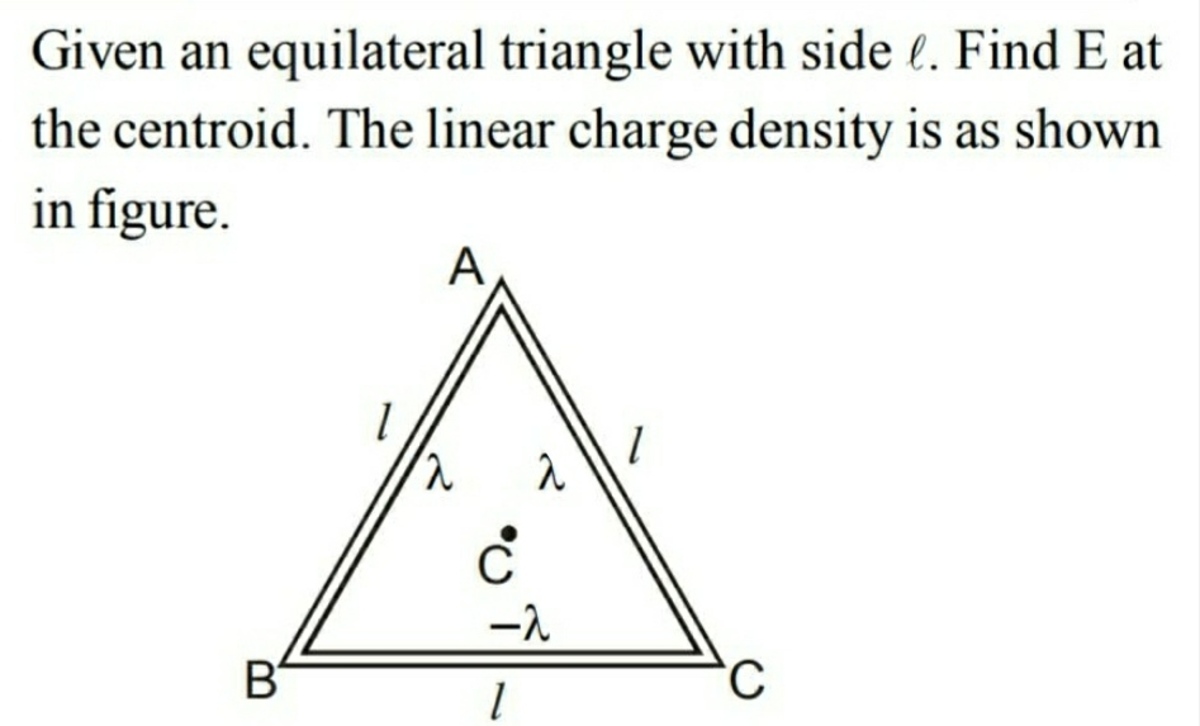
@A Former Brilliant Member
–
@Karan Chatrath Can you please tell me the answer of this question. I don't want solution. I was solving with book and my answer and book answer was not matching.
Log in to reply
@A Former Brilliant Member – Hi, I just saw your comment. I will try this problem after some time and share my answer.
Log in to reply
@Karan Chatrath – I get the net electric field to be downward with magnitude:
E = 2 π ϵ o L 9 λ
Log in to reply
@Karan Chatrath – @Karan Chatrath My answer is coming π ϵ 0 L 3 λ Answer according to book 2 π ϵ 0 L λ Answer according to my teacher 2 π ϵ 0 L 3 3 λ All these answers are in − j direction Can you recheck your answer one more time . In question two rods have linear charge density + λ and one rod have − λ
Log in to reply
@A Former Brilliant Member – Your answer is correct. I made an algebraic error. Now I get:
E = π ϵ o L 3 λ
@Karan Chatrath Sir can you please explain what does this expression mean ∇ × E = 0
Log in to reply
@A Former Brilliant Member – This denotes the curl of a vector field, which in this case is zero. You can google search this expression.
@Karan Chatrath
sir i was integrating
∫
0
1
x
2
d
x
from python from the tool a app (it's name is pydroid 3) . I downloaded it from google play store. But answer was not coming here is my work.

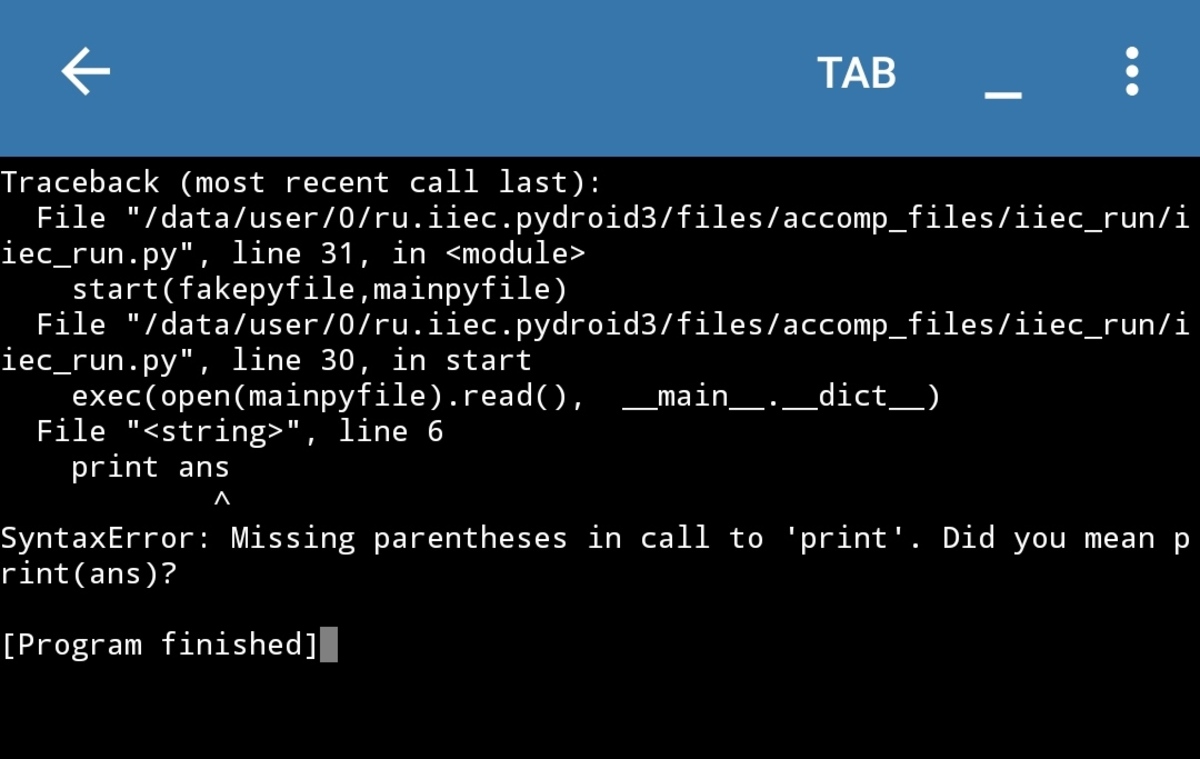
Log in to reply
@A Former Brilliant Member – Were there any other python files along with the one that you wrote?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 |
|
@Steven Chase
sir can I make animations through python. If yes how, suggest me a YouTube video?
Thanks in advance
My usual approach is to take a semi-analytical route, but a purely numerical approach is far more convenient. Attached here is the code I wrote. It is different, in terms of style and language, from that of @Steven Chase . See the lines which start with '%' sign as those lines explain each following step. Essentially, the code does the same as I would have done using a semi-analytical approach, but without tedious algebraic manipulations: