Sinusoidal Wire Magnetics (part 4 4 )

Electricity and Magnetism Level pending

A piece of wire has the following shape 0 ≤ x ≤ 2 π 0≤x≤2π y = sin ⁡ x y=\sin x z = 0 z=0 from position A A to B B . A circle of radius 1 1 is placed in Y − Z Y-Z plane. Both carries current of 2 π 2\sqrt{π} .What is the magnitude of magnetic force exerted between them.I have provided the view of system from + Y +Y axis.

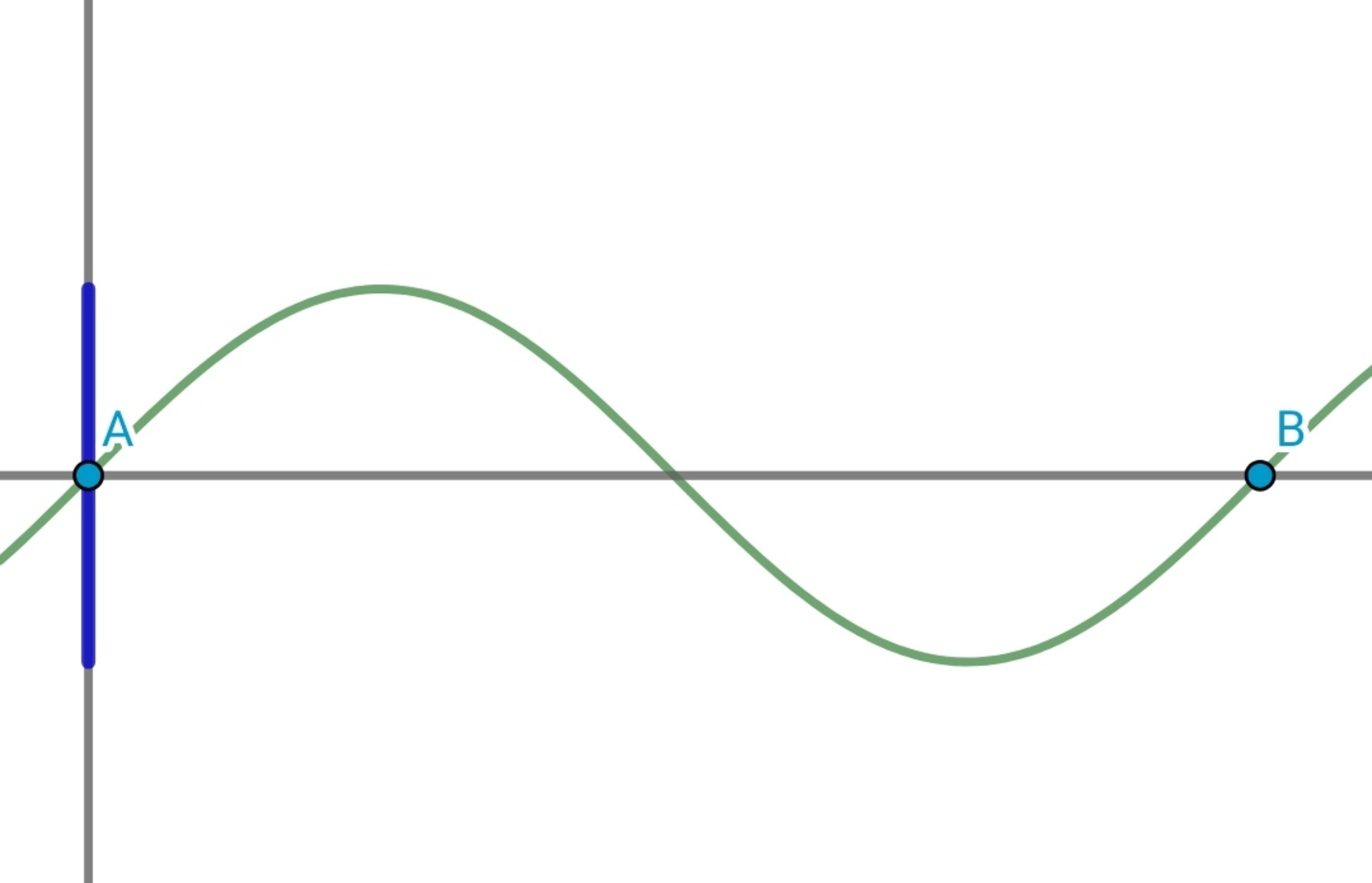
Details and Assumptions 1) Magnetic permeability μ 0 = 1 \mu_{0} =1


The answer is 1.826.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Steven Chase
Mar 19, 2020

Nice problem. Solution code attached: 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
 
import math

# Scan resolution

N = 10000

######################################################

# Constants

u0 = 1.0
I1 = 2.0*math.sqrt(math.pi)
I2 = 2.0*math.sqrt(math.pi)

dx1 = 2.0*math.pi/N
dtheta = 2.0*math.pi/N

######################################################
######################################################

# Wire 1 is the sinusoid
# Wire 2 is the circle

# For every point on wire 1, integrate over wire 2 to find the B field
# Then calculate the infinitesimal force contribution to wire 1
# Add up the infinitesimal force contributions

Fx = 0.0
Fy = 0.0
Fz = 0.0

x1 = 0.0

while x1 <= 2.0*math.pi:

    y1 = math.sin(x1)
    z1 = 0.0

    dy1 = math.cos(x1) * dx1
    dz1 = 0.0

    Bx = 0.0
    By = 0.0
    Bz = 0.0

    theta = 0.0
    x2 = 0.0

    while theta <= 2.0*math.pi:     # Determine B field at point on wire 1....
                                    # by integrating over wire 2
                                    # Biot Savart
        y2 = math.cos(theta)
        z2 = math.sin(theta)

        dx2 = 0.0
        dy2 = -math.sin(theta) * dtheta        
        dz2 = math.cos(theta) * dtheta

        rx = x1 - x2                 
        ry = y1 - y2
        rz = z1 - z2

        r = math.sqrt(rx**2.0 + ry**2.0 + rz**2.0)  

        Bcrossx = dy2*rz - dz2*ry      
        Bcrossy = -(dx2*rz - dz2*rx)
        Bcrossz = dx2*ry - dy2*rx

        dBx = (u0*I2/(4.0*math.pi))*Bcrossx/(r**3.0)  
        dBy = (u0*I2/(4.0*math.pi))*Bcrossy/(r**3.0)
        dBz = (u0*I2/(4.0*math.pi))*Bcrossz/(r**3.0)

        Bx = Bx + dBx
        By = By + dBy
        Bz = Bz + dBz

        theta = theta + dtheta

    Fcrossx = dy1*Bz - dz1*By        # Add up infinitesimal forces on wire 1
    Fcrossy = -(dx1*Bz - dz1*Bx)     # dF = I*(dL x B)
    Fcrossz = dx1*By - dy1*Bx

    dFx = I1 * Fcrossx
    dFy = I1 * Fcrossy
    dFz = I1 * Fcrossz

    Fx = Fx + dFx            
    Fy = Fy + dFy
    Fz = Fz + dFz

    x1 = x1 + dx1

######################################################
######################################################

# Print results

print N
print ""
print Fx
print Fy
print Fz
print ""
F = math.sqrt(Fx**2.0 + Fy**2.0 + Fz**2.0)

print F

######################################################
######################################################

#>>> 
#1000

#-1.77485676612e-14
#9.72537644059e-14
#-1.8408051273

#1.8408051273
#>>> ================================ RESTART ================================
#>>> 
#2000

#-1.82758909625e-14
#8.9307827061e-14
#-1.8335305663

#1.8335305663
#>>> ================================ RESTART ================================
#>>> 
#5000

#4.8616910172e-14
#-2.76391677998e-13
#-1.83019813904

#1.83019813904
#>>>


#10000

#6.04380868837e-14
#-3.45792702307e-13
#-1.82823188453

#1.82823188453

1 Helpful 1 Interesting 1 Brilliant 0 Confused

Amazing. Thanks for the solution. Can you please upload solution of infinite wire Magnetics??

A Former Brilliant Member - 1 year, 2 months ago

The infinite wire problem is similar to the sine magnetics Part 2 problem, just with a wider integration range. For the disk problem, we need more information about the current distribution.

Steven Chase - 1 year, 2 months ago

Log in to reply

@Steven Chase Current is distributed uniformly.

A Former Brilliant Member - 1 year, 2 months ago

Log in to reply

How does it flow? Does it circulate around the center?

Steven Chase - 1 year, 2 months ago

Log in to reply

@Steven Chase – Yes it circulate around the center . Sir i have taken a element at a distance x there multiply element's area with current per unit area in the whole disk.

A Former Brilliant Member - 1 year, 2 months ago

Log in to reply

@A Former Brilliant Member – I am not 100% sure that my answer of magnetic disc is correct. Can you check it by code??

A Former Brilliant Member - 1 year, 2 months ago

@Steven Chase Sir are you a Lead power engineer at Schweitzer Engineering Laboratories??

A Former Brilliant Member - 1 year, 2 months ago

Log in to reply

Yes, I am. You must have seen my profile on LinkedIn

Steven Chase - 1 year, 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...