Sinusoidal Wire Magnetics
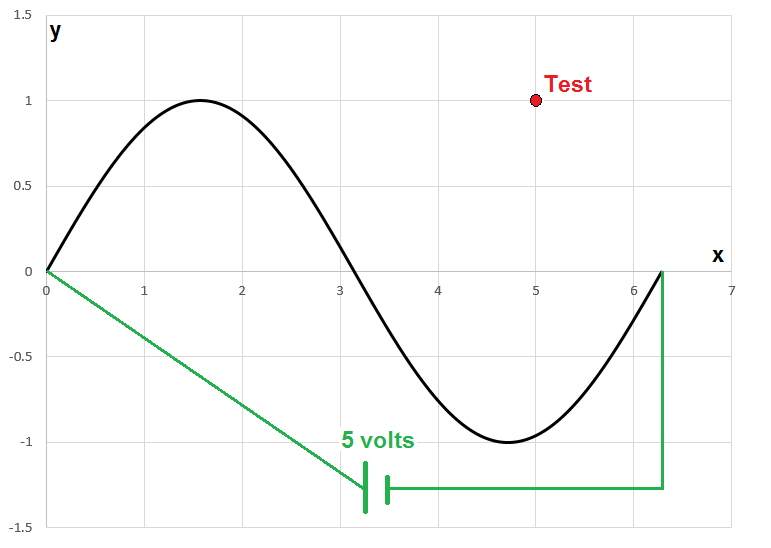
A piece of wire has the following shape:
0 ≤ x ≤ 2 π y = sin x z = 0
The wire has 1 unit of electrical resistance per unit length. A 5 volt DC battery is connected across the wire as shown.
What is the magnitude of the magnetic flux density ( B ) at test point ( x , y , z ) = ( 5 , 1 , 0 ) ?
Details and Assumptions:
1)
Neglect the field contributions from the battery wiring.
2)
Magnetic permeability
μ
0
=
1
, for simplicity
3)
The battery and battery wiring have no resistance
The answer is 0.0635.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Very nice solution, thanks. Out of curiosity, what integration method and step size did you use? I'm asking because my result was almost exactly 0.0635, running with explicit Euler and step sizes 1 0 − 4 , 1 0 − 5 , and 1 0 − 6 (very little variation between them).
Log in to reply
@Steven Chase Sir WOW!! This question is really awesome.Thanks for the question.From where do u get this type of questions?? Please post more questions like this. I am hungry!
Log in to reply
Thanks, glad you liked it. I just make the questions up myself. I can certainly post more in the future. Have you tried the most recent two?
Log in to reply
@Steven Chase – Yes.Trying to solve.
@Steven Chase – @Steven Chase sir can you frame a question like this one in which sin and cos both curve are involved and the question is to find B(magnetic field). I think it would be more interesting ?
Log in to reply
@A Former Brilliant Member – Can you be more specific about how to incorporate both sine and cosine?
Log in to reply
@Steven Chase – @Steven Chase sir Both sine and cosine curve are placed simultaneously in the x-y plane. And its obvious that cosine cure will be ahead π/2 by sine curve. Current is passing through both curve and we have to find resultant magnetic field at a specific point due to one cycle of both curve. Which will make question more interesting ?
@Steven Chase sir can you please upload the solution of this question https://brilliant.org/problems/very-involved-biot-savart-problem/
I used the RK-4 method with a step size of 1 0 − 5 . My result actually is 0.063499195705138 . I rounded it off to 0.0635.
Yeah, that's what I got too. But you wrote something else, so I was just curious
Log in to reply
@Steven Chase sir can you please upload the solution of your question {Very involved Biot savart problem}
@Steven Chase sir can you frame a question like this one in which sin and cos both curve are involved and the question is to find B(magnetic field). I think it would be more interesting ?
One can start by computing the resistance of the sinusoidal wire. This can be done by multiplying the resistance per unit length by the arc length of the sine wire. The expression for resistance is:
R = ∫ 0 2 π 1 + ( d x d y ) 2 d x Which is: R = ∫ 0 2 π 1 + cos 2 ( x ) d x
The current through the wire is computed using Ohm's law:
I = R 5
Now a general point P on the sinusoidal curve is parameterised as such:
r p = ( t , sin ( t ) , 0 )
The test point is: r t = ( 5 , 1 , 0 )
The vector joining the point P and the test point, directed away from P is:
r = r t − r p
The arc length vector is tangential to the curve:
d s = ( 1 , cos ( t ) , 0 )
Finally, the use of Biot-Savart law is made:
d B = 4 π μ o I ∣ r ∣ 3 d s × r
The vector is directed along the Z-axis only. This leads to:
∣ d B ∣ = 4 π I ( ( t − 5 ) 2 + ( sin ( t ) − 1 ) 2 ) 3 / 2 ( cos ( t ) ( t − 5 ) − sin ( t ) + 1 ) d t
∣ B ∣ = ∫ 0 2 π ⎝ ⎜ ⎛ 4 π I ( ( t − 5 ) 2 + ( sin ( t ) − 1 ) 2 ) 3 / 2 ( cos ( t ) ( t − 5 ) − sin ( t ) + 1 ) ⎠ ⎟ ⎞ d t
Integrating numerically gives the answer: ∣ B ∣ = 0 . 0 6 3 4 5
As always, it is a pleasure to solve your problems. Thank you for another good one.