Sky Region
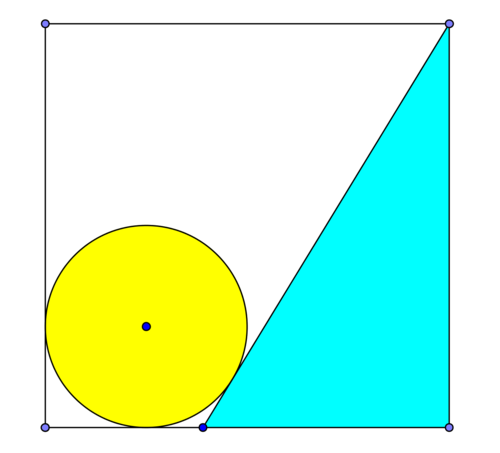 Find the area of the sky region if radius of circle is
4
1
and each side of the square is 1.
Find the area of the sky region if radius of circle is
4
1
and each side of the square is 1.
The area of sky region is looks like as c a − b , where a , b , c are positive integers and b is square free then find a + b − c .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Whelp, here's my 100% geometry solution since no one posted it yet.
Let A ( 0 , 0 ) , B ( 0 , 1 ) , C ( 1 , 1 ) , D ( 1 , 0 ) , P ( 4 1 , 4 1 ) , Q be the lower left vertex of the triangle, T be the point of tangency of the circle and the triangle, and R ( 4 1 , 0 ) (Hope you don't mind me using the same points as you :3)
Let R Q = x . Thus by tangents from a point being the same length, Q T = x . Now, remember that all tangents are perpendicular to the chord from the circle's center to the point of tangency.
So we have hypotenuse P C = 4 3 2 and the other leg P T = 4 1 .
Thus by Pythagorean theorem,
P C 2 − P T 2 = T C 2
⟶ T C = 4 1 7
Therefore, Q C = 4 1 7 + x
Looking at the blue triangle, we have Q D = 4 3 − x and Q C = 4 1 7 + x and C D = 1
Pythagorean theorem yields
Q C 2 = Q D 2 + C D 2
( 4 1 7 + x ) 2 = ( 4 3 − x ) 2 + 1
Algebra
x = 3 + 1 7 1
Thus the area of the triangle is one half the length of the base (since the height is 1) given by
2 1 ( 1 − r − x )
2 1 ( 1 − 4 1 − 3 + 1 7 1 ) = 1 6 9 − 1 7
Thus a + b − c = 9 + 1 7 − 1 6 = 1 0
Log in to reply
Didn't want to post my solution below as it would get buried. :3
Log in to reply
Nice solution and posting "strategy". This is a great question specifically because there are so many ways of solving it. The next obvious question is to find the radius of the largest circle that can be inscribed in the remaining portion of the square.
P.S.. "Algebra" .... haha. I tend to just use an arrow. :)
Log in to reply
@Brian Charlesworth – I had to ween myself off of the habit of using wolfram for linear equations with a radical of a constant. Those just became tedious and I didn't feel like doing them. Luckily I dont do that anymore. I stopped when on a contest I solved a 1 variable linear equation wrong after doing 5 minutes of math on the rest of the problem which is much harder than linear equations.
Log in to reply
@Trevor Arashiro – Yeah, it's the details where it's often easiest to trip up. I find I actually (for the most part) enjoy doing the small steps, (on paper, I just find it tedious to type them out in LaTeX), but then I didn't grow up with Wolfram, etc., or the internet, for that matter. That didn't make me feel like a dinosaur at all. :P
Really nice solution. One question though: How do you know the point P lies on the diagonal of the square AC? Can that be proved?
Log in to reply
Thanks. Yes, it can be proved. The diagonal A C lies along the line y = x , so since P ( 4 1 , 4 1 ) lies on this line it must also lie on the diagonal. A C .
perfect solution, sir!
I found the equation of the line through (1 1) which is tangent to the circle and then found where this line cut the X axis ....the area of the triangle follows
Write a comment or ask a question...
nice and well explained solution!! Thanks
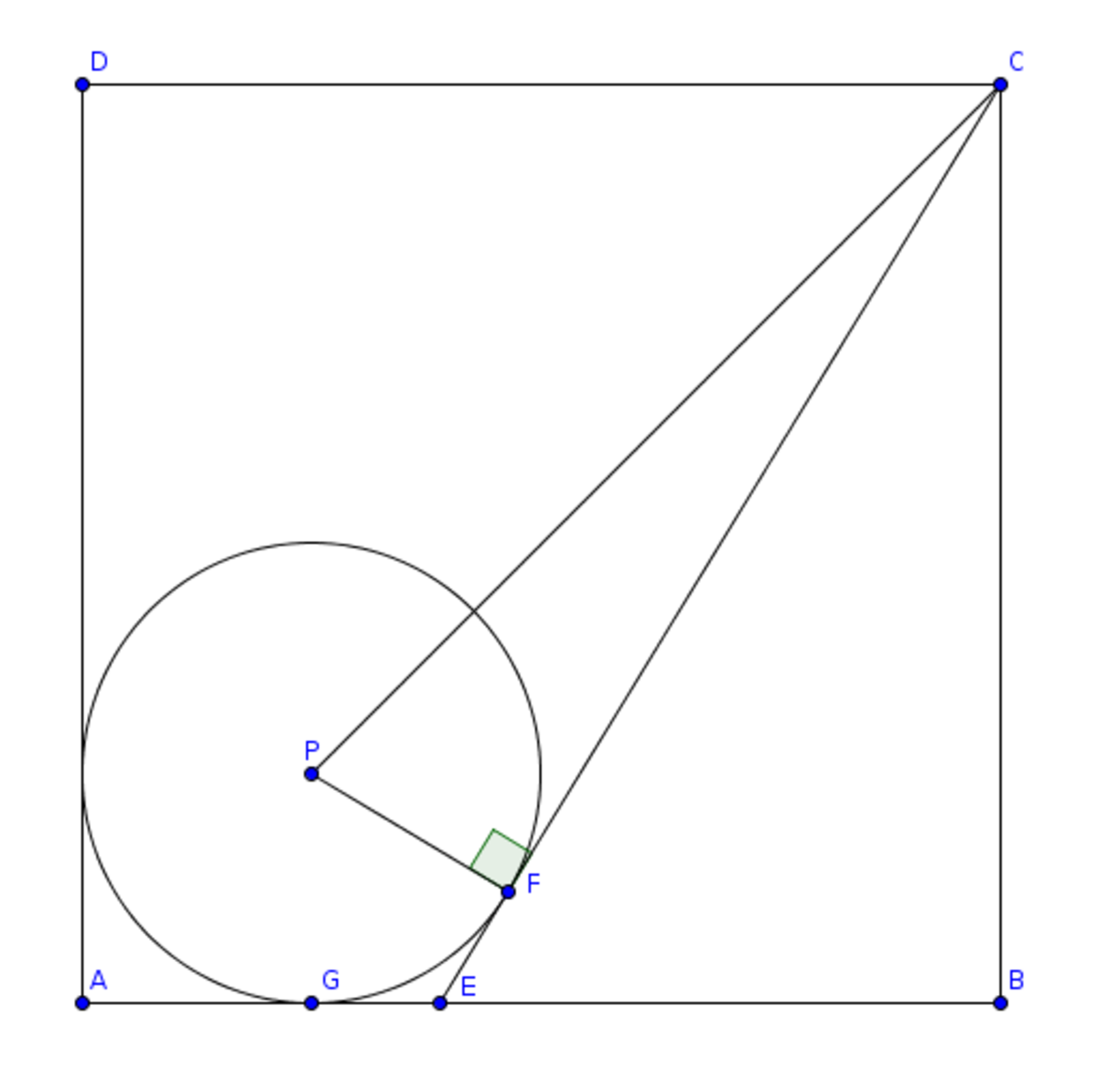 Let
A
,
B
,
C
,
D
be the corners of the square and
P
be the center of the circle.
E
is the lower left vertex of the triangle,
F
is the point of tangency of the circle and
C
E
,
G
is the point of tangency of the circle and
A
B
.
Let
A
,
B
,
C
,
D
be the corners of the square and
P
be the center of the circle.
E
is the lower left vertex of the triangle,
F
is the point of tangency of the circle and
C
E
,
G
is the point of tangency of the circle and
A
B
.
C E is tangent to the circle, so it's perpendicular to the radius P F .
∠ P F C = 9 0 ∘
The radius of the circle is 4 1 of the side of the square, so P C is ( 1 − 4 1 ) of the diagonal of the square.
P C = 4 3 × 2 = 4 3 2
P F = 4 1
In the right triangle P F C ,
C F 2 = P C 2 − P F 2
by the Pythagorean theorem.
So C F = P C 2 − P F 2 = 4 3 2 2 − 4 1 2 = 1 6 1 8 − 1 6 1 = 1 6 1 7 = 4 1 7
Both E F and G E are tangent to the circle and start from the same point E . So E F = G E
A G is equal to the radius of the circle, so A G = 4 1
A B = A G + G E + E B = 1
So G E + E B = A B − A G = 1 − 4 1 = 4 3
G E = 4 3 − E B
G E = F E = C E − C F = C E − 4 1 7
And then 4 3 − E B = C E − 4 1 7
C E = 4 3 + 1 7 − E B
In the right triangle C B E ,
E B 2 = C E 2 − B C 2 = C E 2 − 1
by the Pythagorean theorem.
E B 2 = ( 4 3 + 1 7 − E B ) 2 − 1 = 1 6 2 6 + 6 1 7 − 2 3 + 1 7 E B + E B 2 − 1
2 3 + 1 7 E B = 1 6 2 6 + 6 1 7 − 1 = 1 6 2 6 + 6 1 7 − 1 6 = 1 6 1 0 + 6 1 7 = 8 5 + 3 1 7
E B = 8 5 + 3 1 7 × 3 + 1 7 2 = 8 9 − 1 7
Now, the area of the triangle C B E is
A = 2 1 × E B × B C = 2 1 × E B = 2 1 × 8 9 − 1 7 = 1 6 9 − 1 7
The answer is 9 + 1 7 − 1 6 = 1 0
My approach was somewhat peasant way by using analytic geometry.
The sought area will be 1/2 (side)^2 times m, being m the slope of the vertex of sky region farthest from circle.
Procedure
1) First without loosing generality, we can assume side of square =4. and locate the circle tangent to it at the upper right corner so the resulting equations would be more handy, we are looking just for m
2) We take an straight line passing through the origin with an slope m.
3) Writing both equation and without solving completely we need just find the value of m that make the discriminant equal to 0 by doing so we get the values of m for the double roots that force precisely to be tangent,
Following the above we get for the for circle : (x-3)^2 + (y-3)^2 =1
for the straight line y =mx.
By substitution of y in circle equation we obtain (1+m^2)x^2 -6(1+m) +17 = 0
Forcing the discriminant equal to zero we get the equation after simplifying
4m^2- 9m +4 =0
which solution render the two possiblevalues of m tangents to the circle.
(9-17^.5)/8 and (9+17^.5)/8.
Therefore the sought area must be = (9-17^.5)/16
Thanks for a different approach.

Just for sake of variety .....
Let A ( 0 , 0 ) , B ( 0 , 1 ) , C ( 1 , 1 ) , D ( 1 , 0 ) be the corners of the square, P ( 4 1 , 4 1 ) be the center of the circle, Q be the lower left vertex of the triangle and T be the point of tangency of the circle and the triangle.
The area of the triangle will then be 2 1 tan ( ∠ Q C D ) , (since the side length of the square is 1 . )
Now ∠ Q C D = 2 π − ∠ B C P − ∠ P C T = 2 π − 4 π − sin − 1 ( P C ∣ ∣ P T ∣ ) =
4 π − sin − 1 ( 4 3 2 4 1 ) = 4 π − sin − 1 ( 6 2 ) .
So tan ( ∠ Q C D ) = 1 + tan ( sin − 1 ( 6 2 ) ) 1 − tan ( sin − 1 ( 6 2 ) ) =
1 + 1 7 1 7 1 − 1 7 1 7 = 1 7 + 1 1 7 − 1 = 8 9 − 1 7 .
The area of the triangle is then 1 6 9 − 1 7 , and so
a + b − c = 9 + 1 7 − 1 6 = 1 0 .