Slick Tensions

Classical Mechanics Level 2

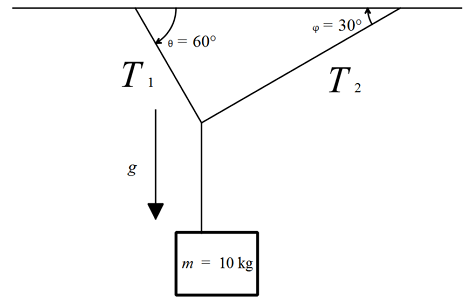
An object is hanging from a ceiling with the help of two cables arranged in such a way that a cable has a tension $T_1$ on the object and forms and angle $\theta=60^\circ$ with the ceiling and the other ones has a tension $T_2$ and makes an angle $\phi=30^\circ$ . If the object has a mass $m=10 \text{ kg}$ , calculate $|T_1| + |T_2|$ in Newtons to 2 decimal places.

In the image, $g$ is the acceleration due to gravity and has a value of $9.8 \text{ m/s}^2$ .

The answer is 133.87.

2 solutions

Erasmo Hinojosa
Apr 30, 2016

The slick solution arises from the fact that the cables are nicely arranged and form and angle of 90º degrees betweem them so that the force that balnces the wieght is equal to the vector sum of the tensions on the cables and all of these three forces form a nice righ triangle. If drawn correctly, it is easy to see that:

$T_1=mg \sin \theta$ and $T_2=mg \sin \phi$

Hence: $T_1 + T_2= 49(1 + \sqrt {3}) N = 133.87 N$

I used the same method! I solved a problem like this one in my book before.

Victor Paes Plinio - 5 years, 1 month ago

I think it would be better if you specified in your question the value of 'g' to be taken

Aayush Patni - 5 years, 1 month ago

Right, I changed it. Is it better now? Thanks for the feedback!

Erasmo Hinojosa - 5 years, 1 month ago

How did u derive the sin function

Amaya Solanki - 5 years, 1 month ago

Well, from the triangle that I mention in the answer above but that I do not show. You´ll have a force that balance the weight so it has the same magnitude as the weight but opposite direction and it should be the vectorial sum of the tensions since there are no other forces. So, by the nice geometry of the setup, the tensions would be the components of the force that balances the weight but along the direction of the tensions. So, you can draw a rigth triangle which is the geometrical reprsentation of a vectorial sum with the tensions as the sides and the sum of them as the hypothenus and the angles in this triangle would be $\theta$ and $\phi$ . Is it clearer now? If it is not, I invite you to use Newton´s Second Law for the components of forces in both x and y directions and to balance them, after some algebra and trigonometry, you should arrive to the same result.

Erasmo Hinojosa - 5 years, 1 month ago

Thanks Sir

Amaya Solanki - 5 years, 1 month ago

Oh, So you did it easily. I used a nuclear bomb to kill a mosquito, by using Lami's Theorem.Nice to meet a Physics Olympian :)

Swapnil Das - 5 years, 1 month ago

Yours is also a slick solution. Nice to meet you too.

Erasmo Hinojosa - 5 years, 1 month ago

You have become a inspiration for me, as you competed in the 47th IPhO. What sort of advice can you render to aspiring Physics Olympians, like me?

Swapnil Das - 5 years, 1 month ago

@Swapnil Das – Well, I haven´t competed yet but I have been chosen as part of the national team that will compete his year jeje. I recomend you reading a lot, some good books that I have used are, obviously, Univerty Physics by Sears-Zemansky, and Pysics for Scientists and Engineers by Serway and Jewett, some other more advanced books are Introduction to Classical Mechanics by David Morin (love this book, I started using the word "slick" because of this book), Introduction to Electrodynamics by D.J. Griffiths. Another advice is to looks for past olympics exams of as many nations as you can, every nation has unique problems, the best way to train to solve IPhO´s problems is not by trying past IPhO´s exams (because they are very difficult) but to try easier exams with similar style questions and similar syllabus. And train daily, because it takes a lot of time to cover so many topics and to become good at solving problems. I wish success and I belive you´ll get it if you keep solving problems.

Erasmo Hinojosa - 5 years, 1 month ago

@Erasmo Hinojosa – Thank you so very much!

Swapnil Das - 5 years, 1 month ago

I did this by resolving the components of tension in horizontal and vertical direction..

I.e

In horizontal direction, T1cosθ = T2cos(phi)

In vertical direction, T2sin(phi) + T1sinθ = mg

BUT from here, I am getting different values of T1 and T2..

WHY MY ASSUMPTION IS WRONG?

Ganesh Iyer - 5 years, 1 month ago

Your equations look right. Remember to use trigonometric identities to make the results look nice. Another way to write the magnitude of the tensions is: $T_1=mg cos \phi$ and $T_2=mg cos \theta$ It is probable that you get some factor of $sin \theta cos \phi + sin \phi cos \theta$ which reduces to 1 when substituting values.

Erasmo Hinojosa - 5 years, 1 month ago

Yes. Got it. Made silly mistake while doing calculation.

Ganesh Iyer - 5 years, 1 month ago

A Former Brilliant Member
Jun 8, 2016

Solution

Take the body of mass 10 as the system.The forces acting on the system are
(i) $10g$ downwards (by the earth),
(ii) $T_1$ along the first sting,
(iii) $T_2$ along the second string.

As the body is in equilibrium, these forces must add to zero.Taking horizontal components,

$\Rightarrow T_2 \cos 30°=T_1 \cos 60°$

$T_1=\sqrt{3}T_2$ .... $(1)$

Taking vertical components,

$N=T_1 \sin 60°+T_2 \sin 30°$

$\Rightarrow 10g=N$

$10×9.8=T_1 \sin 60°+T_2 \sin 30°$

$98=T_1 ×\dfrac{\sqrt{3}}{2}+T_2 ×\dfrac{1}{2}$

Using $(1)$ .

$98=T_2×\dfrac{3}{2}+T_2×\dfrac{1}{2}$

$T_2=49$

And, $T_1=49\sqrt{3}$ .

$\therefore T_1+T_2=49(1+\sqrt{3})\approx \boxed{133.87}$

Slick Tensions

The answer is 133.87.

2 solutions

0 pending reports