Slid sectors

Due to symmetry, the two equilateral triangles share a common centroid $O$ . The side length of the big equilateral triangle is given by $2\sqrt 3OP$ , where $OP$ is the perpendicular distance between the centroid and the base. An $OP$ is given by:

$\begin{aligned} OP & = QS-QR & \small \color{#3D99F6} \text{Let }\angle SQT = \theta \\ & = QS - OQ\cos (\theta + 30^\circ) & \small \color{#3D99F6} \text{Note that }QS = 20, \ OQ = 9 \times \frac {\sqrt 3}2 \times \frac 23 = 3\sqrt 3 \\ & = 20 - 3\sqrt 3 \left(\frac {\sqrt 3}2\cos \theta - \frac 12 \sin \theta\right) & \small \color{#3D99F6} \text{and }\cos \theta = \frac {QS}{QT} = \frac {20}{20+9} = \frac {20}{29}, \ \sin \theta = \frac {21}{29} \\ & = 20 - 3\sqrt 3 \left(\frac {\sqrt 3}2 \times \frac {20}{29} - \frac 12 \times \frac {21}{29} \right) \end{aligned}$

Therefore, the side length of the big equilateral triangle is:

$\begin{aligned} 2\sqrt 3 OP & = 2\sqrt 3 \left(20 - 3\sqrt 3 \left(\frac {\sqrt 3}2 \times \frac {20}{29} - \frac 12 \times \frac {21}{29} \right) \right) \\ & = 40\sqrt 3 - \frac {180\sqrt 3 - 189}{29} \\ & = \frac {189+980\sqrt 3}{29} \end{aligned}$

Hence, $a+b+c+d = 189+980 + 29 + 3 = \boxed{1201}$ .

Let the points be labelled as shown, and draw $BD$ so that $BD \perp AH$ at $B$ , and draw $BC$ . Let $\theta = \angle BDG$ , let $a = BC$ , let $b = AC$ , and let $c = AB$ . By symmetry, $GH = AC = b$ .

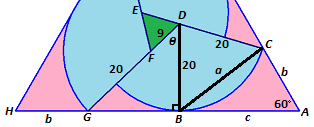
Since $DG = 29$ and $BD = 20$ , then by Pythagorean's Theorem on $\triangle BDG$ , $BG = \sqrt{29^2 - 20^2} = 21$ , and $\sin \theta = \frac{21}{29}$ and $\cos \theta = \frac{20}{29}$ .

Since $\angle CDE = 180°$ and $\angle EDF = 60°$ , $\angle EDF = 120° - \theta$ . Since $\triangle BCD$ is an isosceles triangle, $\angle DBC = \frac{180° - (120° - \theta)}{2} = 30° + \frac{\theta}{2}$ . Since $\angle ABD$ is a right angle, $\angle ABC = 90° - (30° + \frac{\theta}{2}) = 60° - \frac{\theta}{2}$ . Finally, since $\angle ABC = 60° - \frac{\theta}{2}$ and $\angle BAC = 60°$ , by triangle sum in $\triangle ABC$ $\angle ACB = 180° - 60° - (60° - \frac{\theta}{2}) = 60° + \frac{\theta}{2}$ .

By the law of sines on $\triangle ABC$ , $b = \frac{a}{\sin 60°}\sin (60° - \frac{\theta}{2})$ and $c = \frac{a}{\sin 60°}\sin (60° + \frac{\theta}{2})$ . The side length $AH$ is $AH = AB + BG + GH = c + 21 + b$ which simplifies to $AH = 21 + 2a \cos \frac{\theta}{2}$ .

Now $a$ is a chord with central angle $120° - \theta$ of a circle with radius $20$ , so $a = 2 \cdot 20 \sin \frac{1}{2}(120° - \theta) = 20 \sqrt{3} \cos \frac{\theta}{2} - 20 \sin \frac{\theta}{2}$ .

Substituting this value into $AH$ and simplifying gives $AH = 21 + 20\sqrt{3} + 20\sqrt{3} \cos \theta - 20 \sin \theta$ , and substituting $\sin \theta = \frac{21}{29}$ and $\cos \theta = \frac{20}{29}$ from above and simplifying gives $\frac{189 + 980\sqrt{3}}{29}$ , which means $a = 189$ , $b = 980$ , $c = 29$ , and $d = 3$ ; and $a + b + c + d = 189 + 980 + 29 + 3 = \boxed{1201}$ .

While, the geometric solution using (20,21,29) right triangle, the side of large equilateral triangle is given by:

a = (189+980√3)/29,

However, the algebraic answer derived using the area relation:

(a^2-9^2)((√3)/4)=3(Area Quadrialteral)

Area Quadrilateral= Area of two triangles=(20×29+(a-b)×b)((√3)/4), where, b is the length between triangle and circle vertice on the side of the triangle.

gives an equation:

a^2 - 9^2=3×20×29 + 3(a-b)b

Solving this as Diophantine equation gives 'a' and 'b' as,

a=69 and b =20.

This algebraic integer value of a=69 is quite different from the geometric value of a=~65.048.

$a$ and $b$ are not coprimes, they share the common factor $7$