Sliding bead
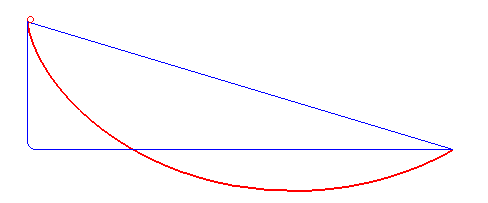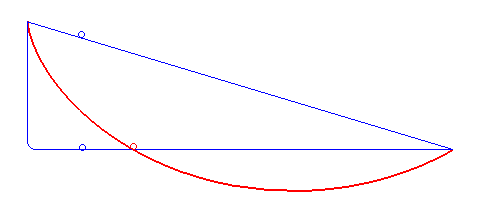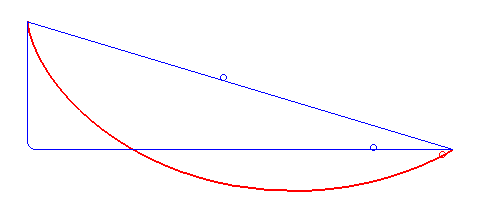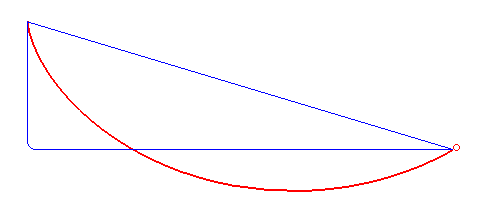 A bead is released from a certain point and slides down a frictionless wire that
connects this point to another point, as shown in the figure above. What shape should the wire take so
that the bead reaches the endpoint in the shortest possible time?
A bead is released from a certain point and slides down a frictionless wire that
connects this point to another point, as shown in the figure above. What shape should the wire take so
that the bead reaches the endpoint in the shortest possible time?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice gif! Did you make it yourself? If so, how did you do it?
In all paths energy stored in bed will be same but when on releasing bed it will took same time via all paths... Am i right ??? :[
Thanks
ok
Why not a Hyperbolic Spiral?
Log in to reply
Any reason why it should be a hyperbolic spiral?
Log in to reply
Actually I was imagining it, how the speed would go and how less time it will take. The spiral seemed like a good enough answer.
Log in to reply
@Maham Zaidi – It can't be a hyperbolic spiral as taking the origin as the two perpendicular lines , this becomes a rectangular hyperbola, which only tends to 0 , but here it is clearly becoming 0 for two values
@Maham Zaidi – The math don't lie.
I dont think it will be a cycloid ghis time as the brachistochrone is a cycloid when initial and final points are at the same level.......
I'm not sure why this is level 3, but I like the gif. I also like cycloids, so I like this question.
it should be level 2 or level 4/5 ? ccording to you ...??
Calculus of Variations: extremize the integral : sqrt(1+(dy/dx)2)/sqrt(19.6 y). This will give you the minimum time. the numerator is the distance in infinitesimal calculus and denominator is the velocity as the particle moves along the trajectory. velocity sqrt(19.6 y) can be obtained by conservation of energy. Now solve this using Lagrange's equation popular in classical mechanics or calculus of variations.
It is similar to the brachistochrone problem, just that in the brachistochrone problem the wires are in the shape of an inverted cycloid (a tautochrone), an incline and a cycloid.
This is called the brachistochrone .