Sliding Coins
A coin is placed on top of a hemisphere of radius
1
m
. The coin begins to slide from rest down the side of the hemisphere without friction. At what height
in meters
will the coin stop being in contact with the surface of the hemisphere?
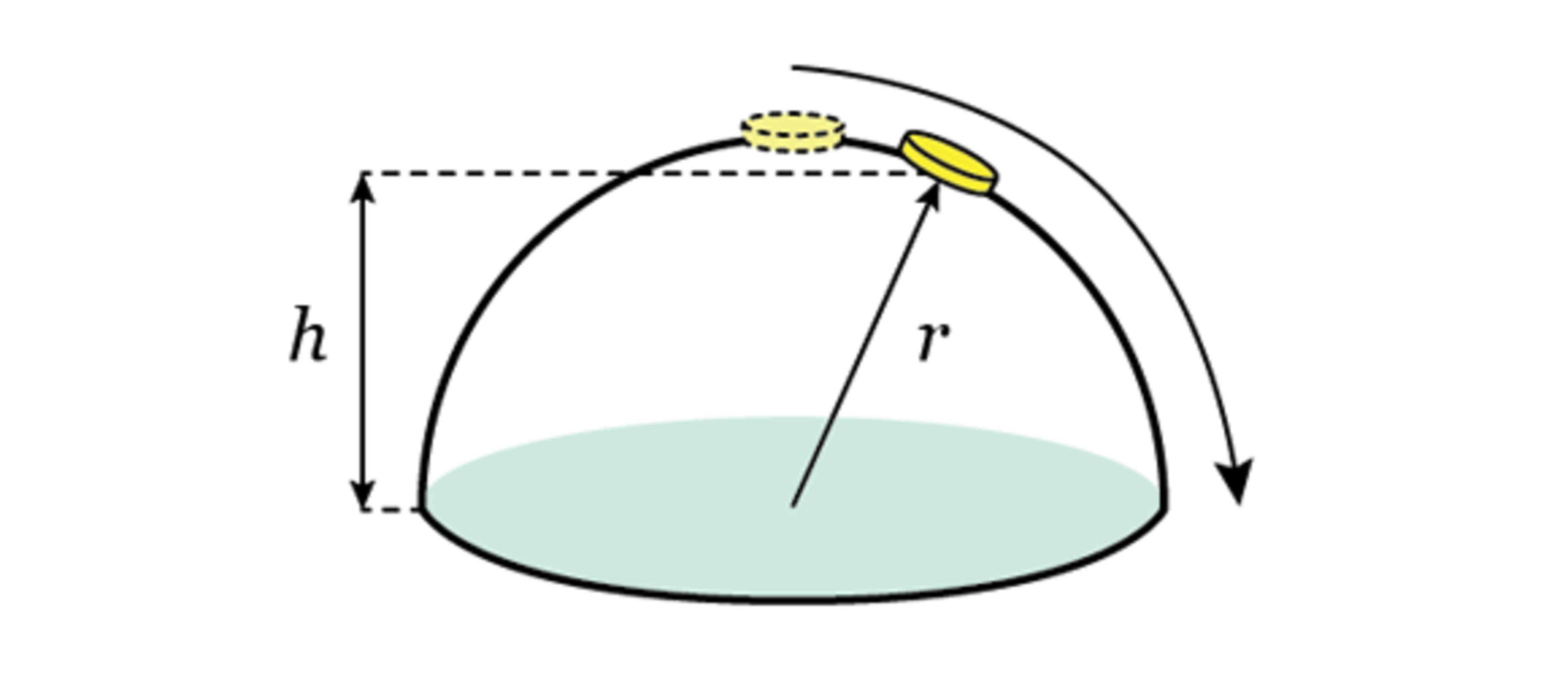
The answer is 0.667.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
A coin is placed on top of a hemisphere of radius 1 m. The coin begins to slide from rest down the side of the hemisphere without friction. At what height in meters will the coin stop being in contact with the surface of the hemisphere? As there is no friction, mechanical energy is conserved. As elastic potential energy is held constant in this problem, only the kinetic energy of the coin and its gravitational potential energy are changing. Assume that gravitational potential energy is zero at the top of the hemisphere. Then if v is the velocity at a time where the coin is h meters above the ground and m is the mass of the coin, then (1/2)mv^2-mg(1-h)=0 ==> v=sqrt(2g(1-h)). Whenever the coin is in contact with the hemisphere, the velocity is directly perpendicular to the radial vector towards the coin.The angle that the radial vector makes with respect to the diameter of the hemisphere is arcsin(h) above the axis, so the angle that the velocity vector makes with respect to the diameter of the hemisphere is arccos(h) below the axis. Since the velocity is given by sqrt(2g(1-h)), we have that the horizontal velocity is v x=h*sqrt(2g(1-h)) away from the hemisphere (to the right) and the vertical velocity is v y=-sqrt(2g(1-h^2)(1-h)) (downward). The coin leaves the surface of the hemisphere when the downward acceleration would exceed g otherwise. Thus we need to find the rate of change of the vertical velocity with respect to time. Here we use the chain rule several times. -sqrt(2g(1-h^2)(1-h)) is a function of h, so we differentiate with respect to h: dv y/dh=-(1/[2*sqrt(2g(1-h^2)(1-h)]) * [-2g(1-h^2)-4gh(1-h)] However, this is the rate of change of vertical velocity with respect to h. We therefore must use the chain rule again to differentiate with respect to time. This is easily done: dv y/dt=-(1/[2*sqrt(2g(1-h^2)(1-h)]) * [-2g(1-h^2)-4gh(1-h)] *dh/dt. However, dh/dt=v=-sqrt(2g(1-h^2)(1-h)). We can cancel this out: dv y/dt=-g(1-h^2)-2gh(1-h)=-g(1+2h-3h^2). We're solving for when dv y/dt=-g; in other words 1+2h-3h^2=1. Solving for h gives h=2/3.
consider initial point as A and point at which coin slips is B
Solution: we will apply law of conservation of energy ie KE+PE(At A)=KE+PE(At B)..........................1
KE initial =0 PE initial=0(as i considered the point A as reference axis)
AT B, KE final=1/2 mv2 PE final=-mg(r-h) {h is given}
and, h/r =cosθ hence applying eqn. 1
we get, 1/2mv2=mgr(1-cosθ)...................2
for velocity, AT THE POINT OF SLIPPING THE NORMAL REACTION EXERTED BETWEEN THE SPHERE AND COIN IS 0 :::N+MGCOSθ=MV2/R(for centripetal) N=O hence,mv2=mgrcosθ...............4
putting values in 2 from 4, (mgrcosθ)/2=mgr(1-cosθ)
hence, cosθ=2/3
h=0.66r
Ans=0.66
By work-energy theorem:- 1/2m(v^2-u^2)=mgr(1-cos thita) So. v^2=2gr(1-cos thita)
When coin will leave the surface normal will be ZERO So. mg cos thita=mv^2/r Putting the value of V^2 we will get 2g(1-cos thita)=g cos thita So we will get Cos thita =2/3
So height descended will be r(1-cos thita)=1/3 Therefor height from surface from hemisphere will be 1-1/3=2/3=0.66
Thanx take it easy
Suppose the coin loses contact with the hemisphere at the point where height is given by h 0 , and the angle it makes with the horizontal surface is θ
Hence we have h 0 = r s i n θ
By conservation of energy,
m g h = 2 1 m v 2 + m g h 0 ,
where v denotes the tangential velocity at the point when the coin loses contact with the surface.
Rearranging, we have
m g ( 1 − s i n θ ) = 2 1 m v 2
v 2 = 2 g ( 1 − s i n θ )
At the instant when the coin stops being in contact with the surface, the normal force exerted by the hemisphere equals 0 .
Therefore the only forces acting on the coin at that particular instant are its weight and the centripetal force.
We can then write the equation,
m g s i n θ = r m v 2
g r s i n θ = v 2
subbing in the expression we previously obtained for v 2
g r s i n θ = 2 g ( 1 − s i n θ )
since r = 1 , we get
3 s i n θ = 2
h 0 = s i n θ = 3 2
The answer is 0 . 6 6 7
Dude, your explanation is majestic
0 0!
Let at an angle θ with respect to vertical , the coin loses its contact .Let this point be its final position.
Applying conservation of energy at initial and final points. We get
m g r = m g r cos θ + 2 m v 2
Also at the point of contact , m g cos θ = r m v 2
Plugging the value of m v 2 in first equation, we obtain
m g r = m g r cos θ + 2 m g r cos θ
This implies cos θ = 2 / 3
Hence , h = r cos θ = 0 . 6 6 6 6 7
Let B be the angle between the vertical through the centre and top of the hemisphere and a radius from the centre to the coin's position at some time t. The height lost by the coin at this point is 1– cos B.
The potential energy lost = kinetic energy gained by the coin, that is
m g (1–cos B) = (1/2) m v^2 (1)
where v is the coin's speed at that point.
At this point, the component of the coin's weight normal to the hemisphere surface is m g cos B. The centripetal fore required to keep it moving in a circle of radius r with speed v is m*v^2/r. (Here r=1 m.) When these 2 forces are equal we have:
m g cos B = m*v^2 (2)
From (1) and (2), we can get m g cos B = 2(1–cos B) m g.
Cancelling out m and g, we get cos B = 2 – 2cos B. So, cos B = 2/3 , thus h = cos B = 2/3 which is approximately 0.667 m.
Since the total energy is constant, we have: 2 m v 2 = m g r ( 1 − cos α ) or v 2 = 2 g r ( 1 − cos α ) where α is the angle of the radius vector associating with the coin and the vertical axis.
The coin stops being in contact with the hemisphere when interactive force between them N = 0 or m g cos α = r m v 2 .
Therefore, g r cos α = v 2 = 2 g r ( 1 − cos α ) or cos α = 3 2 .
The answer is: h = r cos α = 3 2 r = 0 . 6 6 7 ( m )
The coin slips off when the normal force is equal to zero.
F N = m g c o s θ − m a c = 0
g c o s θ = a c = r v 2
By conservation of energy (because there is no friction),
Δ E t o t a l = Δ E K i n e t i c + Δ E P o t e n t i a l = 0 .
So:
Δ E K i n e t i c = − Δ E P o t e n t i a l
2 1 m v 2 = − m g ( h − r )
v 2 = 2 g ( r − h )
So, substituting into the previous expression:
g c o s θ = r 2 g ( r − h )
Now, we know that c o s θ = r h from the problem's geometry.
Thus,
r g h = r 2 g ( r − h )
h = 2 ( r − h )
3 h = 2 r
h = 2 r / 3
h = 3 2 m ≈ 0 . 6 6 7 m
how come Fn=mgcos-mac and not mgcos + mac, it'll be great if you could explain thanks
Log in to reply
In this case, a c is the centripetal acceleration, so since m a c = m g c o s θ − F n (as you can see from a free-body diagram), F n = m g c o s θ − m a c .
Log in to reply
but couldn't you also set it going positive in the going up direction which would make it, mac=Fn-mgcos ?
Log in to reply
@Jian Feng Gao – Oh, I see what you mean! In this answer, I didn't make g negative. Instead, I accounted for the different directions of the forces by subtracting rather than adding, for example. We both centripetal acceleration is outward, the normal force is outward, and the force of gravity is inward. Your g = − 9 . 8 m / s 2 , while my g = 9 . 8 m / s 2 . That's the only difference.
Log in to reply
@Enric Boix – how come centripetal acceleration is outward? I thought it always went inward when going in a circular path.
Let , at the time of leaving, its velocity is v Normal reaction =0 ⇒ r m v 2 = m g c o s θ where θ is the angle which it makes with vertical. Also , by conservation of energy, m g ( r − h ) = 2 m v 2 Solving these two equations, taking cos θ = r h we get: h = 3 2 = 0 . 6 6 7
Let the angle made by the coin with respect to the centre of the base be θ .
So, c o s θ = h / r
or equivalently
(i) r c o s θ = h .
For the coin as it slides m g c o s θ − N = m v 2 / r
(where N is normal force).
When it loses its contact with sphere N = 0 , and so
m g c o s θ = m v 2 / r
and
(ii) r g c o s θ = v 2 .
By conservation of energy v = 2 g ( r − h ) .
We then have from (ii)
2 g ( r − h ) = r g c o s θ
and so
2 ( r − h ) = r c o s θ .
Incorporating (i) we have
2 r − 2 r c o s θ = r c o s θ
which can be solved for
c o s θ = 2 / 3 .
Therefore h = r c o s θ = 2 r / 3 = 2 / 3 .