Sliding Squares
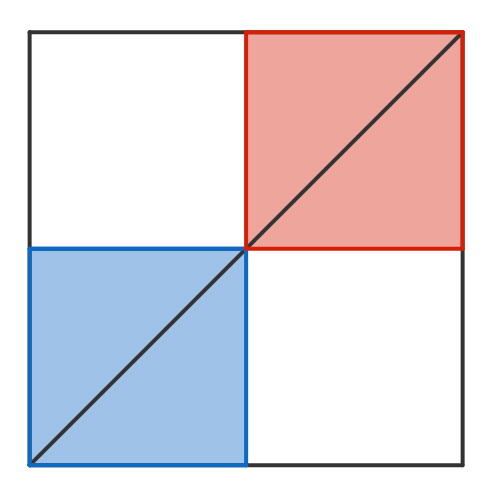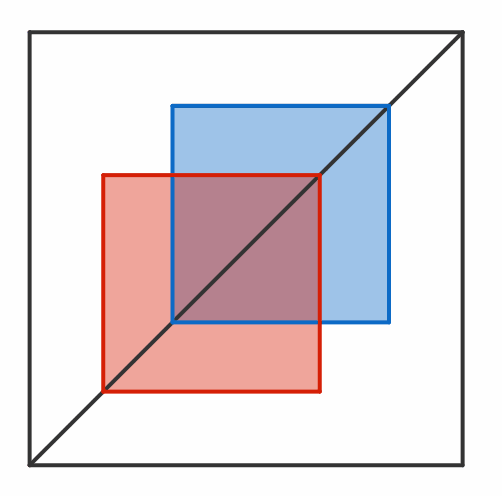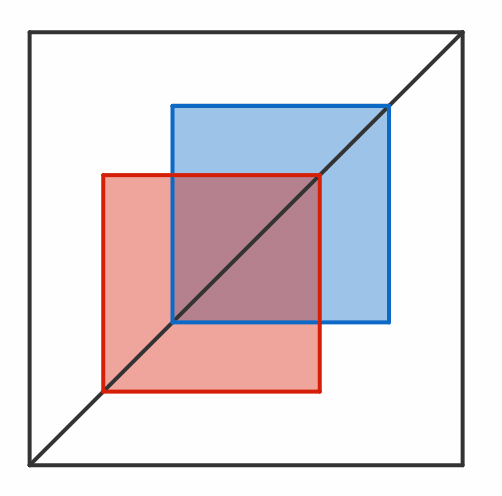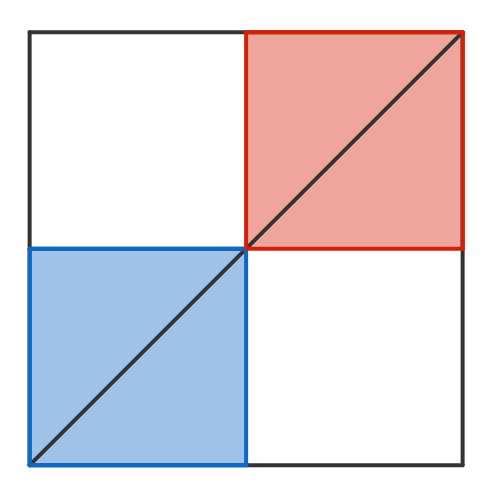
There are 2 squares of side length 1 that begin in opposite corners of a larger 2 × 2 square. Both squares slide diagonally towards each other (at the same speed) until they are in the corners opposite to those they started in. This process is then repeated in the opposite direction.
What is the average area of overlap between the two squares?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Does the fact that dy=dx get us to the x^2 term? Also, why is the integral from 0 to 1. Thanks! :)
Log in to reply
Yes. The overlapping area equals Δ x ⋅ Δ y and since Δ x = Δ y we've got the x 2 term. Since 0 ≤ Δ x ≤ 1 , we integrate from 0 to 1. Hope that answers your question.
I think it's because we are talking about the area of the square, and if y=x, then the area of the square is y*x or x^2. Its the way I thought about it. The overlapping area is changing only inside the red square, which has a base of 1, thus it's only moving between 0 and 1, and it gives us the integration limits.
Why x^2 dx?
Log in to reply
The overlapping area equals Δ x ⋅ Δ y and since Δ x = Δ y we've got the x 2 term. Maybe it would've been clearer if I had used Δ x 2 , but that's just a sign denoting variable so it's not that important.
why this integral and why the bounds of 0 and 1 on the integral?
Isn't x^2dx a volume element as X has the dimensions of length. And here how is the average area of overlap defined? Isn't it ∫Adt/∫dt where A is tye area overlaped
Log in to reply
You can get from your expression to mine by applying chain rule: d t = v 1 d x .
Let x be the distance between the left side of the left unit square (and by symmetry, the right side of the right unit square) and let s be the length of the overlapped square formed in the center.
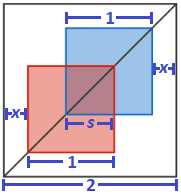
Then comparing horizontal segments, we have 2 = 2 x + ( 1 − s ) + s + ( 1 − s ) , which simplifies to s = 2 x , for an overlapping area of A = 4 x 2 for 0 ≤ x ≤ 2 1 . Since the process is symmetrical, we only need to consider this interval.
The average area is then 2 1 − 0 ∫ 0 2 1 4 x 2 d x = 3 1 .
Can't this be done without integration??
Log in to reply
I suppose you could use that the area under the parabola is 1/3 of the area of the rectangle it encloses instead of integrating.
Log in to reply
How do we prove this??
Log in to reply
@Mr. India – The parabola y = 4 x 2 goes through ( 0 , 0 ) and ( 2 1 , 1 ) . The area under the curve for this interval [ 0 , 2 1 ] is 3 1 ( 2 1 ⋅ 1 ) = 6 1 . The average height in this interval [ 0 , 2 1 ] is therefore 2 1 6 1 = 3 1 .
why are the bounds for x between 0 and 1/2?
Log in to reply
The smallest x can be is 0 (when the red and blue squares are in the corners of the big square) and the biggest x can be is 1/2 (when the red and blue squares completely overlap), so x is between 0 and 1/2.
Let's introduce a time variable t and a(t)=the area at time t. Set t=0 when the red is at its lowest position and t=4 when the animation has completed a cycle. a(0)=0, a(1)=1. The second second t=1 to t=2 is just the reverse of the first second as the red reaches the upper corner and the final two seconds are the same as the first two. Each of the four seconds is symmetrical in terms of overlap, so we can just consider the overlap from t=0 to t=1.
The overlap area a ( t ) = t 2 . Integrating this from 0 to 1 gives the solution 3 1
Let x be the lenght of the overlapped square's side. Area changes with a function g ( x ) such that:
g ( x ) = { x 2 i f 0 ≤ x < 1 ( x − 2 ) 2 i f 1 ≤ x ≤ 2 }
It's clear that ∫ 0 2 g ( x ) d x = ∫ 0 2 ( x − 1 ) 2 d x :
Now, what the problem is asking is to find f ( c ) where f ( x ) = ( x − 1 ) 2 such that ∫ 0 2 f ( x ) d x = ( 2 − 0 ) f ( c ) = 2 f ( c ) . (If you don't understand this, you may check Mean Value Theorem for Integrals , which states that if f ( x ) is a continuous function on [ a , b ] there exists c ∈ [ a , b ] such that b − a 1 ∫ a b f ( x ) d x = f ( c ) ). Therefore,
f ( c ) = 2 1 ∫ 0 2 ( x − 1 ) 2 d x = 2 1 ⋅ 3 2 = 3 1
Is it overly simplistic to see it like this: at the beginning of each movement the overlap is 0%, at the middle 100% and at the end 0%. The overlap varies smoothly between these three, which are equally spaced, so the average overlap is the average of 0%, 100% and 0%, i.e. 33. 333...% Looks logical to me but am I oversimplifying the problem?
It happened also to me. Now I was looking towards the community comments and I freak out a bit because I just faced the problem with intuition (I don't know how to compute integrals)
At 1/4 and 3/4, the overlap is 25%. This yields a sequence of 0%, 25%, 100%, 25%, 0%, and its average is not 33.333...%. It's 30%. So this doesn't work.
Log in to reply
The sequence can also be 0%, 100%, 0%, and the average is 1/3. That was my reasoning, but maybe it was pure randomness. Thank you for replying anyways.
Simply taking <x^2> from 0 to 1, gives us the required Answer=(1/3)
It suffices to find the average until the squares coincide. If the corner of each square has moved a distance t along the diagonal, the overlapped area is one half times the product of the diagonals ( which have length 2t) which is 2 times t squared. If we integrate this from 0 to the square root of 2 divided by 2 and divide by the square root of 2 divided by 2 we get one third
At the beginning of the animation, the red square is in the top right corner. At this specific time, the area of overlap between the two squares is 0. Halfway along its path, the red square and blue square completely overlap. 100% of the red square is on the blue square, so 1 1 , or 1 of the square overlaps. Lastly, when the red squares reaches the bottom left, the area of overlap between the two squares is 0. Taking the average of 0, 1, and 0 across these three time interveals yeilds 3 1
I cheated, just a little. First I assumed that the squares move at constant speed. Now, the integrand is obviously the square of something, and integrating it will yield a third of something else. There was just one answer that had a 3 in the denominator.
Instead of the case when both squares are moving, consider the case when only one is moving twice faster and the other is stationary. Since the square is moving along the diagonal, we have Δ x = Δ y .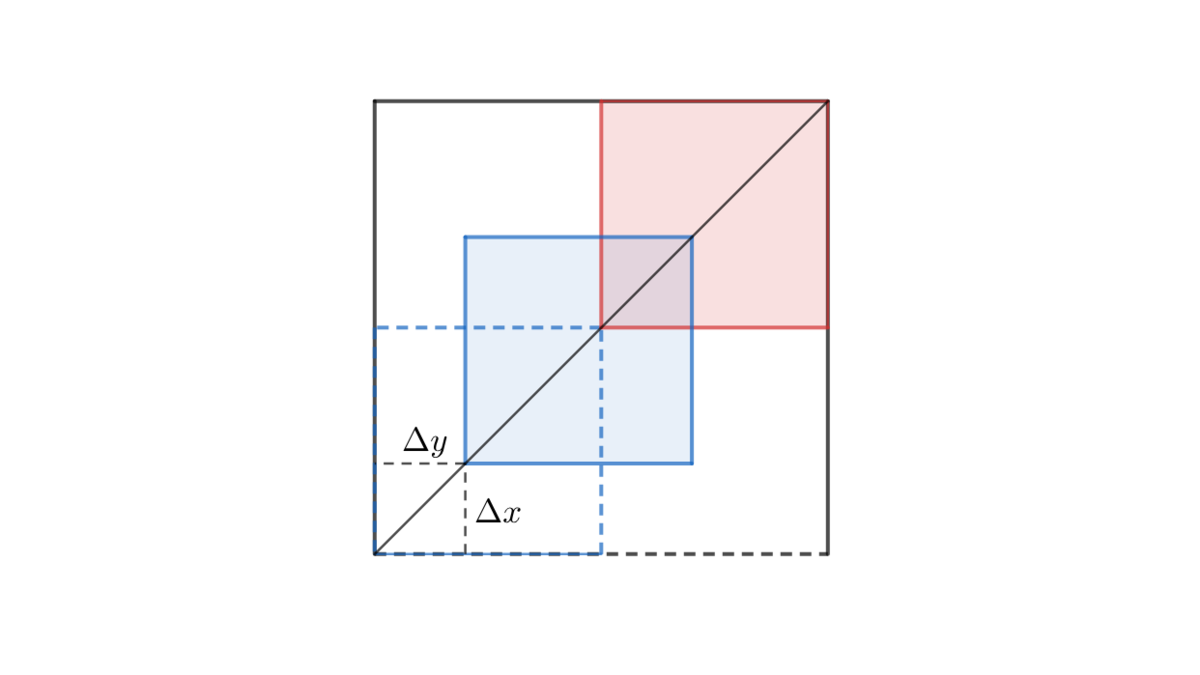
The average area of overlap is then:
∫ 0 1 x 2 d x = 3 x 3 ∣ ∣ ∣ ∣ 0 1 = 3 1