Slip Less!
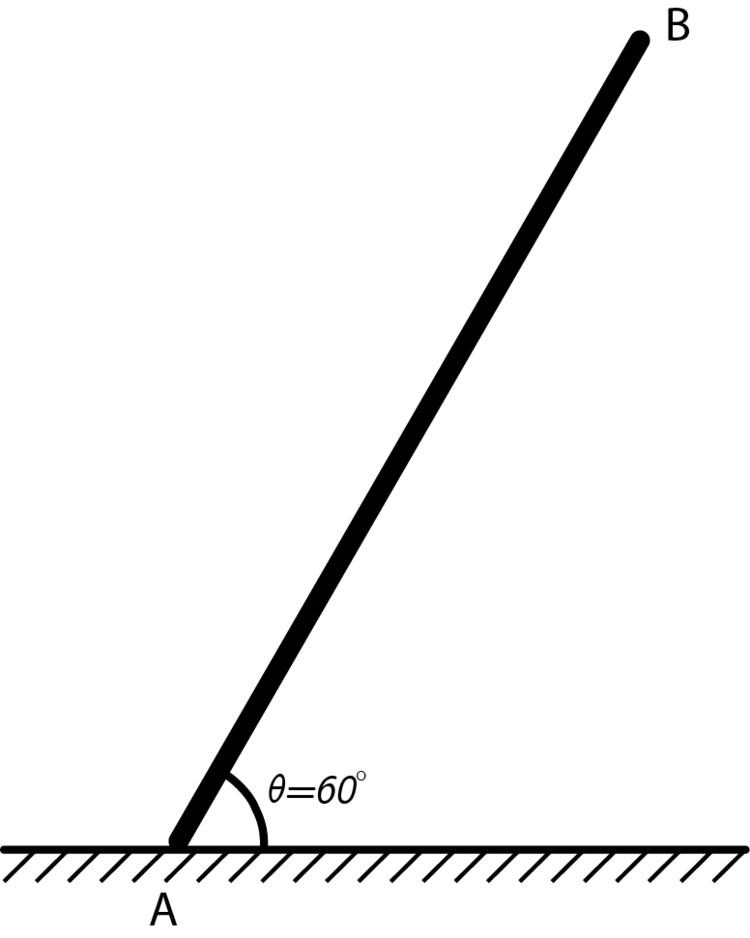 Find the minimum static coefficient of friction
μ
s
between a rod and the surface so that the rod, which when released from rest does not slip at the instant it is released.
Find the minimum static coefficient of friction
μ
s
between a rod and the surface so that the rod, which when released from rest does not slip at the instant it is released.
Note: the rod is released from rest inclined at an angle θ = 6 0 ∘ .
The answer is 0.3997.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
This is an exceptional solution. Your diagrams are very clear and your argument is as concise as it gets.
yea.. did it in d same way..
Log in to reply
this question i found in my package
Log in to reply
It is there! Rotational Mechanics Phase 3
Oh really... well.. good then!
Some doubt,
Let there be a mass m on the rod and the coefficient of friction be μ . The acceleration towards the ground would be m g sin 6 0 o and frictional force be μ m g cos 6 0 o . I think to minimize slipping acceleration should be 0 . Thus giving μ = tan 6 0 o = 1 . 7 3 2
Log in to reply
typo.. acceleration should be g sin60. Anyways.. can u tell me y it should be so? You dont know the value of N and without that how would u calculate acceleration of COM of the rod, except for writing torque equation...
first of all normal reaction wouldnt be mg cos60,it would be mg
Log in to reply
No, it would not because it has a downward acceleration.
Log in to reply
@Kishore S. Shenoy – N always acts perpendicular to the surface.therefore it should be mg. yhowever as the rod does not move..
Log in to reply
@Kaustubh Miglani – No. See this :
The Normal N acts on the centre of mass. You know that the centre of mass is moving downward also. If, as you said, N = m g , then the cenre of mass sould not move down, which is wrong. Thus N < m g .
No. You can't just predict that. You have to first consider it as N
Could you please tell me how you got the force 2 l α on the COM and what force it is?
Log in to reply
Since the rod is rotating about the contact point with α angular acceleration, the net force acting on the centre is l e n g t h f r o m a x i s × α = 2 l α
Log in to reply
Sorry, but I still didn't understand. Why should the force acting be l e n g t h x α ? Could you please explain how you got it? Sorry for the doubt, but I've just started learning Rotation and am quite confused.
Log in to reply
@User 123 – See. The basic definition of radians is that Radius × Angle = Arc Length . Differentiating twice, Radius × α = a [ linear ]
So here, at centre of mass which is at a distance 2 l from the point of contact, linear acceleration is
[ Linear ] a = 2 l α
Hope you understand! Do ask if any doubts occur! Well I'm also studying rotation right now! It's in Phase 3. You're in FIITJEE right?
Log in to reply
@Kishore S. Shenoy – Yeah, I understood. Thanks very very much! Actually I had forgotten that r ω = v and r α = a ! Yes, but we're still in Phase 2 and have just started COM. By the way, Rotation is the last chapter of Phase 2 for us.
Log in to reply
@User 123 – Oh is it! We're now Phase 3 right now.
@Kishore S. Shenoy – Hey..im A FIITJEE student as welll... Chennai Kilpauk Centre
@Kishore S. Shenoy – One last doubt please. What is causing the force on the C M ? Is it friction?
Log in to reply
@User 123 – @Ishan Dasgupta Samarendra When I took accelerations of centre of mass, I am taking it w.r.t ground. Hence we can consider N to be acting at C M . But if we are taking w.r.t any point on the system, we have to consider τ torques only (including that due to pseudo forces, that act at CM). If we consider any point on the rod, we get no solution. So I used linear system.
@User 123 – @Ishan Dasgupta Samarendra When I took accelerations of centre of mass, I am taking it w.r.t ground. Hence we can consider N to be acting at C M . But if we are taking w.r.t any point on the system, we have to consider τ torques only (including that due to pseudo forces, that act at CM). If we consider any point on the rod, we get no solution. So I used linear system.
Well @Ishan Dasgupta Samarendra , In rotation, for a body undergoing general plane motion, you can always assume a body to TRANSLATE with some VELOCITY and ACCELERATION and ROTATE about a particular point with some ANGULAR VELOCITY and ANGULAR ACCELERATION. Now for any other point on the body the velocity and acceleration is given as the vector sum of TRANSLATION and ROTATION part.
Hope that it helps
How did you solve it. Any other method? Please Share.
Log in to reply
Alright, but later. My exams are going on and my method was quite tedious.
I do not still understand what you mean in Collisions Galore! . 10 t h means that between wall and ball right?
Log in to reply
10th collision between the ball and the block. Hope you like the problem:)
Log in to reply
@User 123 – Only considering the collisions b/w the block and ball? That calculation is tough! There should be some easy method!
Log in to reply
@Kishore S. Shenoy – Yeah. Well, hopefully you'll come up with one!
You must specify the direction of acceleration of the rod's COM. By what I mean that you need to tell why rod's COM will have acceleration normal to the rod. Actually, I am saying so because it took me quite a time to get the direction. :P I was messing around with hazard(a lot of puns, hint:football).
Log in to reply
Normal to the rod. Not surface
Log in to reply
Yeah sorry. Actually I meant normal to the surface of the rod. It has become so usual to say "normal to the surface". That's why I got it. Edited!
But the application point of friction is at the bottom so why did you consider its torque???(at COM) Plz clarify my doubt... @Kishore S Shenoy
How are you so awesome in physics, Can you please suggest me some tips for physics problem solving?
Thanks!
Could someone please point out the mistake in my reasoning?
The acceleration of the bottom end of the rod is 0. So forces are in equilibrium. The forces are tension, T, from the rod, friction, f and the normal force, N.
Resolving forces vertically: N = ( 3 / 2 ) T . Resolving forces horizontally: f = ( 1 / 2 ) T .
Therefore N = 3 f , so μ ≥ 1 / 3
Log in to reply
Forces act at the centre of mass rather than any other point. To elaborate this, consider a ring of mass in the vertical plane, i.e. its axis is parallel to the ground, and is touching the ground at exactly one point. Now, we push the topmost point of the ring to gently make it roll about its own axis. We know that the lowermost point will not slip, but the net force on the lowermost point is the frictional force. This contradicts Newton's Second Law. This is because forces act at the centre of mass of the body when we consider net forces. The geometry of the object plays a role in angular mechanics only. At the centre of mass, the force we provide to roll the ring counteracts the frictional force and Newton smiles in his grave. Hope this helped!
I think I see my mistake. The internal forces in the rod need not be parallel to the rod.
There is a serious mistake.While writing the equation for vertical motion you just took the component of tangential acceleration along vertical direction and missed out the component of normal acceleration along vertical direction.Please see this carefully https://www.youtube.com/watch?v=0igjzb5JSLE.
Log in to reply
There! I got it! The question asks about and only about the instant when it starts rotation. There ω = 0 .
Log in to reply
Clever boy :-D.I did'nt notice that "instant" part.How one word can change so many things :-P!
But please modify the question saying it is released at 60 degrees angle...
Can you explain where? I did not understand what you meant... ☺
Log in to reply
You did'nt consider the component of centripetal acceleration in y direction.You just took tangential acceleration.Check the video I linked.
For a general theta i found the solution as u=3sinx.cosx/(1+3sin^2(x)) where x=theta.
Great! I never thought of it.
Seems nice. Put x=90 . Another good part.
Taking Torque about A,
τ = m g 2 l cos θ = 3 m l 2 α
⇒ α = 2 l 3 g cos θ = 4 l 3 g
α = 4 l 3 g ⋯ ( 1 )
Taking Forces at Centre of Mass, (since forces act on the centre of mass)
Acceleration of centre of mass is perpendicular to the rod because it is performing a pure rotation about the point of contact. a = α × r
m α 2 l cos θ ( 1 ) ⇒ 1 6 3 m g N = m g − N = 1 6 1 6 m g − N = 1 6 1 3 m g
Applying F = m a for the horizontal forces:
μ N i.e μ 1 6 1 3 m g = 2 m α l sin θ = 1 6 3 3 m g
⇒ μ s = 1 3 3 3 ≈ 0 . 3 9 9 7