Slippery Chain!
A uniform chain of length
ℓ
is released from rest on a smooth horizontal table with a portion
h
of the chain overhanging as shown in the figure. Find the time taken by the chain to just slip off the table.
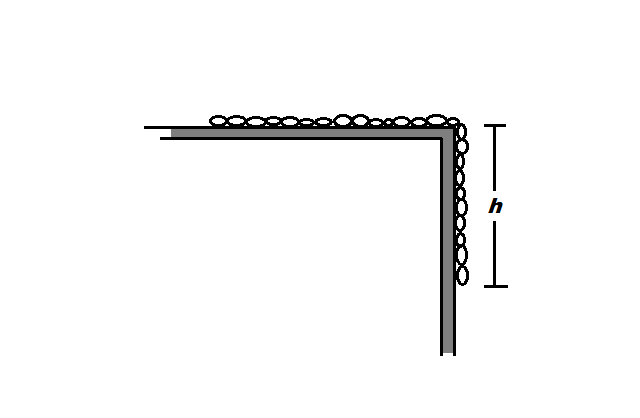
Details and assumptions :
- As already stated, the surface of table and links of chain are smooth and there is no friction between links of chain and the table or in between the links of the chain.
- The chain will just slip off when the left most end of the chain reaches the edge of the table.
- The chain possesses some mass which is not negligible.
- The answer should be in seconds.
If you liked this problem, why don't you try another one ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions


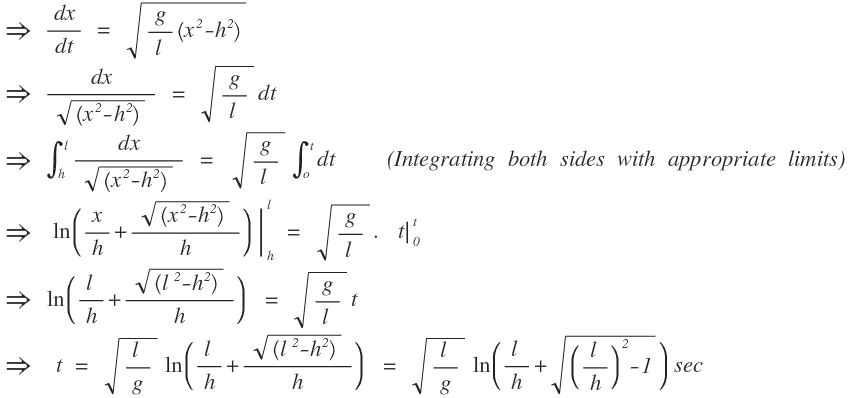
The velocity equation may be derived directly from conservation of energy.
Thanks mate. Just used the elementary approach. :)
Just saying.. If such a long question comes in objective exams please don't solve it to waste your... If you put H=L time should come out to be 0 and putting H=0 should give time as infinite which leaves only one option. Great solution by tapas though.
Log in to reply
you have a great mind !
*waste your time
Beautifully explained solution with a very clear approach. Well done. :)
I am sorry but how do you integrate integral1/sqrt(x^2-h^2) dx
Log in to reply
Put u = h x which means that d u = h 1 . Now I = ∫ u 2 − 1 1 d u . Then put u = sec t which means that d u = sec t . tan t . d t Again I = ∫ sec 2 ( t ) − 1 sec ( t ) tan ( t ) d t = ∫ sec ( t ) d t Solving for I you would get → I = ln ( tan ( t ) + sec ( t ) ) . Now substitute all the variables to get the original ones back, to get the result, I = ln ( ∣ ∣ ∣ ∣ ∣ h 2 x 2 − 1 + h x ∣ ∣ ∣ ∣ ∣ ) + C
Why have we taken the limits during the integration of the velocity equation from h to x
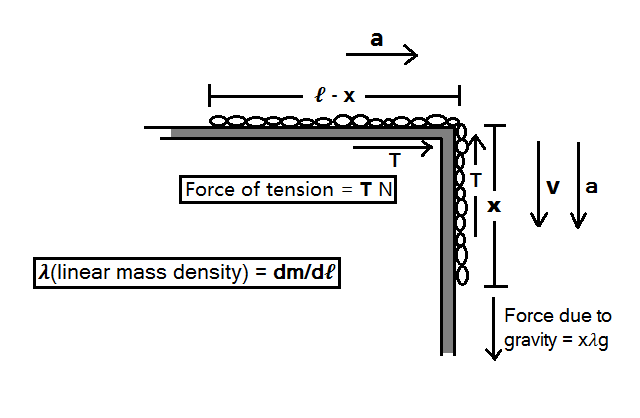
Let x ( t ) be the displacement of the chain at time t . Then at any time t the external force on the chain is F = σ ( h + x ) g , where σ is mass per length of the chain and g is acceleration due to gravity. This force F is used to accelerate the whole chain F = σ l d t 2 d 2 x . Therefore, we have:
σ ( h + x ) g d t 2 d 2 x = σ l d t 2 d 2 x = l g x + l g h
The general solution for the differential equation is as follows:
x ( t ) x ( 0 ) ⟹ c 1 + c 2 d t d x ∣ ∣ t = 0 ⟹ c 1 = c 1 e l g t + c 2 e − l g t − h = c 1 + c 2 − h = 0 = h . . . ( ∗ ) = c 1 − c 2 = 0 = c 2 = 2 h Note that x ( 0 ) = 0 Also that d t d x ∣ ∣ t = 0 = 0 ( ∗ ) : c 1 + c 2 = h
⟹ x ( t ) = 2 h ( e l g t + e − l g t − 2 )
When the chain slips off the table at t 1 , x ( t 1 ) = l − h , then,
2 h ( e l g t 1 + e − l g t 1 − 2 ) 2 h ( e l g t 1 + e − l g t 1 ) e l g t 1 + e − l g t 1 ( e l g t 1 ) 2 − h 2 l e l g t 1 + 1 = l − h = l = h 2 l = 0 Multiply throughout by e l g t 1 A quadratic equation of e l g t 1
⟹ e l g t 1 t 1 = h l ± ( h l ) 2 − 1 = g l ln ⎣ ⎡ h l + ( h l ) 2 − 1 ⎦ ⎤
ln ⎣ ⎡ h l − ( h l ) 2 − 1 ⎦ ⎤ < 0 and it leads to negative time, which is unacceptable.
The differential equation can be obtained by conservation of energy (in the absence of friction, both internal and external, this is fine). The kinetic energy of the chain is 2 1 m x ˙ 2 , while the potential energy of the chain is − ℓ x m g × 2 1 x = − 2 ℓ m g x 2 and hence 2 1 m x ˙ 2 − 2 ℓ m g x 2 = − 2 ℓ m g h 2 leading to x ˙ 2 = ℓ g ( x 2 − h 2 ) After this, solving the differential equation proceeds normally.
Why did you use the kinetic energy of the whole chain, instead of the portion that hangs down? Using the same technique that you showed in the solution to the other problem (faster than gravity), you should have set the kinetic energy to 1/2 x'^2 (m x/L) instead of 1/2 x'^2*m. The solution would be different from the one stated, but perhaps the stated solution is wrong (as the energy is not conserved) ?
Log in to reply
In this problem, the whole chain is moving. The portion of the chain on the table is moving horizontally, the portion of the chain that is hanging down is moving vertically.
In the other problem, the left-hand side of the chain is stationary, since the point A is fixed.
Log in to reply
Thanks for your reply. I think I see why the whole chain needs to be taken in the account here. But in the other problem, even though the point A is fixed, the center of mass of the left-hand side is actually moving. This is bothering me, as I'm not able to convince myself the solution is correct. I should be able to calculate the kinetic energy of the system by using the square of the velocity of the center of mass of the whole system times half the mass. Why is it not the case?
Log in to reply
@Ilya Lyubarsky – I hope I have pointed out the problems with your argument in the Faster than Gravity discussion...