Slippery Pulley!
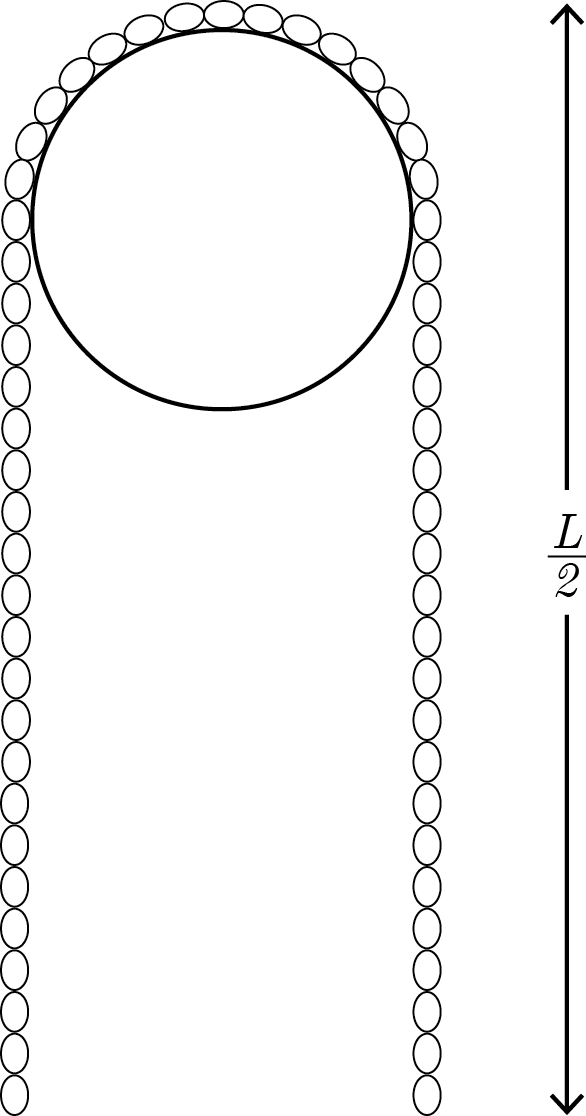
A heavy, long, inelastic chain of length L is placed almost symmetrically onto a light pulley which can rotate about a fixed axle, as shown in the figure. If :
I ) It's velocity when it leaves the pulley can be represented by v b r e a k = y L w g x
II ) And height h climbed by the end which is going up before losing contact of the pulley can be represented as h b r e a k = z L
Evaluate 2 w + x + y + z + 1
Assumumptions
- Take the pulley to be massless and thus performing pure rolling.
- The chain goes up due to slight asymmetry.
- w , x , y and z are numerical constants ∈ R and can have any value!
- Take radius R of the pulley to be very small, i.e. R ≪ L
The answer is 6.328427.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Kishore S Shenoy did the same way. Give us time to post solutions to ur problems. What's the fun in posting solutions to ur own problems. When's ur next problem coming? Me and @Surya Prakash will try to post the solution.
Log in to reply
Hehe, sure! I post solutions so that those who were unable to solve will get a way... Wait for some time... Be patient
P.S: I will get upvotes 😜
Log in to reply
Sure! But please give us time to post solutions. :)
Log in to reply
@Aditya Kumar – Just refresh the page to see the updated comment
Log in to reply
@Kishore S. Shenoy – I meant to say more time.
Log in to reply
@Aditya Kumar – I understood...
@Aditya Kumar – But upvotes matter...
Log in to reply
@Kishore S. Shenoy – So u mean to say u r posting questions and solutions just for popularity. If u want upvotes post solutions to easy problems.
Log in to reply
@Aditya Kumar – Nope... I post solutions for tough questions only. If you post for easy ones, you'll get lots of upvotes which has no value...
Log in to reply
@Kishore S. Shenoy – Then how do upvotes matter?
Log in to reply
@Aditya Kumar – It's like it encourages me to put more questions... 😊
@Aditya Kumar – Try solving my math questions...
Log in to reply
@Kishore S. Shenoy – Saw them. Did u try my problems?
Log in to reply
@Aditya Kumar – No! I'll for sure!
@Aditya Kumar – I'll be posting a question today! Designing it!
Log in to reply
@Kishore S. Shenoy – Sure. But let me post a solution.
though i got the correct answer but it was a little bit confusing as no relation was given between y and z. I advise you to remove variable y from question and write it as 1 only.
Hey @Kishore S Shenoy when the chain is about to lift off from the pulley its N = 0 so we get 2 forces for a d m mass element which provide the centripetal force at that instant the forces are 2 T sin ( 2 d θ ) which we used but why did we ignore the component of force of gravity in that direction d m × g cos ( 2 d θ ) ? Please tell if i am going wrong somewhere
Log in to reply
Actually, when the chain leaves the pulley, it is a vertical straight line, so that the relative accelerations between two infinitesimally small mass element is zero, ie. gravitational force does not produce internal tension. Thus the only force that provides centripetal acceleration is tension. Hence T ( i ) = ρ v 2
Log in to reply
Btw how do you draw the diagrams for the questions?
@Kishore S Shenoy When one end goes up a distance of x , the other end goes down by a distance x . So, shouldn't Δ P E = 0 ?
Log in to reply
Log in to reply
Thanks for the pic! I should've taken the centre of mass then there wouldn't have been any issue. My bad.
Log in to reply
@Deeparaj Bhat – Yeah, that's the basic idea.
@Surya Prakash Can you post your solution please?
Log in to reply
Did the same. I failed to solve the problem ALL THAT MATTERS IS THE CONSTANT VELOCITY. Then I solved this problem by learning the concept from the solution of that problem.
Log in to reply
It was meant for this same reason!
Log in to reply
@Kishore S. Shenoy – Hey man, do u have account in Brilliant Slack??
Log in to reply
@Surya Prakash – Slack? What is it? Why?
Log in to reply
@Kishore S. Shenoy – slack . It is chatting platform where we can chat. Brilliant members are present there. Make an account in it. Come over there.
Log in to reply
@Surya Prakash – Can you say how to join?
Log in to reply
@Kishore S. Shenoy – just go to slackin.brilliant.org and type your email and submit it. You will get a mail to your email. Then follows according to that what it says. That's it.
Log in to reply
@Surya Prakash – I'm already invited! I did not know!
@Surya Prakash – I'm there!
From the question All that matters is the constant velocity! , we know that once the chain is out of the pulley, T = ρ v 2 ⋯ ( 1 )
Now when one side of the chain goes a height x , △ P E = △ K E ρ x 2 g = 2 1 ρ L v 2 ⇒ L v 2 = 2 x 2 g ⋯ ( 2 )
Now equating forces
T − ρ ( 2 L − x ) g = ρ ( 2 L − x ) a ⋯ ( 3 ) ρ ( 2 L + x ) g − T = ρ ( 2 L + x ) a ⋯ ( 4 )
Solving L v 2 = 2 L 2 g − 2 x 2 g ⋯ ( 5 )
Substituting ( 1 ) , ( 2 ) in ( 5 ) , h b r e a k = 2 2 L
v b r e a k = 2 L g
⇒ v = w = 0 . 5 , x = 2 , y = 1 , z = 2 2
∴ 2 v + w + x + y + z ≈ 6 . 3 2 8 4 3