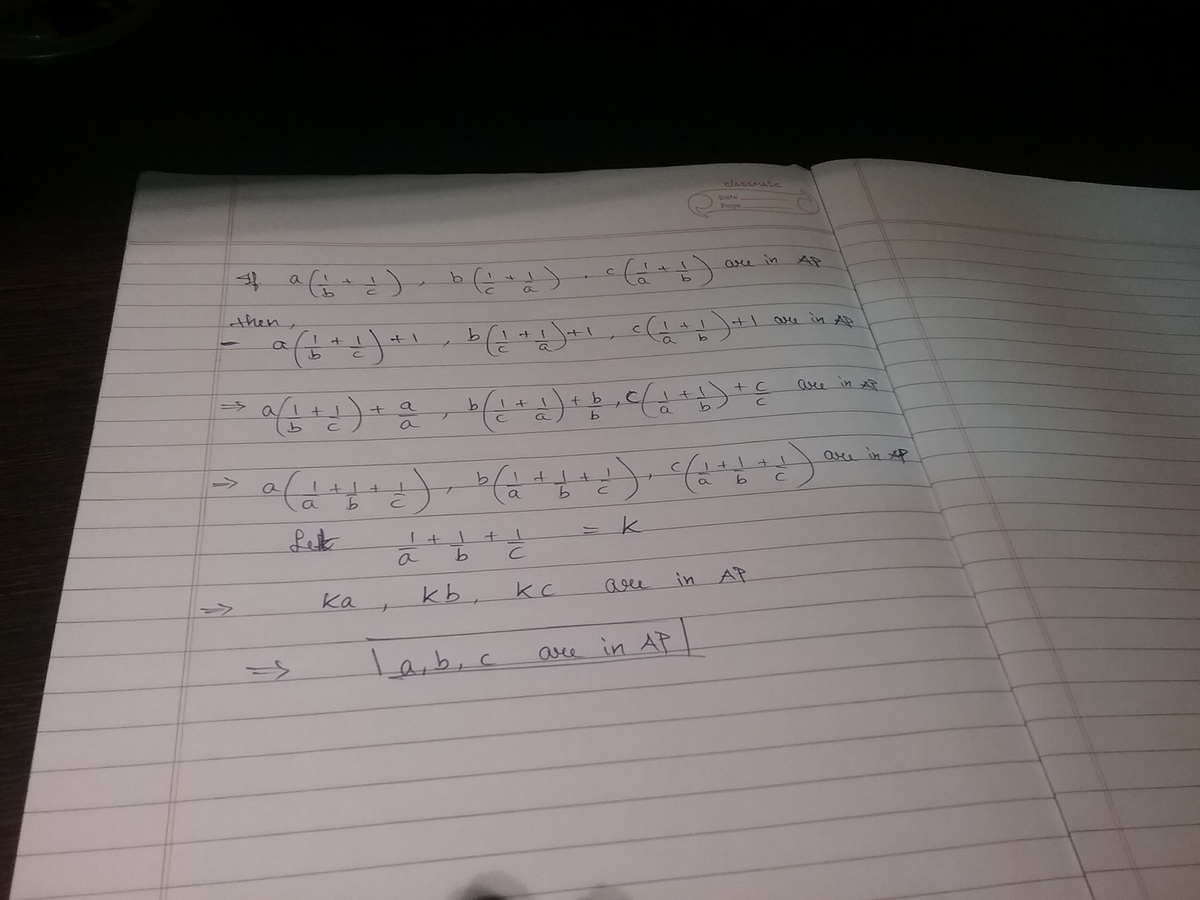Slow and Steady wins the race...
a ( b 1 + c 1 ) , b ( c 1 + a 1 ) , c ( a 1 + b 1 )
Given that the above three numbers are in an Arithmetic Progressions (AP).
Then which one of the following is true?
Details and Assumptions:
∙ GP corresponds to Geometric Progressions
∙ HP corresponds to Harmonic Progressions
∙ AGP corresponds to Arithmetico-Geometric Progressions
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
To start, I will use a property of triplets in arithmetic progression: a ( b 1 + c 1 ) + c ( a 1 + b 1 ) = 2 b ( c 1 + a 1 ) . Multiply through by a b c , and rearrange the terms to get 2 ( a + c ) b 2 − ( a 2 + c 2 ) b − a c ( a + c ) = 0 ⇒ b = 4 ( a + c ) a 2 + c 2 ± a 4 + 2 a 2 c 2 + b 4 − 8 ( − a c ) ( a + c ) 2 ⇒ b = 4 ( a + c ) a 2 + c 2 ± a 4 + 8 a 3 c + 1 6 a 2 c 2 + 8 a c 3 + c 4 = 4 ( a + c ) a 2 + c 2 ± ( a 2 + 4 a c + c 2 ) = 2 a + c , − a + c a c The solution b = − a + c a c implies a 1 + b 1 + c 1 = 0 , which, in turn, implies the common difference is b ( c 1 + a 1 ) − a ( b 1 + c 1 ) = b ( − b 1 ) − a ( − a 1 ) = − 1 + 1 = 0 . So, for example, a = 1 , b = − 2 , c = − 2 gives a constant sequence for a ( b 1 + c 1 ) , b ( c 1 + a 1 ) , c ( a 1 + b 1 ) because 1 − 2 1 − 2 1 = 0 , but the sequence a , b , c is clearly not arithmetic. So, I must add the assumption that the original sequence is not constant. The other solution b = 2 a + c is equivalent to a + c = 2 b , which allows us to conclude a , b , c are in arithmetic progression.
Umm... nice approach... but you think this much hard work is required? Looks like there are pretty good chances of making simplification mistakes(to me)...
Log in to reply
Yes, it's definitely more work than necessary. However, I figured, in terms of solutions, the more, the merrier. Nice job on your solution, by the way. Very clever.
Log in to reply
Hahaha! Thanks a lot for the appreciation!
Please don't take my previous comment otherwise... I wasn't criticizing your solution at the slightest...I just meant it's a bit long that's all...
Log in to reply
@Skanda Prasad – You're welcome. No offense taken. ;)