Slow down there, you silly piece of metal
A square loop of metal of side length L = 0 . 1 m , mass m = 0 . 1 kg , and resistance R = 1 Ω , oriented in the x y plane, is traveling to the right (positive x direction) at a speed of v 0 = 0 . 1 m/s . At time t = 0 , the right edge of the loop enters a region of magnetic field B = 1 z ^ T . At what time in seconds does the left edge of the loop enter the magnetic field?
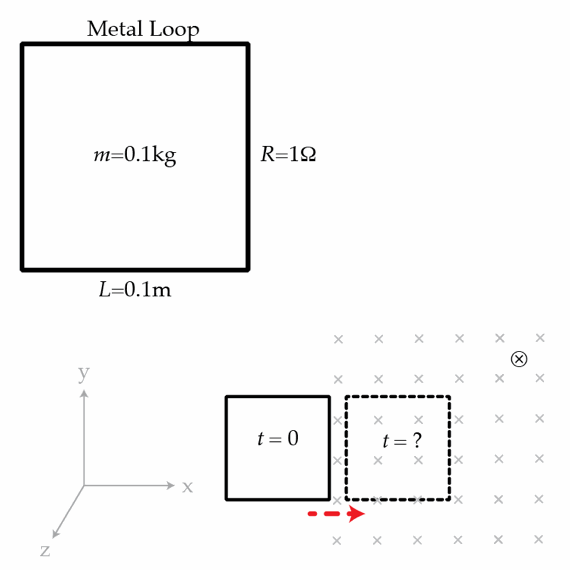
The answer is 1.054.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
liked
I used the same way on my second attempt. On my first attempt, I tried to compensate the loss of heat i^2rt with 1/2mv^2, but could not reach to the solution. I am still wondering what went wrong on the first attempt. Can you help me?
Log in to reply
Hi Kaustav!
In your first approach, you seem to assume that the loop has zero velocity when it is completely inside the magnetic field. You might have noticed that this is wrong when you used the second approach.
The second error is that the loss of heat is not given by i 2 R t . Actually, it is given by ∫ 0 t i 2 R d t = ∫ 0 t R ε 2 d t .
So, applying energy conservation, we end up with: 2 1 m v 0 2 = ∫ 0 t R B 2 l 2 v 2 d t + 2 1 m v 2
Differentiating both the sides wrt t,
0 = R B 2 l 2 v 2 + m v a
Substituting the values, we end up with
a = − 1 0 v
which is the same result as before.
I hope that helped.
Log in to reply
Thanks Pranav, It really helped me a lot. Now I figured out where I went wrong. Huh, except for the integration part of I^2Rdt, I did everything else the correct. This problem was driving me crazy till the F=BIL striked. Thanks again.
Can someone please fix a small typo? I did not intend to write "The direction of current is determined". Can someone please remove it? Many thanks!
We start off by calculating the flux through the square loop, Φ B = ∬ S B ⋅ d S . We have Φ B = ∫ 0 L ∫ 0 x B d x d y , where x = x ( t ) . This results in Φ B = B L x ( t ) . Now we can use Faraday's law to determine the potential, V = − ∂ t ∂ Φ B = − B L v , where v = v ( t ) . We can that there will be a force acting on the loop, since there will be a magnetic force acting on the part that is within the magnetic field, given by F = I ℓ × B Using Ohm's law, we can relate the current and the potential (or voltage), V = I R . So subbing everything into our equation, we find that m a = − R B 2 L 2 v . To simplify our calculations, let Q = m R B 2 L 2 . Thus we have a first order differential equation, d t d v = − Q v . We can simply use separation of variables to obtain v = v 0 e − Q t where v 0 appears as an initial condition. So now we can integrate again to determine x = x ( t ) , so x ( t ) = − Q v 0 ( 1 − e − Q t ) where we used the initial conditions x ( 0 ) = 0 . Inverting our function, we can easily calculate for t ( L ) . t ( x ) = − Q 1 ln ( 1 − v 0 x Q ) . Finally, t ( L ) = − Q 1 ln ( 1 − v 0 L Q ) = − L 2 B 2 m R ln ( 1 − m R v 0 L 3 B 2 ) = 1 . 0 5 4 s .
First, let's try to find the direction of the magnetic force on the metal plate. This is easily doable by the right hand rule. Look at the following picture:
 In case the image doesn't load, go to: http://s22.postimg.org/pjyr5yjmp/Untitled.png
In case the image doesn't load, go to: http://s22.postimg.org/pjyr5yjmp/Untitled.png
The magnetic force is directed opposite to the velocity of the plate. Now, consider a moment of time when the metal plate is at a distance x into the magnetic field. See the following diagram:
 In case the image doesn't load, go to: http://s13.postimg.org/6i2e9a5qf/Untitled.png
In case the image doesn't load, go to: http://s13.postimg.org/6i2e9a5qf/Untitled.png
The area of the plate under the magnetic field is A = L x . The magnetic flux going through this plate is given by ϕ = B × L x cos ( 1 8 0 ∘ ) = − B L x Let ϵ be the induced EMF in the conductor. From Lenz's law, we know that ϵ = − ∣ ∣ ∣ ∣ d t d ϕ ∣ ∣ ∣ ∣ Note that ∣ ∣ ∣ ∣ d t d ϕ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ d t d ( − B L x ) ∣ ∣ ∣ ∣ = B L × d t d x = B L v where v is the velocity of the metal loop. The induced EMF will then be: ϵ = − ( − B L v ) = B L v The current induced in the metal loop can be found from Ohm's Law: i = R ϵ = r B L v Recall that the Lorentz force acting on a body with charge q , velocity v , in a magnetic field of magnitude B (and in an electrically neutral field) is given by: F = q v × B We can rewrite v as t L (where L is the length of the conductor, and t is the time taken for the particle to travel across the conductor). We have: F = q t L × B = t q L × B = i L × B Recall the expression for i we got earlier: i = r B L v Plugging this value, we obtain: F = r B L v L B sin ( 9 0 ∘ ) = r B 2 L 2 v As we found out earlier, the force is directed opposite to the velocity, so we get the differential equation − m d t 2 d 2 x = r B 2 L 2 v ⟹ − m d t d v = r B 2 L 2 v ⟹ d t d v = − r m B 2 L 2 v Let k = r m B 2 L 2 Then, d t d v = − k v We have the initial condition v ( 0 ) = v 0 . Solving this differential equation, we obtain v ( t ) = v 0 e − k t Now we again write v as d t d x , so we have another differential equation: d t d x = v 0 e − k t With the initial condition x ( 0 ) = 0 , we obtain x ( t ) = k v 0 − v 0 − k t We now have to solve the equation k v 0 − v 0 − k t = L for t . This can easily be done, yielding t = k lo g ( m − k L m ) Plugging in the values from the question yields t ≈ 1 . 0 5 4 s .
So to start let us assume that the velocity of loop be v l and the emf induced by E so by Faraday's law of electromagnetic induction we come to the general formula for the induced emf in time t for a conductor in motion as
E = v l B l
and then by Ohm's law we have E = I R or I = R E (1)
Putting the value of E in (1) we get the current I = R v l B l
It's pretty straightforward till here right ?
Now, if we analyze the motion we can see that the net force in the vertical direction is zero so F y = 0 while the force in the horizontal that is F x is retarding the motion. So now applying the equation of Lorentz force and plugging the value the value of I in it we get the force as
F n e t = − R v l B 2 l 2
Now if we closely look at the situation we can apply the Newton's Second Law as
m a = F n e t
m a = − R v l B 2 l 2
So after putting all the values in this we arrive at the equation
v l = − 1 0 a or a = − 1 0 v l
Now we also know that a = d t d v
Now putting this in above equation we get
d t d v l = − 1 0 v l
and then integrating between proper limits we get
∫ v 0 v l v l d v l = ∫ 0 t d t ⟹ v l = v 0 e 1 0 − t
and now again we have that v l = d t d x
So replacing v l we get
d t d x = v 0 e 1 0 − t
Again Integrating,
⟹ ∫ 0 0 . 1 d x = ∫ 0 t v 0 e 1 0 − t
⟹ v 0 = 1 − e 1 0 − t
Now at last putting v 0 = 0 . 1 m / s and
solving that equation we arrive at our answer as
t = 1 . 0 5 4 s e c o n d s
Huh, that was lengthy but we solved it so
Congratulations !
First we use Faraday's Law to find the induced voltage in the loop:
E = − N ∗ Δ t Δ Φ
N is the number of coils in our loop, conveniently equal to 1 . Φ is the magnetic flux through the portion of the loop in the magnetic field. Since the field is perpendicular to the loop:
Φ = A ∗ B = L ∗ x ∗ B
We will take x to be the horizontal displacement of the loop from the initial position. And since neither the magnetic field nor the size of the loop are changing with time, we can pull the constants out of our derivative:
E = − ( L ∗ B ) ∗ Δ t Δ x
Now we can use E to find the current:
V = I ∗ R
I = R V = − R L ∗ B x ′ ( t )
Now looking at the geometry of the problem, the current in the piece of the loop entering the magnetic field is perpendicular to that magnetic field, while the currents in the two pieces of the loop above and below flow in opposite directions and have no effect on the horizontal forces.
F = I ∗ L ∗ B = − R L 2 ∗ B 2 x ′ ( t ) = m ∗ a
x ′ ′ ( t ) = − R ∗ m L 2 ∗ B 2 x ′ ( t )
This is a differential equation in fairly standard (linear, homogeneous) form so I won't go into how to solve it. The solution for x ( t ) :
x ( t ) = Q c 1 e Q ∗ t + c 2
where Q = − R ∗ m L 2 ∗ B 2
v ( t ) = x ′ ( t ) = c 1 ∗ e Q ∗ t
v ( 0 ) = v 0 = c 1
x ( 0 ) = 0 = Q v 0 + c 2
c 2 = − Q v 0
x ( t ) = Q v 0 e Q ∗ t − Q v 0
Now we want to solve for the time at which x ( t ) = L :
Q v 0 e Q ∗ t − Q v 0 = L
t = Q l n ( 1 + v 0 L ∗ Q )
Substituting parameters we get t = − 1 0 ∗ l n ( 0 . 9 ) ≈ 1 . 0 5 4
he force acting is . F=-b2L2v/R F=ma so ma=-b2l2v/R a=-v/10 since a=dv/dt t will be equal to 1.054 seconds smile emoticon
Let at time t , the velocity of loop be v . The magnitude of emf induced in the loop at time t is B L v .
The current flowing in the loop is I = R B L v . Due to this current, a force acts on each side of loop. It can be easily seen that the net force on the loop in the vertical direction is zero. The force acting on the right side of loop is opposite to the direction of motion and thus retards the motion. The direction of current is determined
The force acting is F = − R B 2 L 2 v .
From Newton's Second Law,
m a = − R B 2 L 2 v
Plugging in the values,
a = − 1 0 v
Since a = d v / d t , we have
∫ v 0 v v d v = − ∫ 0 t d t ⇒ v = v 0 e − t / 1 0
Replacing v with d x / d t ,
d t d x = v 0 e − t / 1 0 ⇒ ∫ 0 0 . 1 d x = ∫ 0 t v 0 e − t / 1 0
⇒ 0 . 1 = 1 − e − t / 1 0
(I substituted v 0 = 0 . 1 m / s )
Solving the above equation, t = 1 . 0 5 4 s e c .