Small Oscillation
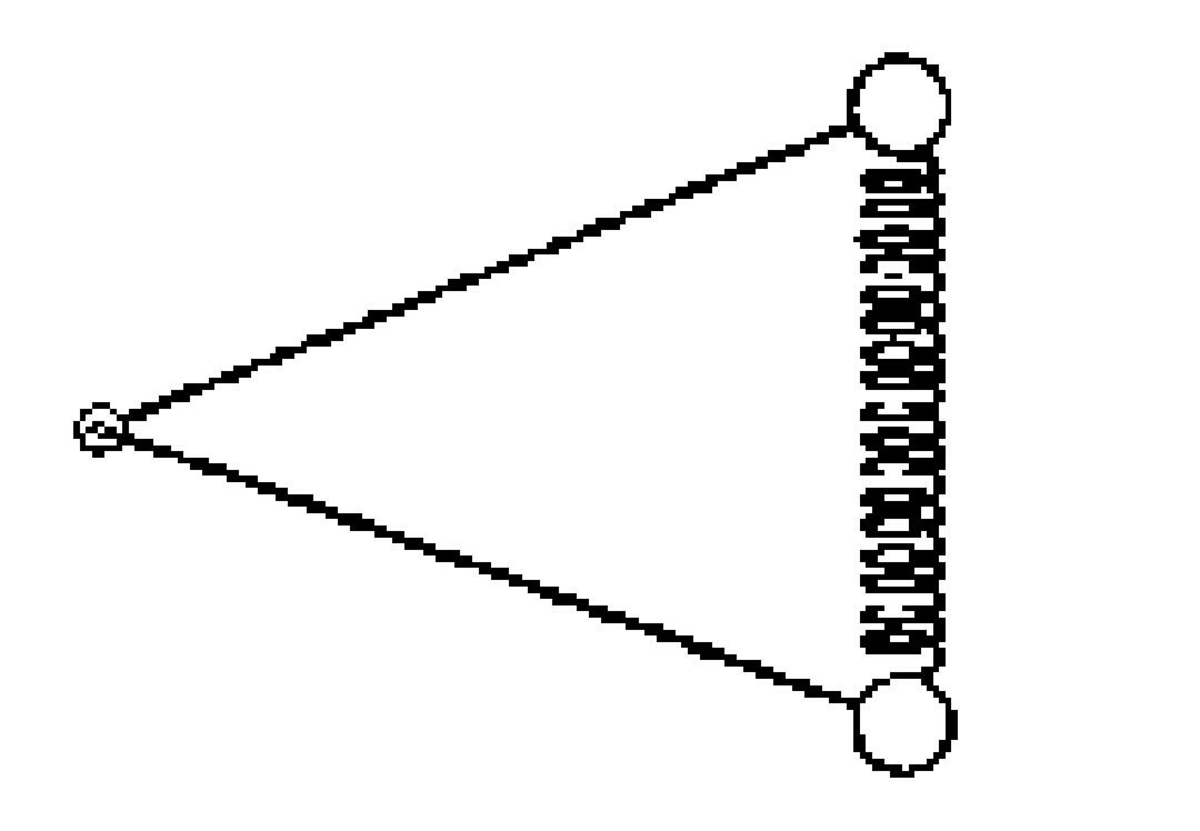 Two identical small discs each of mass
placed on a frictionless horizontal floor are connected with the help of a spring of force constant
.The discs are also connected with two light rods each of length
that are pivoted to a nail driven into the floor as shown in the figure by a top view.
Two identical small discs each of mass
placed on a frictionless horizontal floor are connected with the help of a spring of force constant
.The discs are also connected with two light rods each of length
that are pivoted to a nail driven into the floor as shown in the figure by a top view.
If period of small oscillations of the system is
Find relaxed length of spring.
Answer comes in the form of
Type
The answer is 1.414.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

Consider the origin of the X-Y plane to be placed at the pivot. The X-axis is horizontal to the right and the Y-axis points upwards. At any instant, let each of the rods make an angle θ with the horizontal. Therefore, the coordinates of each mass is:
x 1 = L cos θ y 1 = L sin θ
x 2 = L cos θ y 2 = − L sin θ
The kinetic energy of the system is:
T = m L 2 θ ˙ 2
The spring potential energy of the system is:
V = 2 k ( 2 L sin θ − L o ) 2
Where L o is the natural length of the spring. Lagrange's equation yields the following equation of motion. This can also be easily derived by computing the net torque experienced by a mass about the pivot. This working is left out of the solution. The equation of motion is:
2 m L 2 θ ¨ + 2 L k ( 2 L sin θ − L o ) cos θ = 0
Now, consider the system in equilibrium. Say the angle the rods make with the horizontal is θ o . Then, by using some elementary trigonometry, it can be seen that:
2 L sin θ = L o
Since we are considering small oscillations about this equilibrium, consider:
θ = ϕ + θ o
Here, ϕ is small enough so that the small-angle approximation holds good. That means:
sin ϕ ≈ ϕ cos ϕ ≈ 1
Plugging the above substitution in the EOM and simplifying gives:
m L 2 ϕ ¨ + ( 2 k L 2 cos 2 θ o ) ϕ = 0
The above equation represents SHM with natural frequency:
ω 2 = M 2 k cos 2 θ o
It is already given that:
ω 2 = M k
This implies that:
2 cos 2 θ o = 1
We know that
sin θ o = 2 L L o
⟹ 2 ( 1 − 4 L 2 L o 2 ) = 1 L o = 2 L