Small Raindrop
Consider the following model:
A raindrop falls from rest with a small initial mass, m 0 . As it falls, it accumulates mass by absorbing the smaller water drops in its path, which we approximate by the uniform density ρ atm .
Throughout the fall, it maintains the same characteristic shape defined by its width, 2 r , which increases as it picks up mass at the rate m ˙ = ρ atm π r 2 v (in time d t , it sweeps out a vertical cylinder of height v d t ).
How will its velocity depend on time? Surprisingly, this complicated problem has a simple solution: after a short time, the raindrop will accelerate at the constant rate a = K g (convince yourself of this!).
What is the value of K ?
Details and Assumptions:
- Neglect the effects of air resistance, wind speed, the density of air, or any other atmospheric factor except those stated in the problem.
Inspired by a similar problem by Tapas Mazumdar
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
You have added great physical insight and you solved a problem that is more difficult than the one I posted. Congratulations!
For the solution of the most general version of this problem, and for a review of the history of solutions, I recommend A. D. Sokal's paper, https://arxiv.org/pdf/0908.009
Log in to reply
Oh thanks! This paper is great (as is the problem, which I hadn't done before). I knew there must be a nice integrating factor floating around, but I went straight for the approximations when it didn't come to me.
that is amazing!
Respected senior Help me to get clear concept in the following question. A body is falling freely under gravity. How much distance it falls during an interval of time 1st and 2nd seconds of its motion taking g 10 m/s^2? a=10 m b=15 m c= 15 m d= 25 m
Log in to reply
I don't understand your question, are the a, b, c, and d different parameters?
Relevant wiki: Fluid Mechanics
First let us determine the mass as a function of time. Since we know that v = g t / K we can write
d t d m = λ m 2 / 3 K g t
or
m − 2 / 3 d m = ( λ g / K ) t d t .
Integrating this yields 3 m 1 / 3 = ( λ g / 2 K ) t 2 ,
m 1 / 3 = 6 K λ g t 2
Now we look at the equation of motion. We have to take into account that the droplets that are absorbed need to be accelerated to the velocity of the ball. Therefore m d t d v = m g is not enough, we have to add a second term:
m d t d v + v d t d m = m g .
We now insert the known functions to this equation:
K m g + K g t λ m 2 / 3 ( g / K ) t = m g
We divide with m and re-arrange:
K g + ( K g t ) 2 λ m − 1 / 3 = g
Notice that we have here an m 1 / 3 term that we have just calculated. Using that we get
K g + K 6 g = g
Therefore K = 7
Note: the mass of the raindrop increases as the 6th power of time, so the approximation we made in this solution will not be sustained for long.
Can you please elaborate on adding the second term $v/frac{dm}{dt}$ on why it adds up with the earlier term to give $mg$.
Log in to reply
Apologies I understand that it is by the chain rule of differentiating momentum(mv) with respect to time.
Log in to reply
It is a little more than the chain rule. The physics reason is that each time the raindrop hits and absorbs a smaller droplet, there is an inelastic collision that kicks the raindrop with an impulse backwards. Mathematically this process yields a term that looks like the chain rule.
Log in to reply
@Laszlo Mihaly – Or, much more simply, you consider the fact that force equals rate of change of momentum. At time t , there is mass m in the raindrop moving with speed v and mass δ m of water vapour, which is stationary. At time t + δ t there is mass m + δ m in the raindrop, which has speed v + δ v . Then ( m + δ m ) ( v + δ v ) − m v − δ m × 0 = m g δ t and so, dividing by δ t and letting δ t → 0 , we obtain d t d ( m v ) = m v ˙ + m ˙ v = m g
The raindrop reaches constant acceleration
The first thing to establish is the idea that the raindrop settles down to a constant rate of acceleration, which we can do with the following simple argument. At first, the raindrop experiences the net force F = m 0 g and therefore we have m 0 a = m 0 g ⟹ a = g , so that the raindrop experiences free-fall acceleration. As the raindrop builds mass, and therefore size, it collides with more and more stationary water droplets per unit distance, which it must accelerate from rest up to its current speed. Therefore, its acceleration will decrease with time.
Now, we don't expect the raindrop to start accelerating upward simply because it accumulates droplets. Therefore its downward acceleration either decreases to a constant, positive, finite value or it becomes zero.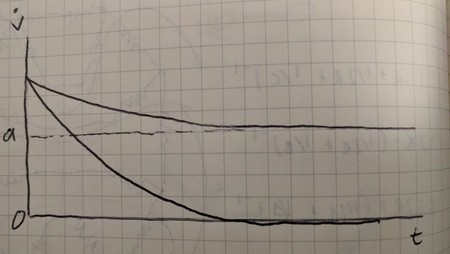 With these insights in hand we can start to analyze the physical model, staying open to both possibilities (
a
=
0
or
a
>
0
).
With these insights in hand we can start to analyze the physical model, staying open to both possibilities (
a
=
0
or
a
>
0
).
Physical model
As the problem suggests, the raindrop accumulates mass at the rate m ˙ = ρ atm π r 2 v . Since the raindrop maintains a constant shape, and its mass is proportional to its volume, we have m ∝ r 3 , or m = γ r 3 (for example, a sphere has γ = 4 π / 3 ) and thus m ˙ = α ρ atm m 2 / 3 v , where α is another constant.
At all times, the net force experienced by the rain drop is F = m g , which is equal to the time derivative of momentum p ˙ = m ˙ v + m v ˙ , and thus we have m g g = α ρ atm m 2 / 3 v 2 + m v ˙ = α ρ atm m − 1 / 3 v 2 + v ˙ To make progress, we can solve the mass accumulation equation to find m as a function of the displacement x . d t d m m 2 / 3 d m m 0 ∫ m m 2 / 3 d m 3 m 1 / 3 m = ρ atm α m 2 / 3 v = ρ atm α d t d x d t = ρ atm α 0 ∫ t d t d x d t = 3 m 0 1 / 3 + ρ atm α x = 2 7 ( 3 m 0 1 / 3 + ρ atm α x ) 3 This gives us the following illuminating form for the governing equation: g = 3 m 0 1 / 3 + ρ atm α x 3 α ρ atm v 2 + v ˙ If the acceleration decays to zero, then the velocity becomes a constant v ∞ and we have x = v ∞ t , so that at long times (when the v ∞ t term is large compared to 3 m 0 1 / 3 ), we have g ≈ ρ atm α t 3 v ∞ yielding v ∞ ≈ 3 t / g , which obviously does not satisfy v ˙ = 0 and so is not self-consistent. This shows that the acceleration must settle to some finite constant value a .
If a settles to a constant, we can apply the kinematic relation v 2 = 2 a x . We can find a if we wait until the raindrop has fallen a long distance, so as to ensure α ρ atm x ≫ 3 m 0 1 / 3 and therefore g = ρ atm α x 3 α ρ atm 2 a x + a = 7 a so that a = g / 7 .
Timescale of the switch
We can extract a bit more from the governing equation. At the start of the fall, the raindrop has uniformly acceleration a = g , but by the end it has acceleration a = 7 1 g . After how long, t switch , does this behavior switch?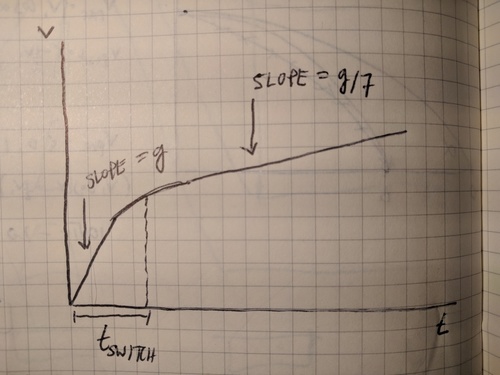 At early times,
v
is small and therefore the
v
2
term is approximately zero, yielding
v
˙
≈
g
,
as we noted earlier.
The point at which the behavior switches is when the term proportional to
v
2
becomes comparable to
g
,
e.g. when
g
≈
3
m
0
1
/
3
3
ρ
atm
α
v
2
.
At early times,
v
is small and therefore the
v
2
term is approximately zero, yielding
v
˙
≈
g
,
as we noted earlier.
The point at which the behavior switches is when the term proportional to
v
2
becomes comparable to
g
,
e.g. when
g
≈
3
m
0
1
/
3
3
ρ
atm
α
v
2
.
Replacing v with g t switch (which is valid before the switch), we find g ≈ m 0 1 / 3 ρ atm α g 2 t switch 2 or t switch ≈ 6 α 3 ρ atm 3 g 3 m 0 . Our simple prediction based on this argument is that the raindrop falls with a = g up until t switch after which it falls with a = 7 1 g . The graph below shows our cartoon model plotted in black, along the numerical solution plotted in blue (for m 0 = 0 . 0 1 k g , g = 9 . 8 1 m / s 2 , α = 1 ). For these numbers we have t switch ≈ 0 . 1 5 s .