Smallest Square Tangent to a Hyperbola
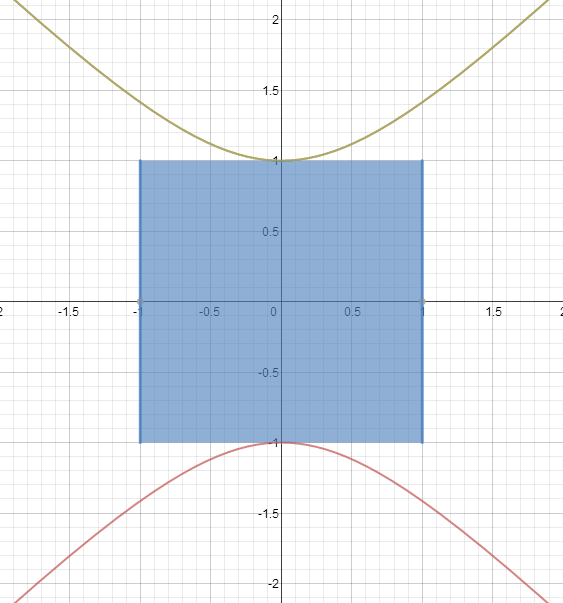
The smallest possible side length of a square who has 2 opposite sides that are tangential to the hyperbola y 2 = x 2 + 1 can be represented as 1 + S . What is ⌊ 1 0 0 0 S ⌋ ?
Details and Assumptions
The square given in the picture does not possess the shortest possible side length.
Having two opposite corners touch the hyperbola does not count as having the square tangent to it. The two opposite
sides
must be tangent.
The answer is 681.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Discussions for this problem are now closed
Let A , B , C , and D be the vertices of the square. Let A ( a , b ) where b = a 2 + 1 , then using rotation transformation of + 9 0 ∘ with the origin as the center of rotation, we get B ( − b , a ) , C ( − a , − b ) , and D ( b , − a ) . Using formula of distance between 2 points, we get A B 2 A B = ( a − b ) 2 + ( a + b ) 2 = 2 a 2 + 2 b 2 = 4 a 2 + 2 Now, using formula of distance between two paralel lines we get A B : y − b C D : y + b B C 2 B C = a 2 + 1 a ( x − a ) = a 2 + 1 a ( x + a ) = a 2 + 1 − 2 a 2 + 2 a 2 + 1 = 2 a 2 + 1 2 Since it is a square, then A B 4 a 2 + 2 2 a 2 + 1 a = B C = 2 a 2 + 1 2 = 2 = 2 2 − 1 Hence A B = 4 a 2 + 2 = 4 ⎝ ⎛ 2 2 − 1 ⎠ ⎞ 2 + 2 = 4 8
A nice alternative; using distance between two lines formula instead of using the 4 5 ∘ condition. Thanks for sharing.
Yikes Wait, isnt it the one where it's as close to the corners touching the hyperbolas, so 1.414 is 2 , so our values are 414, and we want the one thats just a tiny bit bigger than one with side 2 , so the value still is 414? Probably my reasoning is going wacko again... :P
That is exactly what I did!
In your case, the sides of the square won't be tangent... There is a reason why this is rated level 5 and not level 2.
well, when i did it, it wasnt level 5
@David Lee – Oops, I forgot that the level can only be seen by me.
Is there a reason why so many people tried it so fast?
 Imgur
Imgur
This problem is pretty hard... did I word the problem incorrectly, or did the people who tried just misread?
Ummm... dude, everybody put 1 0 0 0 as their answer. The diagram is misleading. D:
I added a warning on the problem. Is it OK now?
@Daniel Liu – I think you should have the staff completely take it down. Having it up is misleading, but giving the clue is also too leading towards the right answer.
@Finn Hulse – Finn, even if I blatantly put a diagram of the exact answer up on the problem, the actual task of finding the correct numerical answer to input is still very challenging. It isn't even my fault that the problem solvers were mislead; they evidently did not read the question carefully enough. I see no reason why you would want to take it down completely; doesn't the warning I put on the problem suffice?
@Daniel Liu – No bro! Dude, here's everybody's thought process:
Let's find a square tangent to this hyperbola!
Ooh look, a pretty diagram illustrating exactly what I was looking for!
Hey, I know how to find the side length of this! It's two!
What's this about a warning? Trying to throw me off or something. It's so easy!
What's all this junk about S ? Oh, I get it.
Then S = 1 !
So the answer is 1000!
If I asked you Classic Geometry Problem and put one of @Sreejato Bhattacharya 's crazy diagrams, what do you think would happen? Exactly! :P
@Finn Hulse – I don't think anyone would ignore a warning like that... If they did, it is completely their fault.
@Daniel Liu – Dude, for most people it doesn't make intuitive sense to have a square smaller than that! So they think that you just posted a really easy problem, and you're (quite weakly) trying to throw them off by putting the warning. :O
@Finn Hulse – I don't think I have ever seen a problem where a warning was meant to throw people off...
@Daniel Liu – Yeah, haha. I dunno, that would be my train of though. :D
I overcomplicated this problem so much. I was thinking the only possible way there could be another solution was if it was a hyperbolic square, which actually makes no sense when you think about it. Good solution.
Let the upper right corner of the square be A , the upper left corner be B , and the origin to be O . Clearly, the side length of the square is smallest when the square is tangent to the hyperbola at point A . Let A = ( x , y ) . Clearly, since A is on the top half of the hyperbola, y = x 2 + 1 so A = ( x , x 2 + 1 )
Finding the side length of the square in terms of x
Since the square is rationally symmetric about the origin, the side length of the square is the distance between the points A = ( x , y ) and B = ( − y , x ) . This is simply 1 + S = ( x + y ) 2 + ( x − y ) 2 = 2 x 2 + 2 y 2 = 2 x 2 + 2 ( x 2 + 1 ) = 4 x 2 + 2
So if we find the x-coordinate of point A , we will be able to find the side length of the square using the above formula.
Now, notice that because the continuation of A O is a diagonal of the square, ∠ B A O = 4 5 ∘ . So if we can find the slope of A B and A O , then we can set the degree measure between the two lines to equal 4 5 ∘ .
Finding the slope of A B
Let the point of tangency be ( a , a 2 + 1 ) . The derivative of x 2 + 1 is x 2 + 1 x , so the slope at point ( a , a 2 + 1 ) is a 2 + 1 a .
Finding the slope of A O
Since A O passes through A = ( a , a 2 + 1 ) and O = ( 0 , 0 ) , the slope is simply a a 2 + 1 .
Now that we know the slopes of A B and A O , we can set the degree measure between them to equal 4 5 ∘ : tan − 1 ( a a 2 + 1 ) − tan − 1 ( a 2 + 1 a ) = 4 5 ∘
Taking the tan of both sides: tan ( tan − 1 ( a a 2 + 1 ) − tan − 1 ( a 2 + 1 a ) ) = 1
Using the tangent angle difference property: 1 + ( a a 2 + 1 ) ( a 2 + 1 a ) a a 2 + 1 − a 2 + 1 a = 1
Simplifying: a a 2 + 1 − a 2 + 1 a = 2
Let n = a a 2 + 1 . The equation transforms into the much simpler n − n 1 = 2
Rearranging: n 2 − 2 n − 1 = 0
Using the quadratic equation, we obtain that n = 1 ± 2
Case 1: n = 1 − 2
We substitute back to get a a 2 + 1 = 1 − 2
Simplifying and rearranging: a 2 = 2 − 2 2 1
However, since 2 − 2 2 1 is negative, a is not real. Thus, n = 1 − 2 is an extraneous solution.
Case 2: n = 1 + 2
Doing the same thing as last time, we obtain a 2 = 2 2 − 2 1 a = 2 2 − 2 1 = 2 2 − 1
Finishing up the problem
We plug a = 2 2 − 1 back into the first formula we derived: A B = 4 ⎝ ⎛ 2 2 − 1 ⎠ ⎞ 2 + 2 = 4 ( 2 2 − 1 ) + 2 = 2 2 − 2 + 2 = 2 2 = 4 8
Thus 1 + S = 4 8 ≈ 1 . 6 8 1 , and ⌊ 1 0 0 0 S ⌋ = 6 8 1 .