Smartphone gymnastics
Josh is flipping his phone as he waits for the subway. He finds that he can flip it stably around two of the three axes shown in the diagram. Curiously, when he tries to flip it around the third, he finds that the flip becomes unstable and the phone starts to rotate about the other two axes.
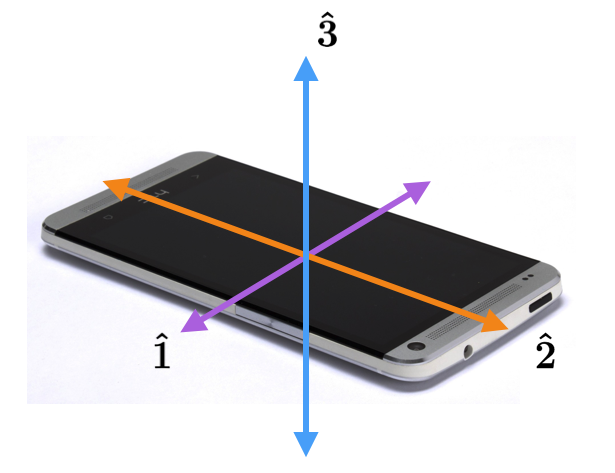
Which is the unstable axis?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Josh, this should be a wiki, instead of just a solution buried in a Level 3 problem. You weren't kidding when you said you'd get back to this one.
Yeah. What he said.
Whoa... Nice write up, @Josh Silverman !
Just try it with your cell phone
Can you think of a less expensive way to do it?
Log in to reply
Yes, just mentally try it with your cell phone.
But this is a really interesting question why.
I must confess, I wouldn't have come to the rigorous derivation myself. I found it here
There is a perturbation analysis in the comments section. You get a 2nd order diff eq that yields either a sinusoid (which is deemed stable) or an exponential (which is deemed unstable), depending on the product of the differences of the moments (which can be positive or negative, depending on their relative values). Although it seems to me that the "omega 3" solution could be a decaying exponential as well as a growing one. Would the decaying exponential not be stable?
Log in to reply
If it doesn't appear in a few days, I'll make sure to go through the argument.
Log in to reply
@Josh Silverman – A less expensive way , go in a cell phone shop ,, ask for one and test its durability.
But what if it's a flip phone ?
Log in to reply
This reminds me of a physics question, which goes, "Can an astronaut in free space somehow turn around and look in a different direction? How would he do it?"
Log in to reply
Sounds like a good one. I won't be mad if you post it.
Log in to reply
@Josh Silverman – I used to be a springboard diver, so that should give you a clue how. Well, I need to find some good pictures.
Now I'm going to have to post a problem on the moment of inertia for a flip phone.
You can see in the diagram the company is htc . It does not manufactre flip phone .lol
...or what about the slider cell phone with keyboards? This is a bit similar to flip phone to me, but I could be wrong.
The instability of a rectangular prism about the axis having intermediate moment of inertia,3 has the largest,2 has the smallest moment of inertia so the intermediate moment of inertia is of the said axis which will wobble on slightest perturbation
We start from the equations of motion for a solid object (I also derive those equations from first principles at the bottom for anyone who is unfamiliar).
The equations of motion are given by
I 1 ω ˙ 1 I 2 ω ˙ 2 I 3 ω ˙ 3 = ( I 2 − I 3 ) ω 2 ω 3 = ( I 3 − I 1 ) ω 1 ω 3 = ( I 1 − I 2 ) ω 1 ω 2 where the ω i are the angular velocities of the phone about its principal axes, and I i are the moments of inertia about those principal axes.
This may look like a complicated set of coupled equations we need to solve, but we can actually figure out what our cell phone is going to do by thinking through the symmetry of these equations. In fact, the essential physics of the problem is captured in the sign of the ( I j − I k ) multipliers out in front. For argument's sake, let's assume that I 1 > I 2 > I 3 , then the signs are + , − , and + , respectively, thus we can analyze
ω ˙ 1 ω ˙ 2 ω ˙ 3 = + ω 2 ω 3 = − ω 3 ω 1 = + ω 1 ω 2
We notice that ω 1 has its extrema when either ω 2 or ω 3 are zero. The same is true for the other two directions.
First, consider the case where we make a slight mistake in our initial flip so that ω 1 = ω ( 0 ) and the other two axes have a small component of the angular velocity ε , with ω ( 0 ) ≫ ε . Initially, ω 1 and ω 3 will both increase, as ω 2 ω 3 and ω 1 ω 2 are both positive. By contrast, ω 2 will decrease, eventually crossing zero at time T 1 . At T 1 , both ω 1 and ω 2 will begin to decrease while ω 3 will start to increase, eventually crossing zero at time T 2 . At T 2 , ω 2 is zero which causes ω 1 to begin to increase and ω 3 to begin to decrease. As we noted above, ω 1 has an extrema for each extrema of ω 2 or ω 3 . Also, as ω ( 0 ) ≫ ϵ , ω 2 and ω 3 cross zero before the value of ω 1 change significantly. Thus, ω 2 and ω 3 oscillate about zero out of phase by π / 2 , while ω 1 oscillates with twice the frequency near ω ( 0 ) .
We see this case plotted below (with the three curves stretched to visualize their oscillatory behavior).
Therefore, flips about the 1 ^ axis are stable. The same analysis holds for the axis of minimal moment of inertia 3 ^ as shown below
Now, consider rotations about the 2 ^ axis so that ω 2 starts at ω ( 0 ) and the other two axes start with angular velocity ε . Initially ω 1 and ω 3 will increase. However, they will continue to increase until ω 2 crosses zero. As energy is conserved, it isn't possible for ω 1 and ω 3 to increase without bound, so ω 2 is quickly pulled down toward the axis. Thus, the rotation about 2 ^ quickly devolves into rotations about 1 ^ and 3 ^ . After some time, those rotations are suppressed and the phone starts again to spin around 2 ^ again, starting the cycle all over again. Interestingly, the oscillations about 2 ^ have half the frequency as those about the other two axes.
Putting this all together, we see that rotations around 1 ^ and 3 ^ are stable to small errors in initial setup of the flip. By contrast, rotations about 2 ^ will vanish as small initial errors blow up into significant rotations about the other axes.
In the case of our cell phone, we have I 3 > I 1 > I 2 so that any attempt to rotate the phone about the 1 ^ axis will transform into rotations about the other, stable axes of rotation.
Appendix
We are interested in the rotation of the phone around its intrinsic axes 1 ^ , 2 ^ , and 3 ^ . To change the angular momentum of the phone about some axis requires a torque about that axis. But what are the torques on the phone in a uniform gravitational field? About the center of mass, there are no torques on the phone, i.e. τ = 0 , and thus d t d L = 0 . This means that the total time derivative of L in the frame of the room has to be zero. We can use this fact to find how the phone's rotation progresses.
We start by formulating the total angular momentum of the phone. From 2-dimensional rotations, we're familiar with the idea that L = m R v , where R is the distance of the particle from the axis of rotation and v is a particle's tangential velocity. When there are multiple axes of rotation about which the phone may spin, we need to consider them all.
First, we need to express velocity in terms of ω and r . Let's consider a particle performing counterclockwise rotation about the z -axis, so that ω points upward. We are free to calculate v when it is most convenient, so consider the moment when r lies along the positive x -axis and v points in the negative y -direction. The velocity vector v is perpendicular to both the position and the angular velocity vectors, and is a product of them both, so we expect v to be the result of a cross product between them. Should we use v × ω or ω × r ? Let's calculate to find out:
v = det ⎝ ⎛ x ^ r x ω x y ^ r y ω y z ^ r z ω z . ⎠ ⎞
In our case, only r x and ω z are non-zero, thus we have v = + ω z r x = + ω r . We know from the one dimensional definition that it is actually − r ω , thus we must have ordered them incorrectly in the product. This shows that v ≡ ω × r .
By a similar use of test cases, and the fact that L is perpendicular to r and ω , we can show that the angular momentum of a particle is given by L = r × ω = r × ( ω × r ) .
Now, we're not just considering the angular momentum of a particle, but of a solid object. This means we must integrate over all the point particles that constitute it: L = ∫ δ m r × ( ω × r ) .
Here it is very important to be clear about what frame we're calculating in. The axes we use are defined with respect to the phone, i.e. no matter how the phone is rotating, the axis 2 ^ will always be oriented lengthwise along the phone, and through its center of mass. So, even if the phone spins along the other axis, causing 2 ^ to rotate in space, we can still plainly express the rotations about it. Note that this means the axes 1 ^ , 2 ^ , and 3 ^ are rotating with respect to the inertial frame of the room. Note this also means that the moment of inertia of the phone about any of its intrinsic axes is constant. Take a moment to think about this.
Returning to the calculation, we can find the change in L by taking the time derivative. Dropping the integration for ease of writing, we have L ˙ = r ˙ × ( ω × r ) + r × ( ω ˙ × r ) + r × ( ω × r ˙ ) = ( ω × r ) × ( ω × r ) + r × ( ω ˙ × r ) + r × ( ω × ( ω ˙ × r ) )
with the first term vanishing because A × A = 0 for any vector A .
The third term is a bit hairy with three cross products appearing. We can simplify this using the vector identity a × ( b × c ) = b ( a ⋅ c ) − c ( a ⋅ b ) . Applying this to the third term, we get r × ( ω × ( ω × r ) ) = ω ( ω ⋅ ω × r ) − ω × r ( r ⋅ ω ) . The first term vanishes since ω is perpendicular to ω × r .
At last we have the result we seek L ˙ = r × ( ω ˙ × r ) − ω × r ( r ⋅ ω ) . Now, as L ˙ = 0 , this relation becomes r × ( ω ˙ × r ) = ω × r ( r ⋅ ω ) .
Let's write this out in terms of components to see what it is saying. Taking for instance the 1 ^ component, we find for the left hand side r × ( ω ˙ × r ) 1 = ω 1 ( r 2 2 + r 3 2 ) which is just the angular momentum about the 1 ^ axis times the sum of the squared distances from the 1 ^ axis. We recognize this as I 1 ω 1 .
On the right side, things are a little simpler and we have ( ω × r ) 1 ( r 1 ω 1 + r 2 ω 2 + r 3 ω 3 ) = ( ω 3 r 2 − ω 2 r 3 ) ( r 1 ω 1 + r 2 ω 2 + r 3 ω 3 ) = r 1 r 2 ω 1 ω 3 + r 2 2 ω 2 ω 3 + r 2 r 3 ω 2 ω 3 − r 1 r 3 ω 1 ω 2 − r 2 r 3 ω 2 2 − r 3 2 ω 2 ω 3 .
Summing over all the mass elements in the phone, the cross terms (i.e. r 1 r 2 ) vanish, leaving us with the terms like r 1 2 so that we have ( r 2 2 − r 3 2 ) ω 2 ω 3 which is equal to ( I 2 − I 3 ) ω 2 ω 3 .
Thus, after all that we're left with a simple expression for the change in ω 1 : I 1 ω ˙ 1 = ( I 2 − I 3 ) ω 2 ω 3 .
By symmetry, we can immediately write down the equations for the other two axes: I 2 ω ˙ 2 I 3 ω ˙ 3 = ( I 3 − I 1 ) ω 1 ω 3 = ( I 1 − I 2 ) ω 1 ω 2