Flowery Union
In a club of 40 executives (all of whom like flowers), 33 like Red Roses and 20 like Black Roses. How many like both?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Wonderful! I liked what you've done here especially with the text colors in the diagram. Keep it up!
Wow, the question has been changed from cigarettes to flowers. More kid-friendly, I guess.
Now, let the number of executives who like both be x .
The number of executives who like Red Roses only = 3 3 − x
The number of executives who like Black Roses only = 2 0 − x
The number of executives who do not like flowers = 0
These four numbers add up to 4 0 :
x + ( 3 3 − x ) + ( 2 0 − x ) + 0 = 4 0 5 3 − x = 4 0 x = 5 3 − 4 0 = 1 3
You can use a Venn diagram to illustrate this. Try it yourself!
Yes, ofcourse flowers are more kid friendly. Nice algebraic approach. And yes venn diagrams would be nice so I added a solution. (+1)
(33-x)+(20-x)+x=40 thus x=13
You should say that N o b o d y d o e s n ′ t l i k e a n y o f i t
Log in to reply
Thanks @Pham Khanh for the nice suggestion. It has been updated. :)
Can you make your solution more detailed so that others can understand it? Thanks :)
BTW, nice problem.
Log in to reply
the value of x is equal to 13 50+13=63 63-40=13
Log in to reply
You haven't mentioned what x represents. And how is x equal to those values?
Log in to reply
@Sandeep Bhardwaj – let the x be the number of executives who like both...slow learner..haha
Log in to reply
@Lorenz Navales – haha. thanks for explaining this. Could you please update this in your solution?
Log in to reply
@Sandeep Bhardwaj – of course haha. by the way nice suggestion thank you very much...
@Sandeep Bhardwaj – Naughty staff XD
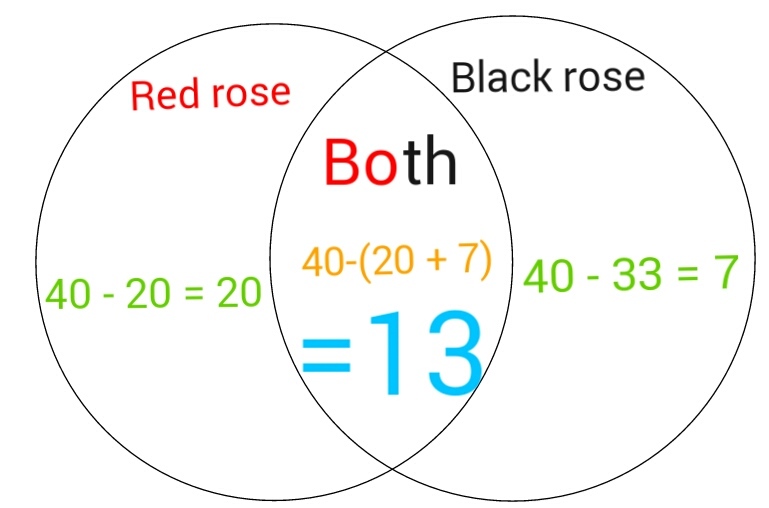
Lets draw a venn diagram and evaluate. The number of people who like red roses only = total number of people - people liking black roses = ( 4 0 − 2 0 = 2 0 ) and thise liking black roses only = total people - people liking red roses = ( 4 0 − 3 3 = 7 ) . So those who love both = 4 0 − ( 2 0 + 7 ) = 1 3 . Everyone loves a flower so the universal set does not contain those who love neither the flowers.