Dice stacking

Logic Level 2

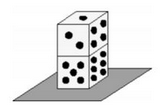Two ordinary six-sided dice are stacked on top of each other and placed on a table top as shown above. What is the sum of the dots on all the visible faces?

The answer is 29.

4 solutions

Aditya Ketkar
Nov 10, 2014

It's pretty straight forward.............

" The sum of two numbers on opposite faces of a dice is always 7 "

(of course for a 6 sided dice)

When stacked there are always three faces covered. Therefore it matters which face is up/on top. The answer can change... This was poorly thought out.

chris Robertson - 6 years, 7 months ago

the question asks on the image shown. so we should base it on the image i say

Kim Ian Macay - 5 years, 6 months ago

According to image the answer will be 18 but it is not that

Aman Verma - 5 years, 5 months ago

@Aman Verma – we have to infer that the visible faces of the dice are the one's that are covered by stacking a die on top of another and a die on top of the table or whatever surface that is. well i see your point though.

Kim Ian Macay - 5 years, 5 months ago

Actually for the visible side faces, you can apply that logic ie the sum of numbers on opposite faces is 7 so you get 28... Add the remaining number, in this case 1, to it. That way here you get 29

Aadi Naik - 6 years, 7 months ago

Haha, yes you are correct. My response doesn't indicate the logic I am using: The rule above needs to have opposing pairs of faces in order to work (meaning an equal number of exposed faces). In the case of two stacked dice resting on a surface, there are always three faces covered leaving an unpaired face which is entirely random and allows for the answer to change (between 29 and 34). My issue is that the problem doesn't state that the given image is the specific answer it wants, (I was overthinking a simple problem in other words) and was indicating the ambiguous wording was at fault.

chris Robertson - 6 years, 7 months ago

@Chris Robertson – Actually at first I thought the same thing that the problem did not indicate the diagram was to be followed... Then I realised that there can be one answer so I wrote 29...

Aadi Naik - 6 years, 7 months ago

@Aadi Naik – Aadi, did you get 29 without following the diagram? My answer is also 29 but if i follow the diagram otherwise i think you can not solve the problem.

Punit Bansal - 6 years, 7 months ago

@Punit Bansal – Following the diagram I get 29. Doing it assuming that the dice are arranged randomly I get range answer 29-34 like Chris got

Aadi Naik - 6 years, 7 months ago

@Aadi Naik – Why would you not assume the diagram was part of the question?

Tom Franclemont - 6 years, 1 month ago

My say exactly.

Daniel Arenson - 6 years, 7 months ago

Why only '7'???

Aparna Kalbande - 5 years, 6 months ago

It sucks that you have to know the rule about the sum of opposite faces, you would assume that the problem is solvable otherwise with pure logic.

Max Merco - 4 years, 7 months ago

I think that the logic is correct, the part where the one needs to be added should easily be thought out and it was a very simple question altogether.

Akshayan Manivannan - 4 years, 6 months ago

Saurabh Sharma
Nov 12, 2014

sum of number son opposite faces is equal to 7 so 4 pairs are visible and 1 extra face showing number 1 on the top is visible.... so 7x4 +1 = 29

Ricky Wahyudi
Nov 12, 2014

Sum of numbers (number of dots) on two opposite sides of ordinary die is always 7. On the top die of the picture, we know that if the top side is 1, the hidden opposite side will be 6. And the bottom die has 2 opposite sides that not visible, so the sum the hidden two sides is 7. The total hidden dots are $6+7=13$ Every single die has $1+2+3+4+5+6=21$ dots., so if all faces are visible, we have 42 dots. We know that Sum of the dots on all visible faces = $42-13=29$

Agree with Rickhy

Usman Banka - 6 years, 7 months ago

Congratulations

Aruna Chauhan - 4 years, 5 months ago

Anna Anant
Nov 13, 2014

29, in a die.. the sum of opposite faces should be 7. so its 4 x 7 + 1 (on top) = 29.

Dice stacking

The answer is 29.

4 solutions

0 pending reports