I'm on Psychedelic

Let the radius of the circle be ' $a$ '.

Outermost Brown Area

$= 4 \times$ (Area of Brown Segment in the corner) + $8 \times$ (Area of the Smaller Brown Segment)

$= 4 \times A + 8 \times B$

Where,

$A = a^2 - \pi \frac{a^2}{4}$

To get area of $B$ , draw a square of side $a$ joining the top left and top middle circle's centers and the points where topmost line touches there two circles.

This area can be seen as consisting of region B, two sectors each of $\angle 30^\circ$ , and an equilateral triangle of side $a$ :

$B = a^2 - 2 \times \pi \frac{a^2}{12} - \frac{\sqrt{3}}{4} a^2$

Solving it for $a = 4$ , we get

Brown Area $= 4 \times A + 8 \times B = 19.28824$

All of your solution is so simple...I used integral. Anyways here: 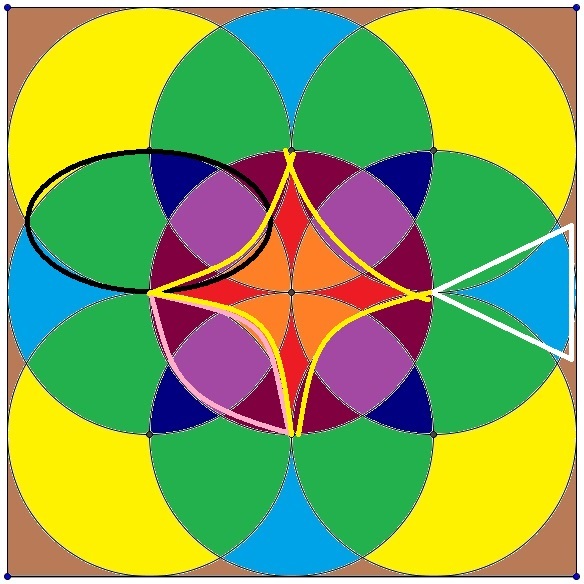Yellow outline=Y Pink outline=P Black outline=B White outline=W The inside is $4*4^{2}π+4W+Y$

W is the same as $(16π-2*B)/2$ .Now B can be expressed as an integral by using the circle equation. Which is 4\int_0^\sqrt{12} \sqrt{16-x^2}-2 \mathrm{d}x . Therefore, W= (16π-8\int_0^\sqrt{12} \sqrt{16-x^2}-2 \mathrm{d}x)/2

Y is essentially $16π-4P$ = 16π-16\int_0^\sqrt{8} \sqrt{16-x^2}-2\sqrt{2} \mathrm{d}x

$2\sqrt{2}$ because it forms a 45-45-90 triangle with 4=r as hypotenuse.

This yields 236.712. Subtracting from total area $16^{2}$ , it's 19.288

very simple if you break the image down into parts.

the area of the smaller brown regions=

= 8 (16- ((sqrt3/4 (4^2))+(2 (30/360 pi 4^2))) + 4 (16-((pi*4^2)/4))

= 19.288

Find the area of the corner brown areas by subtracting the 16 pi circle area from the 8x8 tangential square around that circle. So 64 - (16 pi)= 13.734517542. Keep this as the area of the 4 brown corners of the large square. Use the area of a vesica picis lens to find the area of the overlap forming the smaller brown areas on the edge. The leftover from two vesica picis lenses ( about 1.2284 r^2 per lens) subtracted from the 16 pi circle area is divided in 4 to get the area to subtract from one of those brown corner areas. So one brown corner area is 13.734517542 divided by 4, or 3.436275. The leftover from subtracting the 2 lenses is divided in 4 to get the amount to subtract from this brown corner area, so 3.436275 minus 2.739170614 equals 0.6971044, multiplied by 8 equals 5.57683, which is added to the 4 corner areas, 13.734517542 plus 5.57683 equals 19.311 using truncated calculator amounts, but with full precision it comes close enough so I passed for the given answer of 19.288.

Area of Brown Region $=$ Area of Large Square $-$ Area of Small Square $-4$ ( $\frac{3}{4}$ Area of Circle) $- 4$ (Area of Blue Region) The small square is the square formed by the centers of the four yellow circles. Because we subtract this squares's area, we only subtract 3/4 the area of each of the yellow circles. We get twice the area of the blue region if we subtract two times the area of the green, navy, pink, and maroon regions from that of the circle.

I was about going to be crazy yesterday after inputting the correct answer but it showed that I got the wrong answer.. :3