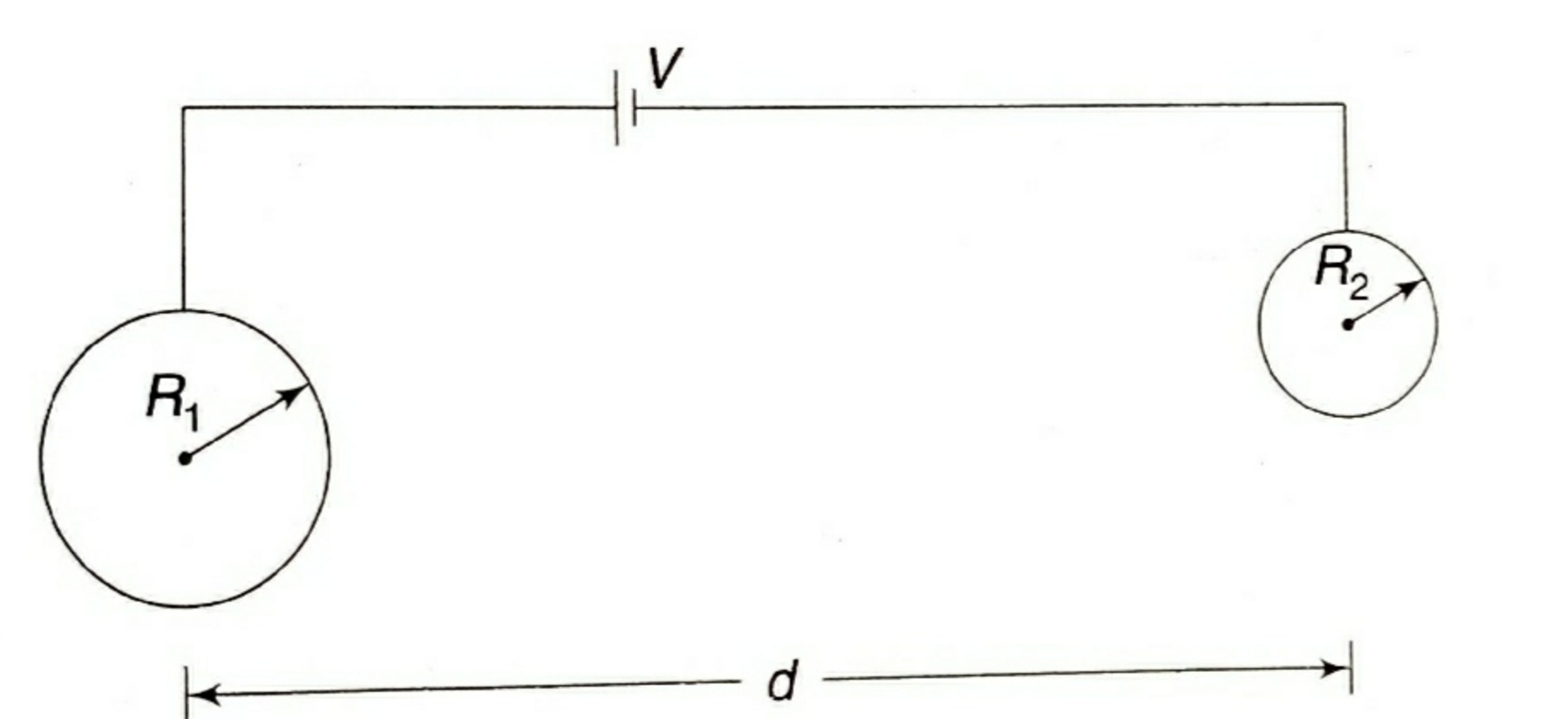
Solid Conducting Spheres
Two solid conducting spheres of radius
R
1
and
R
2
are kept at a distance
d
(
>
>
R
1
and
R
2
)
apart.
The two spheres are connected by a thin conducting wires to the positive and negative terminals of a battery of emf
V
.
Find the electrostatic force between two spheres. Type your answer by multiplying
1
0
4
with your answer.
Details and Assumptions
1)
R
1
=
2
2)
R
2
=
1
3)
V
=
1
0
4)
d
=
4
0
0
5)
ϵ
0
=
1
The problem is taken from my Physics book.
The answer is 34.906.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Karan Chatrath
Hii
I have edited the problem , which you reported
By the way I have some doubts, are you free?
Log in to reply
You have requested a clarification from Mr Chase, so I look forward to hearing his take on it. I may be wrong and that is okay.
I am attempting the torque problem right now after which I will be away for some time. I can try answering your questions but do post an attempt, or describe your approach. I would really appreciate that, then I can probably help better.
Log in to reply
@Karan Chatrath
Asking to Steven chase for clarification
Did it hurt you? Sorry.
I was just asking him to check. Because he uses python.
Log in to reply
@Talulah Riley – No, not at all, don't worry.
@Talulah Riley – I have shared my attempt in the report, so you can tell me my mistake if you see it.
Log in to reply
@Karan Chatrath – @Karan Chatrath off course . In the meantime upload the solution of magnetism and torque. Bye
@Karan Chatrath and I am expecting a analytical solution from you of the problem Magnetism and Torque.
An important thing to note is that due to conservation of charge, the charge leaving one sphere will be equal to the charge accumulating on the other. The surface potentials are then:
V 1 = R 1 k q V 2 = − R 2 k q
The difference between the surface potentials is equal to the battery voltage:
V 1 − V 2 = R 1 k q + R 2 k q = V
Solve for q . Then the force between the spheres is:
F = d k q 2 ≈ 1 0 0 0 0 3 4 . 9
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
|
@Steven Chase I didn't understand why the potential difference is equal to battery voltage??
Log in to reply
The battery is connected between the surfaces. So the difference between surface potentials is equal to the battery voltage
@Steven Chase
Check the latest problem. Because the karan sir has already reported it.
I don't think, there is anything wrong in probelm.
Log in to reply
I'll take a look, but it will be a while from now, since I'm going to bed and I have to work tomorrow
Log in to reply
@Steven Chase
No problem. Goodnight
By the way what work you do?
@Steven Chase sir can you provide me a python code for this problem
Log in to reply
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
|
Log in to reply
@Steven Chase oh sorry, I was attaching a problem from my gallery, but instead of that another thing I have uploaded above. I am editing it right now.
@Steven Chase
The comment is edited now, and by the way Thanks for this code also.
It is like one arrow and two targets
Code only really helps if you want a time-domain simulation. You can calculate the steady state charge easily without code. Voltages are in red, and current arrows are in green. The sum of the three green currents is the capacitor current, which must be zero in steady state.
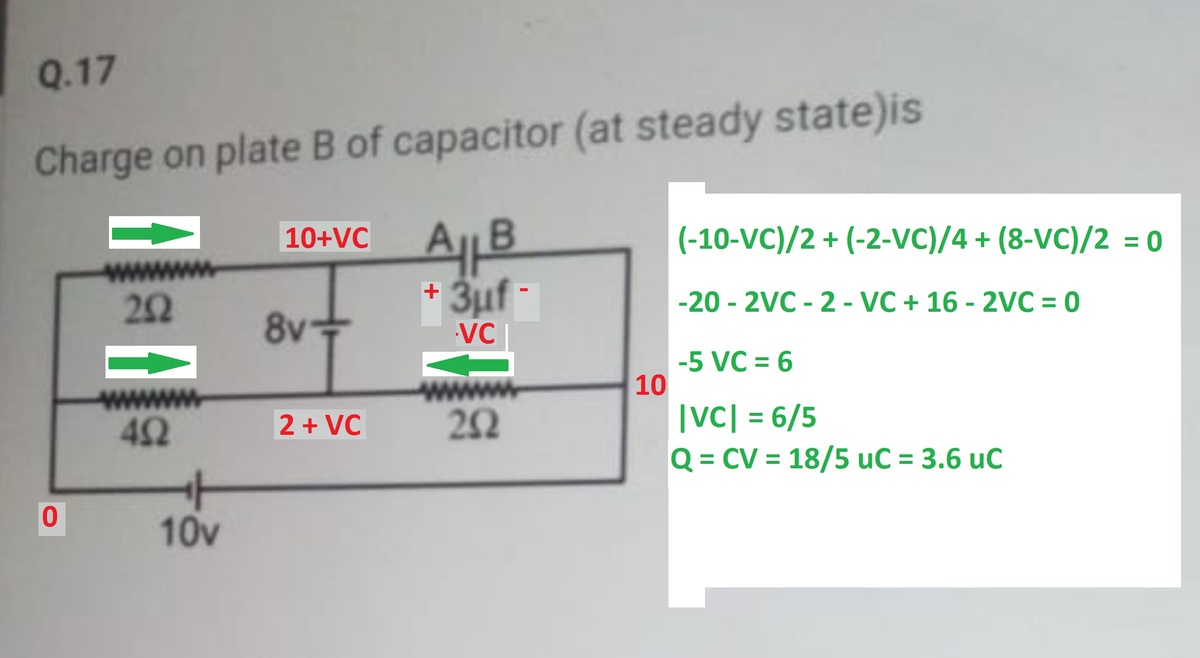
Log in to reply
@Steven Chase in this way I solved it orally. I just want CODE .
Log in to reply
@Talulah Riley – What will code do for you here?
Log in to reply
@Steven Chase – @Steven Chase the code will find charge as function of time and then we will program it to put t = ∞
@Steven Chase I have little bit doubt with my today's magnetism problem. Can you post its solution?
@Steven Chase can you post a analytical solution of this Problem
Log in to reply
I solved it numerically. I'm sure someone will post an analytical solution
Log in to reply
@Steven Chase No problem post a numerical solution. It is also helpful for me. Thanks in advance.
@Steven Chase
I am getting 0 but it is not accepting, and i don't think I have right to report you problem.
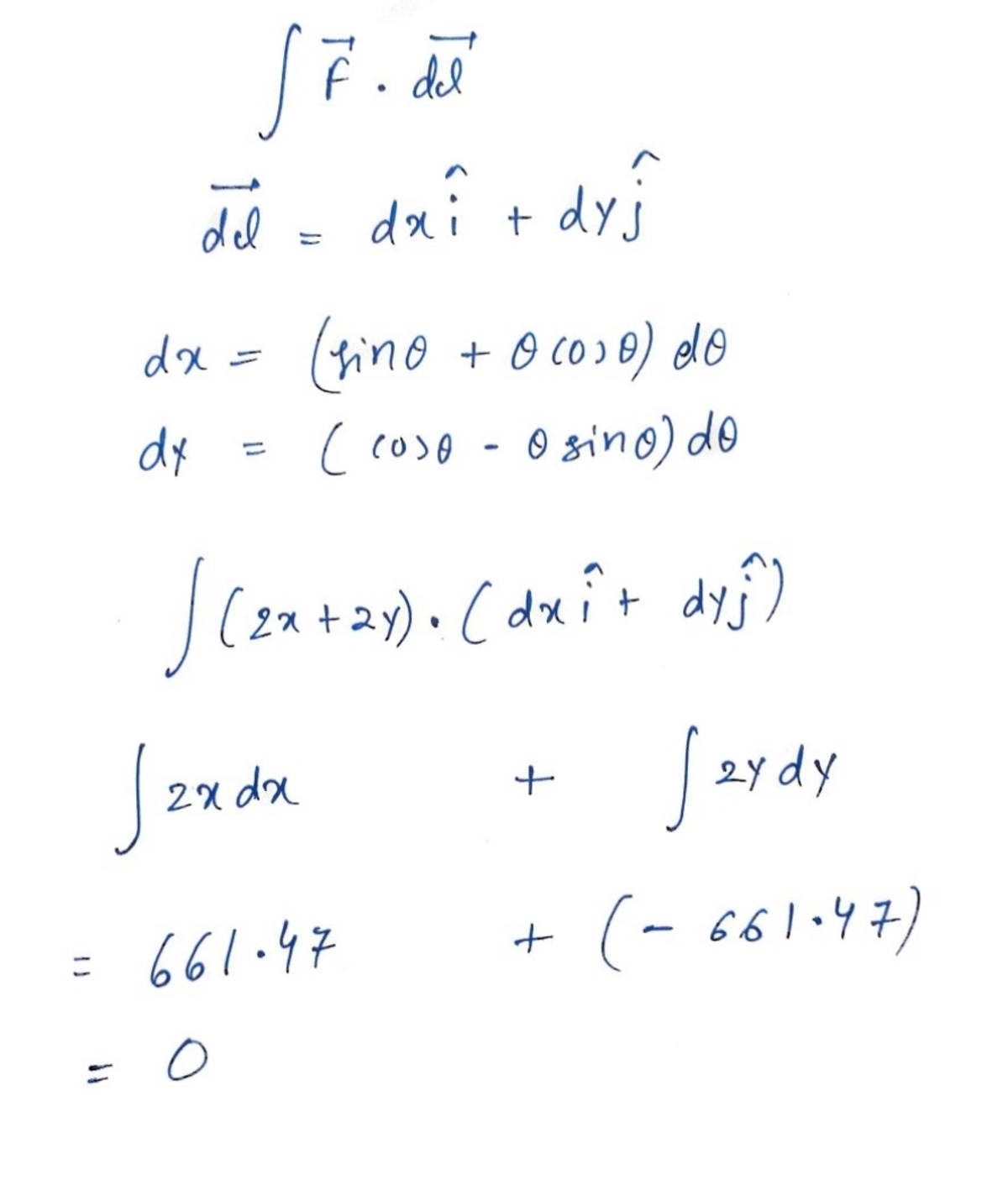
Please correct me where I am wrong.
Log in to reply
Double-check your d x and d y expressions. And then compute the integral with respect to θ
The battery can be thought of as a pump of charge that transfers a certain amount of charge from sphere 2 to sphere 1. Let this amount be Q . A negative charge ( − Q ) is induced in sphere 2 while a positive charge( Q ) is induced in sphere 1. Moreover, Since the spheres are connected by a battery, the potential difference between sphere 1 and sphere 2 must be V .
⟹ 4 π ϵ o R 1 Q = − 4 π ϵ o R 2 Q + V
This gives the expression for Q in terms of the other variables. Finally, the magnitude of the force between the spheres is:
F = 4 π ϵ o d 2 Q 2
Evaluating all expressions gives the required answer: 1 0 4 F = 3 4 . 9 0 6 .