Solve for trajectory again

I will first prove that the trajectory will be of an ellipse:

$1$ Considering the motion along X:

since mass is $1$ , the falue of $F=\frac{d^{2}x}{dx^{2}}$

note that $\frac{d^{2}x}{dx^{2}}=v\frac{dv}{dx}$

now: $v\frac{dv}{dx}=-x$

thus, by simple integration, we get $\frac{v^{2}}{2}+\frac{x^{2}}{2}=c_1$

now, at $t=0;v=0;x=1$ so, putting values and calculating, we get $c_1=\frac{1}{2}$

so, the equation can be re-written as:

$v=\sqrt{1-x^{2}}$

and by re-arranging and putting integrals:

$\int{\frac{dx}{\sqrt{1-x^{2}}}}=\int{dt}$

A gen solution of this is $x=sin(t+c_2)$ (for proof of this look at the end)

Now, at $t=0,x=1$ ..Giving $c_2=\frac{\pi}{2}$

so, we get the gen equation for $x=cost$

$2$ Considering Y-axis

note that acceleration and displacement will have the same type of relation like X.

solve them the same way to get:

$v^{2}=2c_3 -y^{2}$

at $t=0,v=2,y=0$

Solve and simplify to get:

$\int{\frac{dy}{\sqrt{4-y^{2}}}}=\int{dt}$

again, a general solution to this is

$y=2sin(t+c_4)$

again, at $t =0,y=0$ giving $c_4=0$

Thus, gen equation for Y:

$y=2sint$

$3$ The Ellipse Part:

the parametric equation of an ellipse is : $(a\cos\theta,b\sin\theta)$ where eccentricity $=e=\sqrt{1-\frac{a^{2}}{b^{2}}}$

in this case, $a=1,b=2$

put values to get $e=\frac{\sqrt{3}}{2}$

Thus, our answer: $\boxed{6}$

proof of $\int{\frac{dx}{\sqrt{a^{2}-x^{2}}}}=\int{dt}$ gives $x=asin(t+k)$ where k is the constant of integration

Let $y=sin^{-1}(\frac{x}{a})$

or, $\frac{x}{a}=siny$

differentiating w.r.t $x$ and re-arranging, we get:

$\frac{dy}{dx}=\frac{1}{acosy}=\frac{1}{\sqrt{a^{2}-a^{2}sin^{2}y}}$

putting values of $siny$ and simplifying, we get:

$dy=\frac{dx}{\sqrt{a^{2}-x^{2}}}$

therefore, $\int{\frac{dx}{\sqrt{a^{2}-x^{2}}}}=\int{dy}=y=sin^{-1}(\frac{x}{a})$

the rest is followed

The resulting motion can be thought of as two separate simple harmonic motions one along each axis because of the given form for the force. First consider a motion along X-axis. The maximum amplitude along this axis is $b = r_{0}$ because at that point the component of velocity along x-axis is zero. To calculate the amplitude of motion along Y-axis, let us use energy conservation. The kinetic energy for $y=0$ is $\frac{1}{2}mv_{0}^{2}$ . The potential energy when particle is at the extreme point on Y-axis (say $y=a$ ) is $\frac{a^{2}}{2}$ . Hence we have, $b^{2}=mv_{0}^{2}$ Thus, the eccentricity of the ellipse is given by: $e = \sqrt{1-\frac{a^{2}}{b^{2}}}=\sqrt{1-\frac{r_{0}^{2}}{mv_{0}^{2}}}$ Substituting the given values, we get, $\boxed{e=\frac{\sqrt{3}}{2}}$

Interestingly, this forms a sort of attracting field, with the the force field pulling the object towards the plane's centre.

This forms a symmetric ellipse, about the y and x-axes. Here's an image I made by simulating the trajectory:

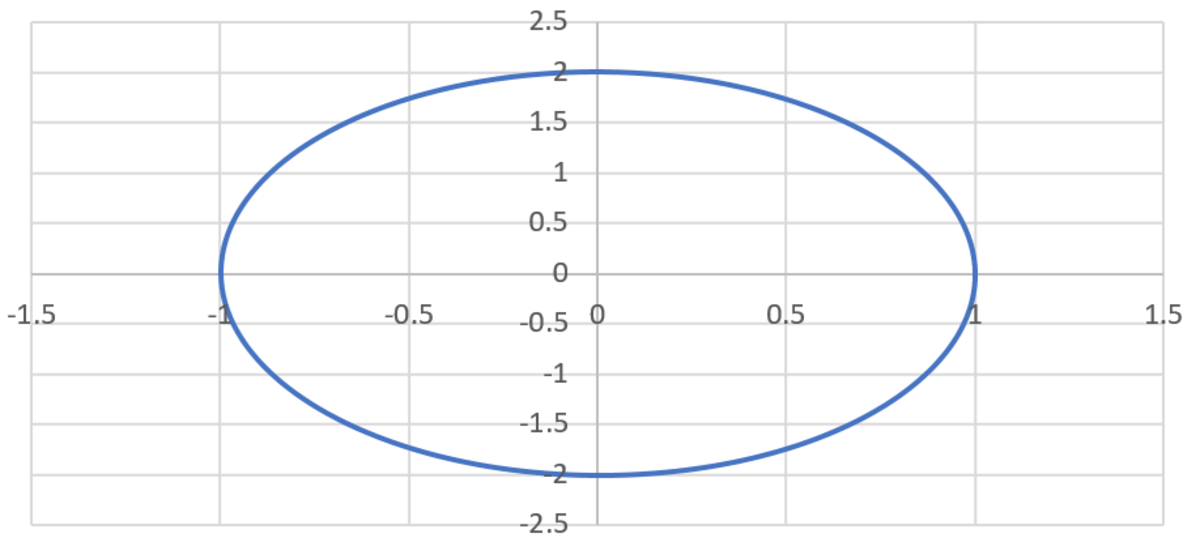
Here is the simulation:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

import math

time = 0 #initial time              
deltaT = 10**-2 #timestep

r  = [1,0] #initial position vector
rDot = [0,2] #initial velocity vector   

Rx = [] #x values   
Ry = [] #y values

while time <=6.5: #simulating to 2.5 seconds
    Rx.append(r[0]) 
    Ry.append(r[1])

    rDotDot = [-1*r[0], -1*r[1]] #Force field calculation 

    rDot[0] = rDot[0] + rDotDot[0]*deltaT #numerically integrating to get x velocity
    rDot[1] = rDot[1] + rDotDot[1]*deltaT #numerically integrating to get y velocity

    r[0] = r[0] + rDot[0]*deltaT #numerically integrating xdot to get x position
    r[1] = r[1] + rDot[1]*deltaT #numerically integrating ydot to get y position

    time = time + deltaT #updating value of time


print("x values: ")

print("")

for i in Rx:
    print(i)

print("")

print("y values: ")

print("")

for j in Ry:
    print(j)

first we know that $dl/dt=r*F$ when force is along the r. net torque about that point is zero.

this implies angular momentum is conserved * $mv*r=constant$ *

let the path followed be * \frac{x^(2)}{a^(2)}\+\frac{y^(2)}{b^(2)}\=1 *

so we look at 2 position

x=a(2(initial velocity),a(magnitude of position vector))

and x=0(v,b)

$vb=2$

now we find radius of curvature at x=0

we found it to be R= \(\frac{a^(2)}{b} )

* $\frac{mv^(2)}{R}$ =b*

hence $b=2$