Solve for trajectory (if you can)
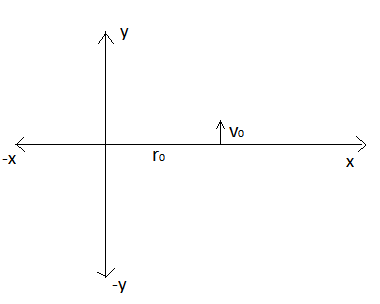 We have placed a particle of mass
m
at
r
→
=
r
0
i
^
.
We have placed a particle of mass
m
at
r
→
=
r
0
i
^
.
At t = 0 we have given it a velocity of v = v 0 j ^ .In the whole co-ordinate plane the force is given by F = r 3 − 8 r N
The title says solve for trajectory but I am telling you that the trajectory of the particle is ellipse.If the eccentricity of the ellipse is given by e = b a where a , b are co-prime integers then find a × b
Details and Assumptions :
1) v 0 = 1 m / s , r 0 = 2 m e t r e , m = 1 K g
2)There are no other force acting on the particle except the force given.
3) Ignore gravity
Also try Solve for trajectory again .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Question is undoubtedly masterpiece One more method of doing this: 1). The Force field is conservative since its divergence is 0.(solenoidal) 2) Since the force magnitude follows inverse square law Kepler's second law (constancy of aerial velocity which is essentially conservation of angular momentum) is applicable 3) Force is directed toward origin therefore origin is one foci of ellipse And x0 =a + ae (here a=semi major axis and e =eccentricity) &, x1=a - ae (x1=other end of major axis) Having said that Since F=8/r^{2} U = -ʃ F.dr (limits r to ∞) Therefore U = -8/r Now applying Kepler’s law at end points on major axis v0ro=v1r1 (v0=1, r0=2) (v0and v1 perpendicular to major axis) v1=2/r1 Now conservation of energy at these two points U0+KE0 = U1+KE1 -8/r0 +m(v0^{2})/2 = -8/r1 +m(v1^{2})/2 = -8/2 + (1×1^{2}/2) = -8/r1 + (1×v1{2}/2) = -4+.5 = -8/r1 +0.5×v1^{2} Putting v1=2/r1 = -3.5 = -8/r1 +0.5× (2/r1)^{2} = -3.5 = -8/r1 +2/r1^{2} = 3.5r1^{2} -8r1 + 2=0 The solution to this eqn. is r=2(as expected) or r=2/7 Now x0=r0 & x1=r1 Or a +ae =2 a-ae=2/7 Solving we get e = 3/4
Log in to reply
Why I posted that kind of solution is because I also wanted to prove that the equation of trajectory is an ellipse.
Nice solution
Wow! Amazing problem and an amazing solution! Thumbs up!
Man, I have a one-line solution to this... Anyways, Lengthy but awesome solution.
Log in to reply
Please post it then
Log in to reply
I cannot...Not a bit comfortable with LATEX
Log in to reply
@Tushar Gopalka – You can use daum equation editor app.I always use this for typing out in latex
Log in to reply
@Ronak Agarwal – I will upload it as soon as I can.....Meanwhile..Please post more awesome Mechanics questions
Log in to reply
@Tushar Gopalka – You can try my new question Groovy Groove
Also, from where did you find the polar equation of ellipse?
How did you integrate?
Ronak Agarwal, I have reffered to books related to this and even derived the differential equation, and a particle does not move in an ellipse when it comes to central cubic forces, instead it is a bunch of asymptotic curves, consider this :
r 3 8 − m ω 2 r = m r ¨ Now ω = L / m r 2 thus :
θ ˙ = m r 2 L hence
d θ = m r 2 L d t
So r ˙ = d θ d r m r 2 L
now put r=1/u then :
r ˙ = d θ d r m L u 2 = − m L d θ d u
Differentiating with respect to time again and using the relation between d θ and d t
We get r ¨ = − m 2 L 2 u 2 d θ 2 d 2 u
Hence substituting into the force equation we get :
r 3 8 − m r 3 L 2 = m r ¨ = − m m 2 L 2 u 2 d θ 2 d 2 u
as r = 1 / u we get the result :
u = m L 2 − 8 m L 2 u ¨
(note here the second derivative with respect to θ whose solution is an SHM
Since in this case the RHS is − v e which means u = A c o s ( x ) a n d r = 1 / A c o s ( x ) which is not an ellipse.
Note-Don't say that I didnt take vector sign of r, it doesnt matter as I considered the purely scalar quantity dsitance from centre.
Log in to reply
I will say that you should consider the vector sign of r . If you have read about newton's laws of gravitation you will find the formula is always given in the form F → = r 3 − G m 1 m 2 r → .
I can't help in this.
Log in to reply
No i agree to that,, i am not saying that,, you see i have derived the equation for the change of distance from the focus,, which is the basis for polar co-ordinates,, infact i can show you it works perfectly for inverse square forces,, see this
(listen,, basically i am only considering the action of forces directed along the radius vector from focus)
http://galileo.phys.virginia.edu/classes/152.mf1i.spring02/KeplersLaws.htm
check this,, dont be too quick to dispose my equations off bro :P i didnt use vector signs because i have already presumed that i am dealing only with those directed along the radius vector,,, not that i am dumb enough to not know that forces are vectors,,, please check the website :)
infact had i taken vector notation,, i should have not included mw^2r as then it would have already been included bia r vector :)
Log in to reply
@Mvs Saketh – I just want to say that I have not given a central cubic force , instead I have given an inverse square force. So all your equations have no meaning.
really a great question, i enjoyed doing it..
Log in to reply
Thanks. You can try my other questions too. By the way can you please share your solution with us
amazing! this was awesome
hello Ronak Agrawal i have a doubt: i didn't understand how did you write -8/r in the place of potential energy i used integration of U=-F.dr and was confused about what to do with the r vector i would be grateful to you if you explain it to me:)
Clearly, the potential energy at a point is r − 8
Let p and q be the major and minor axes , then clearly,
p ( 1 + e ) = r 0 = 2
Also, let r = p ( 1 − e ) be the other extreme end of the ellipse, and v be the velocity at that point.
Then by conservation of angular momentum,
v r = v 0 r 0 ⇒ v = r v 0 r 0
Also, by conservation of mechanical energy,
2 1 m v 2 − 8 / r = 2 1 m v 0 2 − 8 / r 0
Substitute the values of m , v 0 , r 0 and solve to get r = 7 2
Clearly, p ( 1 + e ) = 2 , and p ( 1 − e ) = 7 2
Solve to get e = 4 3
Explain p(1+e)=2...plz
Preamble: in cartesian coordinates ( O , x , y ) :
r = x ı ^ + y ȷ ^ ;
in polar coordinates ( O , r , θ ) :
r = r e r ^ , e r ^ = cos θ ı ^ + sin θ ȷ ^ , e θ ^ = d θ d e r ^ = − sin θ ı ^ + cos θ ȷ ^
The system is conservative, the potential energy by the central force, with V ( ∞ ) = 0 :
F = − r 2 8 e r ^ , is: V = − r 8
so there are two constant of the motion, the total mechanical energy and the angular momentum:
E = 2 1 m v 2 − r 8 = 2 1 m v 0 2 − r 0 8 = E 0
L = m v × r = L 0
the cinematic values in polar coordinates are in this case:
v r = r ˙ , v θ = r θ ˙ , a r = r ¨ − r θ ˙ 2 , a θ = r θ ¨ + 2 r ˙ θ ˙ = 0
so:
L = m r 2 θ ˙ k ^ , L = m r 2 θ ˙ = m r 0 v 0 = L 0 ,
and it can be writed after some algebraic tricks:
v 2 = v r 2 + v θ 2 = ( m L 0 ) 2 ( ( d θ d r 1 ) 2 + r 2 1 )
a θ = 0 , a r = − ( m r L 0 ) 2 ( d θ 2 d 2 r 1 + r 1 )
we can write the simple equation of motion;
a r = − r 2 8 ,
( d θ 2 d 2 r 1 + r 1 ) = L 0 2 8 m 2
but now i choose the method that use the conservation of the constant of the motion E 0 , L 0 , thus:
E 0 = 2 1 m ( m L 0 ) 2 ( ( d θ d r 1 ) 2 + r 2 1 ) − r 8
that can be rewrited:
d θ = r 2 L 2 2 m ( E 0 + r 8 ) − r 2 1 d r
d θ = 2 m L 0 r 2 E 0 + r 8 − ( 2 m L 0 ) 2 r 2 1 d r
changing the variable r in:
u − u 0 = r 2 m L 0 so that in the square root there will be a difference of squares:
( a + u ) ( a − u ) = ( a 2 − u 2 ) which implies:
u 0 = − L 0 2 m 8 m , a 2 = E 0 + L 2 3 2 m we obtain:
d θ = − 1 − ( u / a ) 2 d ( u / a )
so integrating:
θ − θ i = − arccos ( a u ) ; a u = c o s ( θ − θ i )
reintroducing r :
r = 1 + e cos ( θ − θ i ) p
p = 8 L 0 2 > 0 , e = 1 + 3 2 m E 0 L 0 2 ≥ 0 , E 0 ≥ − L 0 2 3 2 m
substituting values for r 0 , v 0 , m , we get:
E 0 = − 2 7 , L 0 = 2 , p = 2 1 , e = 4 3
so the eccentricity is : e = b a = 4 3
a × b = 3 × 4 = 1 2
the equation of the trajectory is:
r = 4 + 3 cos ( θ − θ i ) 2
t 0 = 0 , r = r 0 = 2 , θ = θ 0 = 0 , so:
cos ( − θ i ) = − 1 , θ i = π , so the equation of the trajectory became:
r = 4 − 3 cos ( θ ) 2
using the equation of motion:
( d θ 2 d 2 r 1 + r 1 ) = L 0 2 8 m 2
imposing w = r 1 , c = L 0 2 8 m 2 , we get:
w ¨ + w = c , with general solution: r 1 = a 1 cos θ + a 2 sin θ + c
t = 0 , θ = θ 0 , imposing: a 1 2 + a 2 2 a 1 = cos θ 0 , a 1 2 + a 2 2 a 2 = sin θ 0 , a 1 2 + a 2 2 = A ,
we get:
r 1 = A cos ( θ − θ 0 ) + c , imposing: c = p 1 , A = p e ,
r = 1 + e cos ( θ − θ 0 ) p , the same equation of the trajectory.
I solved this problem numerically, using Euler's numerical method to find the particle as it moves along the force field. Here is an image that I made of the trajectory using 2000 data points from python simulated for 2.5 seconds and scatter plot:
As you can see, the particle does trace out an elliptical path. Calculating the value of e = a a 2 − b 2 , with the data, you roughly get 0 . 7 5 , which is equal to 4 3
Here is my python code below, which has timestep of 1 0 − 3 . Plot the data points in Excel.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
|
If we know that the trajectory is an ellipse as given in the question and given that it is an inverse square force,it must be directed towards one of the focii.
Therefore one of the focii is the origin.
further by shifting origin, x = ae + acos(wt)
y = bsin(wt)
at t=0
Vy = 1 => wb=1......(i)
acceleraton in x direction = 2 => w^2 * a = 2............(ii)
also distance of particle at t=0 from focs is a(1+e) = 2.........(iii)
Solving these three equation for e gives e = 3/4. Is it correct?
First thing we do is that we switch to polar co-ordinates r = r c o s θ i ^ + r s i n θ j ^
Also the velocity will have two components :
1)Tangential velocity = v t
2)Radial velocity= v r
Then we note that since the force is central hence angular momentum for the particle is conserved. So we write :
m v 0 r 0 = m v t r (i)
Also by conservation of total energy we have K.E+P.E.=Constant
2 1 m v 0 2 − r 0 8 = 2 1 m v 2 − r 8 (ii)
Also v t 2 + v r 2 = v 2 (iii)
Using (iii) in (ii) we get
2 1 m v 0 2 − r 0 8 = 2 1 m ( v t 2 + v r 2 ) − r 8
Using (i) to get
2 1 m v 0 2 − r 0 8 = 2 1 m v r 2 + 2 r 2 m v 0 2 r 0 2 − r 8
Put the values to get :
d t d r = v r = r 1 6 − r 2 4 − 7 (iv)
Also v t = ω r hence in (i) we have
ω r 2 = r 0 v 0
⇒ ω = r 2 2 = d t d θ (v)
Dividing eq. (iv) by (v) we have
d θ d r = 2 r 2 r 1 6 − r 2 4 − 7
⇒ ∫ r 1 6 r − 7 r 2 − 4 2 d r = ∫ d θ
C − tan − 1 ( 1 6 r − 7 r 2 − 4 2 ( 2 r − 1 ) ) = θ
Finding the constant of integration and putting it we have :
cot − 1 ( 1 6 r − 7 r 2 − 4 2 ( 2 r − 1 ) ) = θ
Solving for θ we have
r = 4 − 3 c o s θ 2
Polar equation of a general ellipse is given by r = 1 − e c o s θ l
e=eccentricity and l=latus rectum
Comparing it with our original equation we have :
e = 4 3