Solve it if you can #2
In the triangle ABC, if AB=6, AC=3 and the angle (B)=30 and D is the base of the bisector of (A), what is the distance between D to AB?
The answer is 1.73.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
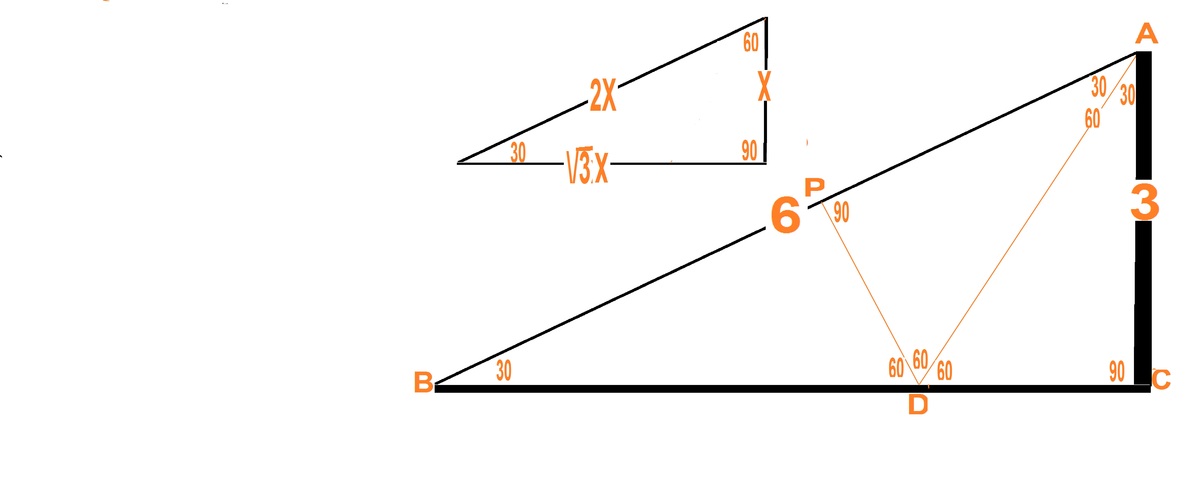 D
r
o
p
D
P
⊥
B
C
.
W
h
a
t
w
e
n
e
e
d
i
s
P
D
.
A
3
0
−
6
0
−
9
0
r
t
∠
d
Δ
i
s
s
h
o
w
n
i
n
t
h
e
s
k
e
t
c
h
.
From this we can see that ABC, ABD, APD are all 30-60-90
Δ
s
∴
i
n
Δ
A
C
D
,
A
D
=
2
3
.
∴
i
n
Δ
A
P
D
,
P
D
=
2
3
∗
2
1
=
1
.
7
3
D
r
o
p
D
P
⊥
B
C
.
W
h
a
t
w
e
n
e
e
d
i
s
P
D
.
A
3
0
−
6
0
−
9
0
r
t
∠
d
Δ
i
s
s
h
o
w
n
i
n
t
h
e
s
k
e
t
c
h
.
From this we can see that ABC, ABD, APD are all 30-60-90
Δ
s
∴
i
n
Δ
A
C
D
,
A
D
=
2
3
.
∴
i
n
Δ
A
P
D
,
P
D
=
2
3
∗
2
1
=
1
.
7
3
Why AD = 2√3?
Log in to reply
Δ A C D i s 3 0 − 6 0 − 9 0 . H y p o t . A D = 3 2 . A C = 3 2 ∗ 3 = 2 3 .
Log in to reply
I think BC= √6^2+3^2=√45=3√5. Because sin(30°)=0.5, AD=2 DC. Obviously ADC ≌ BPD, so BD=2 DC. Then DC=√5.
Log in to reply
@A Former Brilliant Member – B C = 6 2 − 3 2 = 3 3 .
Log in to reply
@Niranjan Khanderia – Oh lord, I get it now! I made a big mistake...
I think BD = 2DC. Obviously BC = √(6^2+3^2)=3√5. So DC = √5
Log in to reply
Why BD=2 * DC?
Log in to reply
Because sin(30°)=0.5, AD=2 DC. Obviously ADC ≌ BPD, so BD=2 DC.
Log in to reply
@A Former Brilliant Member – Sorry, you are correct. You have slipped in finding BC as I have commented above.
B C = 6 2 − 3 2 = 3 3 .
According to Sin theory, we have: s i n ( B ) ∣ A C ∣ = s i n ( C ) ∣ A B ∣ → C = 9 0 0 B C = ∣ A B ∣ 2 − ∣ A C ∣ 2 d D ∣ A B = ∣ A B ∣ + ∣ A C ∣ [ A B C ] = 1 . 7 3
According to a theorem: BD/CD=sin(BAD) ̂ /sin(DAC) ̂ ×AB/AC we replace AB=6 , AC=3 in the formula (we knew that angles BAD and DAC were equal so sin BAD=sin DAC) First=> 2CD=BD then we use cosines theorem: AC^2 = AB^2 + BC^2 -2 AB BC Cos ABC by replacing values of AB and BC and Cos ABC and solving the outcome quadratic equation, we will understand that: Second=> BC=3 3^(1/2) by the First and Second equations we can see that BD=2 (3^(1/2)). and its obvious that distance between D and side AB is equal to BD (1\2) means the distance is = 3^(1\2)