Some more Irodov revision for old Dougo

Classical Mechanics Level 2

This is one of my favourite problems from Irodov. It's really quite beautiful conceptually.

Here's the problem:

What is the minimum acceleration with which bar A (Fig. 1.22) should be shifted horizontally to keep bodies 1 and 2 stationary relative to the bar?

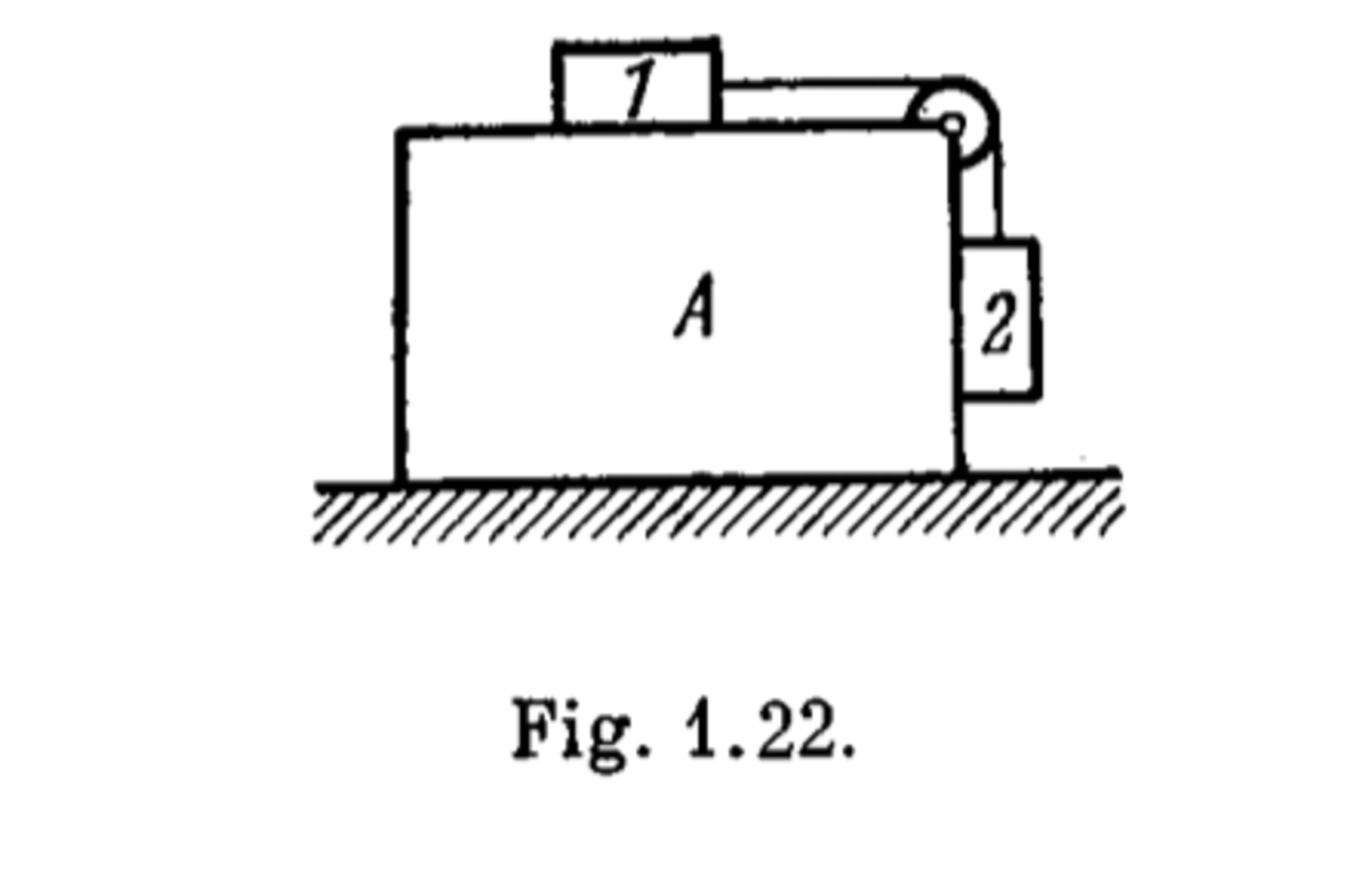
The masses of the bodies are equal, and the coefficient of friction between the bar and the bodies is equal to $\mu$ . The masses of the pulley and the threads are negligible, the friction in the pulley is absent.

The desired acceleration of the bar for the blocks to be stationary relative to the bar is of the following form:

$\displaystyle a = \frac{g(n-\mu)}{(p + \mu)}$

Type your answer as $n+p$ , where $n,p$ are positive integers.

The answer is 2.

1 solution

Krishna Karthik
Sep 22, 2020

Firstly, to understand what the acceleration of the bodies have to be if they are to be at rest in the bar's accelerated frame. Basically, the principle of this problem is that the bars have to be at an equal acceleration to appear stationary in the bar's reference frame.

If body 1 is not accelerating enough to the right direction, then it will "lag" behind; ie. it won't appear at rest. If it is accelerating more than the acceleration of the bar, then it will go too far and won't appear at rest. However, at just the right acceleration, block 1 will "move with the bar".

Writing the equation of motion for body 1:

$\displaystyle ma = T - \mu mg$

Where $a$ is the desired acceleration of block 1.

For block 2, note that the normal force is increased because the bar is sort of creating an artificial gravity by accelerating to the right at acceleration $a$ .

Hence the normal force will be present , and will be:

$N_2 = ma$

Equation of motion:

$\displaystyle 0 = mg - T - \mu N_2$

Solving will yield $\displaystyle a = \frac{g(1-\mu)}{(1+\mu)}$

Which book do you practice for higher physics?