Someone began with 50 cents

Let the starting amounts for $Anna$ , $Brenda$ , and $Cynthia$ be written as $(A,B,C)$

After round 1) they have $(A+A,B-A,C)=(2A,-A+B,C)$

After round 2) they have $(2A,2(B-A),C-(B-A))=(2A,-2A+2B,A-B+C)$

After round 3) they have $(2A-(A-B+C),-2A+2B,2(A-B+C))=(A+B-C,-2A+2B,2A-2B+2C)$

Since these are the same we can now write the triple equation

$A+B-C=-2A+2B=2A-2B+2C$

Equating the first and third of this triple equation and solving for A:

$A+B-C=2A-2B+2C$

$A = 3B-3C = 3(B-C)$

This means $A$ is a multiple of 3. 50 is not a multiple of 3, so A did not begin with 50 cents.

Substituting this A into the first and second of the triple equation gives

$(3B-3C)+B-C=2B-2(3B-3C)$

$8B=10C$

$4B=5C$

This means $B$ is a multiple of 5 and $C$ is a multiple of 4. 50 is a multiple of 5 but not of 4. So $\boxed{Brenda}$ began with 50 cents.

And for the record, their starting amounts were $(30,50,40)$

I looked at the problem in reverse so that I only needed to look at one variable. Suppose that $x$ is the money that each of the three players have at the end.

Look at the third game. Cynthia wins against Anna and doubles her money. That means that, before game 3, Cynthia had $\frac{x}{2}$ . This also happens to be the amount that Anna loses. So, Anna had $\frac{3x}{2}$ before game 3. Brenda had $x$ since she did not participate in this game.

Now, look at game 2. Brenda wins against Cynthia and doubles her money. That means that, before game 2, Brenda had $\frac{x}{2}$ . This also happens to be the amount that Cynthia loses, putting her money at $\frac{x}{2}+\frac{x}{2}=x$ before this game. Anna still has $\frac{3x}{2}$ .

Finally, look at game 1. Anna wins against Brenda and doubles her money, meaning that Anna had $\frac{3x}{4}$ before this game. Brenda lost this amount, so she had $\frac{x}{2}+\frac{3x}{4}=\frac{5x}{4}$ initially. Cynthia still has $x$ .

Now, one of them has $50$ cents initially. If you set each of the initial amounts of money we derived above to $50$ , you will get that only Brenda's amount makes sense (others give fractional values for $x$ , which is absurd).

BTW, with this, you can find that all players had $x=40$ cents in the end, Anna had $\frac{3x}{4}=30$ cents initially, Brenda had $\frac{5x}{4}=50$ cents initially, and Cynthia had $x=40$ cents initially.

Let Anna, Brenda, and Cynthia start with $A(0)=a$ , $B(0)=b$ , and $C(0)=c$ respectively. Then we have:

$\begin{array} {clllll} \text{Round }n & Anna & Brenda & Cynthia \\ \hline 0 & A(0) = a & B(0) = b & C(0) = c \\ 1 & A(1) = 2a & B(1) = b-a & & \text{Anna wins.} & b > a \\ 2 & & B(2) = 2(b-a) & C(1) = c-b+a & \text{Brenda wins.} & c > b-a \\ 2 & A(2) = a+b-c & & C(2) = 2(c-b+a) & \text{Cynthia wins.} & 2a > c-b+a \end{array}$

Then we have

$\begin{aligned} A(2) & ={\color{#3D99F6}B(2)} = C(2) \\ a+b-c & = {\color{#3D99F6}2(b-a)} = 2(c-b+a) \\ \implies 2(b-a) & = 2(c-b+a) \\ b-a & = c - (b-a) \\ \implies c & ={\color{#3D99F6}2(b-a) = B(2)} = A(2) = C(2) \\ b - a & = \frac c2 & \small \color{#3D99F6} ...(1) \\ a+b-c & = c \\ a+b & = 2c & \small \color{#3D99F6} ...(2) \\ \implies b & = \frac 54 c & \small \color{#3D99F6} ...(1)+(2) \\ \implies a & = 2c - b = \frac 34c & \small \color{#3D99F6} ...(2) \end{aligned}$

Therefore $a: b : c = \frac 34 : \frac 54 : 1 = 3:5:4 = 30 \text{ cents} : {\color{#3D99F6}50 \text{ cents}} : 40 \text{ cents}$ . Therefore $\boxed{\text{Brenda}}$ started with 50 cents.

Work backwards. At the end, the three players' balances ( $Anna : Brenda : Cynthia$ ) are in the ratio $1:1:1$ .

Cynthia wins the final game, thereby winning half of her resulting balance off Anna. So the ratio immediately prior to this is $\frac32 : 1 : \frac12 = 3 : 2 : 1$ .

Brenda wins the second game, thereby winning half of her resulting balance off Cynthia. So the ratio immediately prior to this is $3 : 1 : 2$ .

Anna wins the first game, thereby winning half of her resulting balance off Brenda. So the ratio immediately prior to this is $\frac32 : \frac52 : 2 = 3 : 5 : 4$ . This is thus the ratio of funds that they start with.

Since $3 : 5 : 4$ is a ratio in its lowest terms, and since each person starts with an integer number of cents, then their opening balances must be $3n$ , $5n$ and $4n$ respectively for some integer $n$ . Of these, only $5n$ can equal 50, thus $n = 10$ . So the amounts they start with are:

• Anna - 30 cents
• Brenda - 50 cents
• Cynthia - 40 cents

Each player has 3 different amounts of money throughout the game, Which I'll write as $A_{1}, A_{2}, A_{3}$ for Anna, etc.

The results of the games show us:

$A_{1}=A_{2}\div2$

$B_{1}=B_{2}+A_{1}$

$C_{1}=C_{2}+B_{2}$

$A_{2}=A_{3}+C_{2}$

$B_{2}=B_{3}\div2$

$C_{2}=C_{3}\div2$

Substitution gives us:

$A_{1}=(A_{3}+(C_{3}\div2))\div2$

$B_{1}=(B_{3}\div2)+(A_{3}+(C_{3}\div2))\div2$

$C_{1}=(C_{3}\div2)+(B_{3}\div2)$

As $A_{3}=B_{3}=C_{3}$ , we can replace these with $x$ , and cancel down the equations:

$A_{1}=\frac{3}{4}x$

$B_{1}=\frac{5}{4}x$

$C_{1}=x$

Since all these must be integers (as cents are indivisible), only $\boxed{Brenda}$ can start with 50 cents; if $A_{1}$ or $C_{1}$ are 50, the other will not be an integer.

If you make a table how the game develops when assuming Anna has the 50c, you get the table as shown below: Where p is the resulting money each players has at the end of the game.

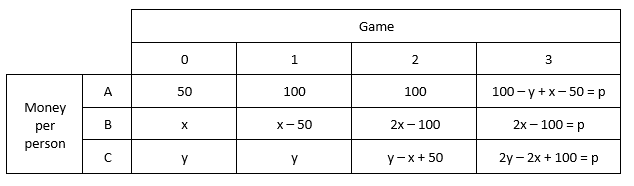
When you put the last collum into a matrix and do the RREF tranfsformation you get non integer solutions. Hence Anna (=A) can't have the 50c in the beginning of the game.

When you make the same table but assume Brenda has the 50c at the start of the game, you get the table as shown below:

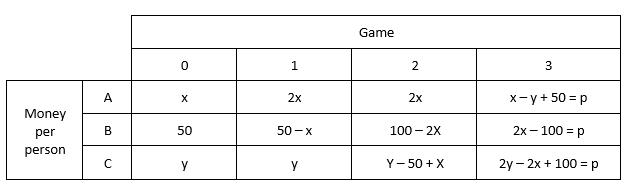
After the RREF transformation you'll see that x = 30 thus Anna has 30c at the beginning of the game and y = 40 thus Brenda has 40c.

Playing the game with these numbers gives you the result that all players end the game with 40c.

Let's call the three starting amounts $a,b,c$ .

Then the game progresses like this: $a, b, c \\ 2a, B, c \\ 2a, 2B, C \\ 2a-C, 2B, 2C \\$

where $B = b-a$ and $C = c-B$ , and with $a \geq 0$ and $B \geq 0$ and $C \geq 0$ and $2a-C \geq 0$ .

On the way we changed coordinates from $(a,b,c)$ to $(a,B,C)$ to eliminate some unnecessary writing.

Since $2a-C = 2B = 2C$ , we find $B=C$ and $2a=3C$ . These equations have only the solutions $(a,B,C) = (3n,2n,2n)$ . Back to original coordinates: $(a,b,c) = (a, a+B, B+C) = (3n, 5n, 4n)$ . This Diophantine equation has entirely integer solutions only for $n$ integer.

Since 50 is not divisible by 4 nor 3, only $b$ can be 50 for $n$ integer. So $(a,b,c) = (30, 50, 40)$ and the answer is Brenda.

I was particularly lazy:

#!/usr/bin/env python

import numpy as np
from functools import reduce

def g(w,l):
    a = np.identity(3)
    a[w][w] += 1   # winner gets amount winner had
    a[l][w] -= 1   # loser loses amount winner had
    return a

m = reduce(np.matmul,[g(2,0),g(1,2),g(0,1)]) # reverse
i = np.linalg.inv(m)
print (np.matmul(i,[[1],[1],[1]]))*40  # 40 was added after inspection.

No algebra, just a little arithmetic and logic: Assume they all ended with $1.00 and play the game backwards. Doing so is easy and you find that Anna would have started with $.75, Brenda with $.50 and Cynthia with $1.00. The ratio of these amounts must be the same no matter how much they all start with. So, we scale all three numbers by the same factor to reach $.50 for Anna, and do the same for Brenda, and finally for Cynthia. Only when you scale these numbers (by 2/5) to give Brenda $.50, do the other two players end up with an integer number of cents. In this case, Anna starts with $.30 and Cynthia starts with $.40.