This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
Great question!
Log in to reply
What do you mean by "Again fish"?
Log in to reply
Again your favorite thing in the title XD!!!
Log in to reply
@Atul Shivam – Who said fish is my favorite thing? :P
but this relation is true for 2 so you can't categorize it under false for all positive integers
Log in to reply
The question stated "All positive real values of x ."
It is not true for all of them, so the answer is False
Just the main thing is, x x x x = ( x x x ) x 1 Rest follows!!
To me, it seems as though it can be true or false depending on which positive real number you choose. The statement is true for cases where x is equal to 1 or 2, and false for cases where x is neither 1 nor 2. To claim that an open statement like that is always true or always false is illogical. If it said something like, "for all x in the set of positive reals, P(x)", then I could see an argument for claiming that the existence of counterexamples would cause that closed statement to be false. But as we are not told any restrictions on x other than the fact that it is a positive real number, there is insufficient data to produce a definite answer.
It will be correct for 2 so it can't be characterised as false
Correct :+1: upvoted!!!
You are wrong! This is absolutely true. Your solution's 4th step doest really equals to 5th step, when multiplied by inverse function it becomes 1. So This is absolutely true. Try with any possible integer. :) Good Day!
Log in to reply
No nihar is absolutely correct!
Log in to reply
Not at all. :)
No Brother. :) Try with examples or I will simplify it and give it to you :)
Log in to reply
@Soham Ganguly – Try with 0.1 and look brother
Log in to reply
@Ashish Menon – Look brother. Mathematical Inequations can't be proved with examples. I am simplifying this for you.
x^x^x is equals to x^x-square. when rooting with power x this whole equation becomes x^x-square^1/x=x^x^(2-1)=x^x. I dont know how to format this :(
Log in to reply
@Soham Ganguly
–
So this might be the place where you are going wrong.
(
x
x
x
)
x
1
=
x
x
It is actually equal to
x
x
x
×
x
1
=
x
x
x
×
x
−
1
=
x
x
x
−
1
We have to multiply the top exponent with all of the base given because Nihar's question's LHS can also be written as
(
(
x
)
x
x
)
x
1
Log in to reply
@Ashish Menon – Just tell me how x^x^x^x^-1 is is equals to x^x^x^-1
Log in to reply
@Soham Ganguly – There is a multiplication sign between the last 2 x's of the LHS
Log in to reply
@Ashish Menon – Now I am giving you a proper thing Wait! x x x x − 1 = x x 1 or x x 2 ⋅ x − 1 = x x 2 − 1 = x x 1 = x x
@Ashish Menon – When extreme top orders are multiplying what is the solution? How can x X x^-1 = x^-1
Log in to reply
@Soham Ganguly – That is the mistake! We have to multuply the entire exponent if the base with the one outside the bracket.
@Soham Ganguly – How x ⋅ x − 1 is equals to x − 1 Oh I Did It :D ;)
Log in to reply
@Soham Ganguly – I didnt understand did you understand how to solve this problem?
@Soham Ganguly – Can I know why x x x = x x 2 ?
Note that x x x = ( x x ) x
Log in to reply
@Hung Woei Neoh – Yes, maybe he has got tower rule confused.
Log in to reply
@Ashish Menon – No, he definitely got his tower rules confused. It was rather obvious from his statement.
Do check out the rules to evaluating tower exponents. We always start from the highest exponent, that is:
x x x = x ( x x ) = ( x x ) x
Ask yourself, is 3 3 3 and ( 3 3 ) 3 the same thing?
I know I am wrong :( But why would 16 people upvote a wrong solution and the challenge master note does not mention any mistake? :(
Log in to reply
If this is not a sarcastic reply then I am really interested to report it to a mod. :) Its better if you go & do it. I saw this was shared by brilliant.org through fb page. This just ruins their reputations. :)
Log in to reply
@Soham Ganguly – I think you dont know but nihar himself is a mod
Try yourself by putting in any integer. It is NOT true.
Log in to reply
Lets take 2. 2^2^2=16. Square Root of 16 is equals to 4 i.e. 2^2 In Case of 3. 3^3^3=19683. Cube Root of 19683 is indeed 27 i.e 3^3
Log in to reply
@Soham Ganguly – Positive real number does not only mean that you have to use positive integers, substitute 0.1 and look you wont get the same answer. :)
May I know how did you conclude that the 4rth step of Nihar's solution is not equal to his 5th step? I dont find any errors. Plz explain your viewpoint.
Log in to reply
When multiplied by inverse it becomes 1. Sin X Sin^-1 is equals to 1. x X x^-1 is equals to 1. :)
You got your rules of exponents confused. Here, I'll show you an example:
Say x = 3
x x x x = 3 3 3 3 = ( 3 2 7 ) 3 1 = 3 2 7 × 3 1 = 3 9 = 3 3
Shouldn’t it be 3^3^3 = (3^3)^3=27^3 rather than 3^27?
Log in to reply
No. When dealing with multiple exponents (as it is in the case of 3 3 3 ), you start from the highest exponent and work your way down. So, in the case of 3 3 3 , it would be 3 ( 3 3 ) = 3 2 7 . You can also try it on a calculator, like desmos.com. Type in 3 3 3 (without any parenthesis) and it should equal 3 2 7 = 7 . 6 2 5 5 9 7 4 8 5 × 1 0 1 2 .
x x x x = ( x x x ) x 1 = ( x ( x x ) ) x − 1 = x ( x x ) ( x − 1 ) = x x x + − 1 = x x x − 1
Fixed typo in @Nihar Mahajan
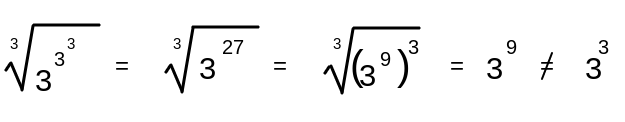
Relevant wiki: Rules of Exponents - Algebraic
x x x x = ( x x x ) x 1 = ( x x x ) x − 1 = x x x × x − 1 = x x x − 1 = x x
If you have any queries, first review Rules of Exponents wiki and then comment below.