Spaceship Orbit
How fast ( in m/s ) does a spaceship need to orbit around Earth to not spiral down or fly away from it?
Details and Assumptions:
- The spaceship is 4 0 0 k m above the surface of Earth.
- Earth's radius is 6 3 7 1 k m .
- Gravitational acceleration on the spaceship is 8 . 6 9 m / s 2 towards the center of Earth.
The answer is 7670.722912.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Gah, forgot to convert to m/s. Shame on me 😅
The ISS is 400 miles up traveling at 4.75 m/s that is about 17,000 m/h this equation has a speed over 460,000 m/h, someone should inform NASA.
Log in to reply
You seem to be confusing metres with miles. The ISS travels at 4.75 miles/second but the answer in the example given is 7670.723 metres/second and when you convert the two speeds to the same units, they end up roughly equal. Whenever you see 'm/s', this always means metres per second. Miles per second would be written either as mi/s or just miles/sec.
Log in to reply
Thank you for clearing that up, that's why my answer was wrong.
Is there a way to show this result without using the (ficticious) centripetal force formula ?
For curious, here's the derivation of magnitude of centripetal (centrifugal) acceleration:
First, let us write parametric equation of the circle in Cartesian coordinates and evaluate some basic properties:
r ( t ) = r 0 ( i cos ( w t ) + j sin ( w t ) ) v = d t d r = r 0 w ( − i sin ( w t ) + j cos ( w t ) ) v = ∥ v ∥ = r o w v = − i sin ( w t ) + j cos ( w t ) ∣ ∣ ∣ ∣ d t d v ∣ ∣ ∣ ∣ = w
The last statement could be achieved geometrically too.
Now, applying product rule yields the formula:
v = v ⋅ v d t d v = d t d v v + v d t d v = v w = r 0 v 2 .
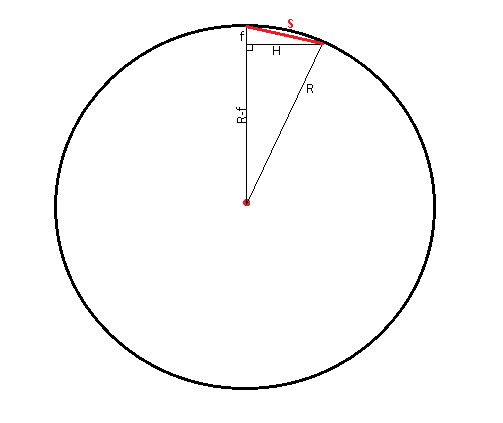
Is this wrong? : for 1 second the spaceship will fall towards the center of the Earth f=4.345 meters (8.69 / 2). Now the distance that the spaceship needs to cover, to stay in orbit (on the circle with radius R = 6771km ), for the same time: will be H. From here we can find H by Pythagoras' theorem where R^2 = (R-f)^2 + H^2 => H^2 = 2 R f - f^2. However since the distance (S) that will be traveled is on the circle (between the initial point and the end on) we can find it again using Pythagoras' theorem: S^2 = H^2 + f^2. From before we have H^2, so: S^2 = 2 R f = 6771000*8.69 => S ~ 7670.723 meters. As this distance needs to be covered per second this is also the answer for the speed of travel.
Log in to reply
I am not sure what you are writing. But an object in an orbit is actually in free fall. The distance falling toward Earth's center is balanced by the tangential distance as an end result the object moves in an orbit. That is why if the tangential velocity is lower the object falls to Earth. If it is higher it flies into space.
Log in to reply
Log in to reply
@Milko Dyakov – I suppose it means the same as I mentioned.
Log in to reply
@Chew-Seong Cheong – First i thought that the speed will be H "per second" (very close guess), as this is what is needed to compansate in order to stay in orbit (on the circle) perpendicularly, as you do not need additional force to fall. However - the actual distance traveled is S - and this is the answer. Feels a bit odd, as the actual distance is on the curve, so longer path = greater speed, but also H will be the needed perpendicular force, so lower speed/push in that direction. I guess S is in the midde of these 2 :) ...and - No i am not sure what I mean :( - i just got the answer like this, no force, just distance that needs to be covered. This is why i ask ...
Log in to reply
@Milko Dyakov – I read all your comments. Your reasoning is close to correct and it would have been totally correct if you had used infinitesimals. Your mistake lies in the fact that you assume that the direction of the gravitational force and object's velocity are constant over the period of one second while the truth is that they are both continuously changing.
Log in to reply
@Uros Stojkovic – Yeah, probably - i thought about that ... but then the point on the circle is chosen so the ship is there after 1 second being constantly in orbit - so the gravitational force shuold be constant all the way. And 4,345 meters will be the distance covered for object that have no initial velocity with that acceleration for 1 sec. (free fall). Anyway - i am sure that i am missing something. I just wonder why S in the picture is the right answer :)
Log in to reply
@Milko Dyakov – Gravitational acceleration (force) vector has constant magnitude but not constant direction. So, if there's initial tangential velocity, you must take it to account because continuous change of position causes continuous change in gravitational vector's direction. Your model yields correct speed value, but fails to accurately model the circular motion. Moreover, your method doesn't yield a tangential velocity, normal to radius at certain point. See my comment below for rigorous approach.
The spaceship will remain in orbit so long as the magnitudes of the centripetal and gravitational forces acting on it balance, that is F c = F g r m s v 2 = r 2 G m s m e where m s is the mass of the spaceship and m e is the mass of the earth m e = 5 . 9 7 2 ⋅ 1 0 2 4 k g , and G is the gravitational constant G = 6 . 6 7 ⋅ 1 0 − 1 1 k g 2 N m 2 . Solving for velocity gives v = r G m e , where r = ( 6 3 7 1 + 4 0 0 ) ⋅ 1 0 3 m v = ( 6 3 7 1 + 4 0 0 ) ⋅ 1 0 3 6 . 6 7 ⋅ 1 0 − 1 1 ⋅ 5 . 9 7 2 ⋅ 1 0 2 4 ≈ 7 6 7 0 .
The centripetal force is aimed in the same direction as gravity. In fact, gravity serves as the required centripetal force. So I don't think you should state that they should balance. I would formulate it as "The spaceship will remain in orbit as long as the required centripetal force is generated by the gravity acting on it."
Log in to reply
True, at my school my physics teacher would have crossed the whole answer just for such a simple wording mistake...
Surprisingly very well said.
Not perfect enough. just use v^2=gR ,don't need the m of earth
In order to let the spaceship at 400 km height (above ground) go around the earth without spiraling down/flying away from it, the centrifugal force on the spaceship has to be equivalent to / delivered by the gravitational force. So:
F c = F g
r + h m v 2 = m ⋅ ( r + h ) 2 G M , where m is the mass of the spaceship (kg), M is the mass of the earth (kg), v is the velocity of the spaceship (m/s), G is the gravitational constant ( 6 . 6 7 ⋅ 1 0 − 1 1 N m 2 k g − 2 ) , r is the radius of the earth (m) and h is heigth of the spaceship above the ground (m).
M is not given, but we still can use that a = 8 . 6 9 m/s 2 , because ( r + h ) 2 G M = a .
Plugging this last formula in the original equation will result into:
r + h m v 2 = m ⋅ a , where a is the acceleration which is pulling the spaceship down were it not moving forward (m/s 2 ).
Multiplying both sides by ( r + h ) / m , will give us v 2 = a ( r + h ) , which means v = + a ( r + h ) = 8 . 6 9 ( ( 6 3 7 1 + 4 0 0 ) ⋅ 1 0 3 ) ≈ 7 . 6 7 ⋅ 1 0 3 (m/s).
Solution with no physics formulas only basic calculus:
Let t be the number of seconds after the rocket was directly right of Earth (0 degrees). Let x ( t ) and y ( t ) be the be rocket's position relative to the center of the Earth in meters. The given details show us that x ( 0 ) = 6 7 7 1 0 0 0 and x ′ ′ ( 0 ) = − 8 . 6 9 . Let z be the number of seconds it takes the rocket to orbit the earth.
x ( t ) = 6 7 7 1 0 0 0 cos ( z 2 π t )
x ′ ′ ( t ) = − 6 7 7 1 0 0 0 ( z 2 π ) 2 cos ( z 2 π t )
Plug 0 into x ′ ′ ( t ) :
− 8 . 6 9 = − 6 7 7 1 0 0 0 ( z 2 π ) 2
8 . 6 9 6 7 7 1 0 0 0 = ( z 2 π ) 2
z = 2 π 8 . 6 9 6 7 7 1 0 0 0
The distance the rocket travels is given by 2 π r where r is the distance to the center of the earth. Plugging in r we get: 1 3 5 4 2 0 0 0 π Now that we have the distance in meters and time in seconds it takes to orbit the earth, we can just take t i m e d i s t a n c e to find the velocity.
1 3 5 4 2 0 0 0 π 2 π 8 . 6 9 6 7 7 1 0 0 0 = 7 6 7 0 . 7 2 3
Great approach. I much prefer this to trying to figure out which physics formulas need to balance out.
I'm not familiar with orbital equations and I don't know the formula for centripetal force, but I have a basic understanding of physics and math, so my solution just uses the Pythagorean theorem, limits, and an equation of motion.
The ship is distance r from the center of the earth.
The ship moves forward some distance d over a time period Δ t
Using this equation of motion x = x o + v t + 2 1 a t 2 we find the ship then falls towards the earth for a distance 2 1 g Δ t 2 and since the ship is orbiting, the remaining distance to the center is r
This forms a right triangle, thus we can use the Pythagorean theorem to find d 2 + r 2 = ( 2 1 g Δ t 2 + r ) 2 ⟹ d = ( 2 1 g Δ t 2 + r ) 2 − r 2
Now, in reality the ship falls toward the earth at the same time that it is moving, so there is some error. But the error gets smaller as Δ t gets smaller.
So we can find the speed using the equation S = lim Δ t → 0 d / Δ t = lim Δ t → 0 ( 2 1 g Δ t 2 + r ) 2 − r 2 / Δ t
⟹ S = lim Δ t → 0 4 1 g 2 Δ t 4 + r g Δ t 2 + r 2 − r 2 / Δ t
⟹ S = lim Δ t → 0 4 1 g 2 Δ t 4 + r g Δ t 2 / Δ t
⟹ S = lim Δ t → 0 Δ t 4 1 g 2 Δ t 2 + r g / Δ t
⟹ S = lim Δ t → 0 4 1 g 2 Δ t 2 + r g
⟹ S = r g
Plugging in the values r = 4 0 0 0 0 0 m + 6 7 3 1 0 0 0 m and g = 8 . 6 9 m / s 2 give the answer S = 7 6 7 0 m / s
g = v 2 / R where g = 8.69 m / s 2 and R =400000+6371000 m
thus v = s q r t ( m R )
so v = s q r t ( 8 . 6 8 × 6 7 7 1 0 0 0 ) =7671.7229
It is worth pointing out that this is the required speed for a circular orbit. There is a range of lower speeds that would result in an elliptical orbit with an apogee of 6771 km.
Also, too slow a speed would not result in a spiraling descent, merely an ellipse whose perigee would be less than 6371 km, resulting in a bad day for the astronauts.
I have addressed this issue about a circular orbit previously although I can't seem to adjust the problem.
in a circular trajectory there is always an acceleration which direction is the center, even if the motion has constant velocity. This acceleration has a value of:
a = r v 2
a : acceleration.
v : velocity.
r : radius of the circular trajectory
As we can imagine the only acceleration which keeps the rocket orbiting the planet in a constant circular trajectory is the gravity, so we can construct the next equation:
g = 8 . 6 9 = r v 2
now we need the radius of the circular trajectory to get the velocity we need. We obtain this radius adding the distance between the earth surface and the rocket, with the earth radius, as following:
r = 4 0 0 [ k m ] + 6 3 7 1 [ k m ] = 6 7 7 1 [ k m ] = 6 7 7 1 [ k m ] ∗ 1 [ k m ] 1 0 0 0 [ m ] = 6 7 7 1 0 0 0 [ m ]
We transform it into meters because we are asked to give the result in s m , and we have to be congruent with the units. Now we can find the velocity with the equation we have constructed:
v = 8 . 6 9 [ s 2 m ] ∗ 6 7 7 1 0 0 0 [ m ] = 7 6 7 0 . 7 2 2 9 1 2 [ s m ]
Actually, there is a flaw in the question. If the spaceship is orbiting at a fixed distance from the centre of the earth, gravitational acceleration " ON THE SPACESHIP " would be zero(experiencing free fall). Instead, it should have been given that the gravitational acceleration is 8.69m/s2 at that height.
Check the definition of free fall.
Instead of using the fact that the force of gravity and the centripetal force have to be equal. I used the equation for centripetal acceleration a c = r v 2 . Then I solved for v to get the equation v = r a c . Then, I plugged in the value for the centripetal acceleration (which is the gravitational acceleration in this case). And for the radius of the rotation. Which is the radius of the orbit plus the radius of the earth; because the radius we put into our formula has to be the same as the radius of orbit if the earth was just a point with the same mass as the earth. Plug the values in and one gets 7 6 7 0 . 7 2 ⋯
As a motion in a curved path involves changing of direction of the velocity vector, it is an accelerated motion. It requires a force toward the center of curvature called centripetal force given by F c = r m v 2 , where m is the mass of the object in motion, v , the velocity of the object and r , the radius of curvature.
If F c > m g , where g is the acceleration due to gravity, then the object will spin off the curve. If F c < m g , the object will move towards Earth. For the object to stay in orbit, then F c = m g . Then r m v 2 = m g , ⟹ v = r g = ( 4 0 0 + 6 3 7 1 ) 1 0 3 × 8 . 6 9 ≈ 7 6 7 0 . 7 2 3 .