Sphere Cylinder intersection, what is the arc-length of the intersection?
This problem’s question: Sphere Cylinder intersection, what is the arc-length of the intersection?
The sphere is of radius 2 centered at the origin.
The cylinder is parallel to the z -axis, of radius 1 and centered at {1,0,?}.
The arc length is requested for the +++ octant only, i. e., x ≥ 0 , y ≥ 0 , z ≥ 0 .
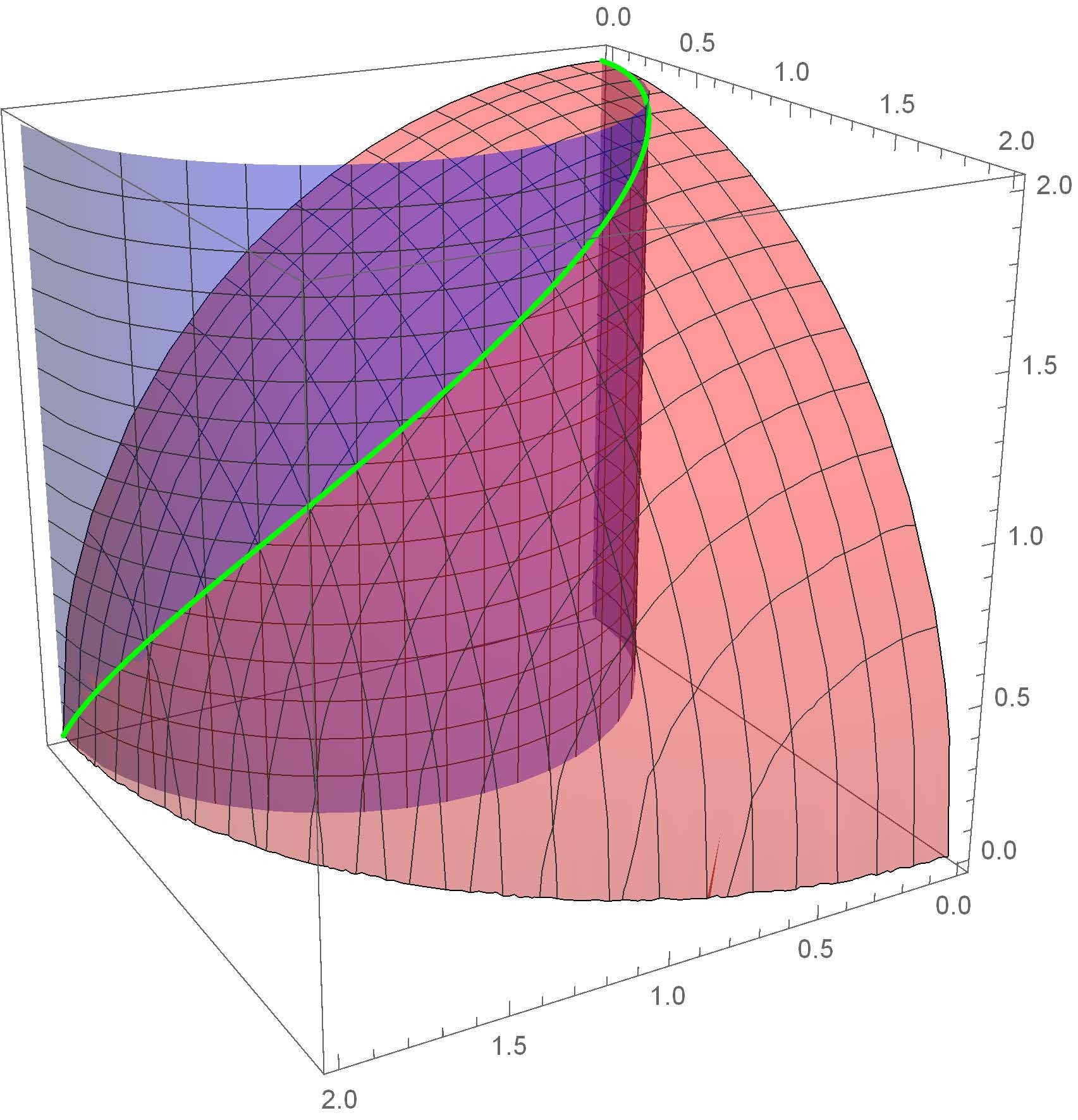
The answer is 3.82019778902771.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Yes, you are correct. Note, in my solution, a closed form solution was provided. That solution is a numerical integration, which is sufficient to answer the problem.
You referred to another problem and its solution. That other solution was a numerical integration.
"int sqrt (1+(sin(t)^2/(2+2cos(t))))dt from t=0 to t=pi" was your Wolfram/Alpha input.
It took an hour to make what you said intelligible.
∫ 2 cos ( t ) + 2 sin 2 ( t ) + 1 d t ⇒ 2 E ( 2 t ∣ ∣ − 1 )
2 E ( 2 0 ∣ ∣ − 1 ) ⇒ 0
2 E ( 2 π ∣ ∣ − 1 ) ⇒ 2 E ( − 1 ) ≈ 3 . 8 2 0 1 9 7 7 8 9 0 2 7 7 1 2 0 1 7 9 0 4 7 6 2
The E function is the Mathematica EllipticE function. which is also documented, slightly diffrently, in Wikipedia as Complete elliptic integral of the second kind .
2 E ( − 1 ) ⇒ 3 . 8 2 0 1 9 7 7 8 9 0 2 7 7 1 .
The E function is the Mathematica EllipticE function. which is also documented, slightly diffrently, in Wikipedia as Complete elliptic integral of the second kind .
I believe it should also be mentioned that the radius of the cylinder is 1
Oops, my mistake. You caught not one, but two mistakes. If I had included the image as well, then the radius would have been reasonably obvious. Good catch.
This is Viviani's curve (or at least part of it).
Yes, exactly.
BTW, e x = x ! has two solutions, both non-negative.
Log in to reply
Sounds like a different problem - I won't give anything away here in case people see this first, but the non-negative solution at x = 0 was discounted in the problem's wording (it asks for positive solutions). The other (ie the solution to the problem) is fine, except care was needed in extending the factorial function to non-integer parameters - there's more than one way to do that. Or did you mean another solution?
Log in to reply
Yes, another problem. I know of no other way of communicating with you without disclosing either your or my email.address. I solved the problem today. I withdrew my report against the problem when I realized what the author meant. The wording is in fact correct. The author has edited the problem and added a hint which handles the issue of extending the factorials to non-integers. The problem only requires a numeric answer.
Log in to reply
@A Former Brilliant Member – The wording was changed from the original and is now correct (the original wording had some ambiguity which has now been fixed)
I use Wolfram
Same problem is here