Spiral length
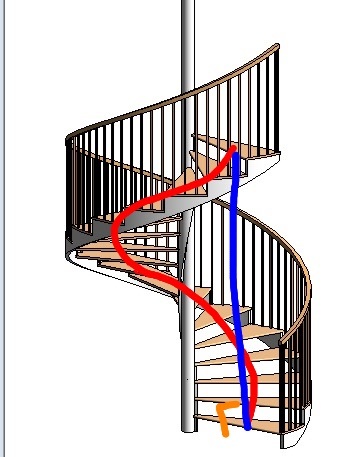In the above picture, the length of the blue line, which is perpendicular to the ground and touches the red line at both end points, is 10 feet and the distance from the center pole to the red line is 2 feet. When looked at from directly above, the red line SEEMS as if it forms a circle.
Find the length of the red line rounded to the nearest tenth IN FEET
Note: this problem was inspired when I was at my best friend's house and I asked him what the length of his stair case was to which he promptly responded and called me a nerd XD.
The answer is 16.1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
How u put radius as '2'??
Log in to reply
Because the spiral has a constant distance from the polemic 2 feet.
I used Differential Geometry technique. Standing at the central pole and looking up, One can see that the red line forms a circle Circumference of circle =s = 2πr As the distance from red line to central pole = 2 feet => radius = 2 feet => s = 4π I assume that this shape forms a cylinder and cylinder is the combination of circular rings. And length of each ring = 4π and as given length of blue line = 10 => 4π × 10 = 125.6 My answer is not correct. I don’t know where I have done mistake. Please improve
Log in to reply
You solved for the lateral surface area. You need to solve for the length of the line by doing the Pythagorean theorem.
Duh!! I gave my answer in inches!! (192.7") which is the same as 16.1 feet. So I consider my answer correct ;)
Apparent circle has a circumference of 2(pi)(r) =48pi = 150.816 inches
There are 18 treaders separated by 17 vertical gaps (risers) and 17 of the treaders complete the full circle.
Consider the red line as being composed of 17 sections each acting as the hypotenuse of 17 identical and vertical right-angled triangles. In relation to the angle of ascent, the riser acts as the opposite side and the treader as the adjacent side.
Each riser (opposite side) is 120/17 inches = 7.0588 inches. Where the red line touches, each treader (adjacent side) is 150.816/17 inches = 8.8715 inches
Using Pythagoras, each of the 17 hypotenses is 11.3371 inches.
So length of red line is 192.73 inches, = 16.1 feet
I did it the same way. Here is an animation showing how the helix (or a helical 'thread' of a screw) can be unwound to get the inclined plane (in context of simple machines). https://www.youtube.com/watch?v=9qFI9tOIOC4
Can't we use the helical spring formula! √[(πnd)^2+L^2] where n= no. Of turns of spring d= dia of spring L= length of spring As given L=10 D= twice of radius I.e. 4 N as shown in fig. No. Of turns 2!! But the answer m getting is 27.03 !
The equation u have posted above is similar but I guess you have taken diameter as 2?? But the dia should be 4?? Or the no. Of turns as 1?? Or 2??
Log in to reply
number of turn = 1.
It's because the length is not 10, the height is 10
Same solution :D
Just as an alternative to Trevor's approach, (and to be extra nerdy), we can look at this as a calculation of the arclength of a 3-D curve.
With the central pole acting as the z -axis and the bottom stair lying on the x y -plane, the red curve then has the parametric equations
x = 2 cos ( t ) , y = 2 sin ( t ) , z = ( π 5 ) t ,
where the parameter t goes from 0 to 2 π .
The length of the red curve, (a helix ), will then be
∫ 0 2 π ( x ′ ( t ) ) 2 + ( y ′ ( t ) ) 2 + ( z ′ ( t ) ) 2 d t = ∫ 0 2 π 4 + π 2 2 5 d t =
2 ∗ 4 π 2 + 2 5 = 1 6 . 1 feet to the nearest tenth.
Nice solution. That's what I did. I knew this because I have done this before while studying the motion of a charged particle in a uniform magnetic field. Nice problem though!
Wowwww. Nice solution. I was just wondering the other if integration worked in polar coordinates. This was my first approach, but since I'm not the best at polar coordinates, I resorted to a more geometric approach (I'll post it now)
Log in to reply
Thanks. I knew you were going to handle the elegant, intuitive method, (converting a space curve problem into a plane curve one), so I thought I'd take the parametric approach for variety's sake.
Log in to reply
You never cease to amaze me with your solutions
Also, I thought that the length of a graph can be the integral of the square root of the function+1.
Log in to reply
@Trevor Arashiro – In two dimensions the arc length of curve y = f ( x ) from x = a to x = b is given by the formula
∫ a b 1 + ( y ′ ) 2 d x .
I suspect this is the formula you were thinking about. :)
Log in to reply
@Brian Charlesworth – Ah, I see it's only for the 2D case. Thanks for that.
How did the z = 5/pi t come ?
Log in to reply
Since I wanted z to go from 0 to 1 0 linearly as t goes from 0 to 2 π . (This ensures a constant curvature for the helix.) So at t = 2 π we have z = ( p i 5 ) ∗ 2 π = 1 0 , as desired.
Log in to reply
Thanks. I was thinking of t on a 2-d plane, since x and y can be considered as the projection of the spiral, but wasn't able to figure out how to get z in. How should we interpret t physically, as in which angle should it be, or is it just a parameter ?
Log in to reply
@Indranil Chakraborty – Taking the angle as t is the easiest way to parameterize this problem. Essentially we're working with cylindrical coordinates here, which is basically the 3D version of polar coordinates.
One way to physically interpret this curve is as follows. Imagine you're holding in front of you a 2-foot long rope with a weight at the end. You start swinging the rope in front of you so that the weight traces out a complete vertical circle every 2 π seconds, (which would be abnormally slow, but this is just to help in visualizing, so ....). While doing this you then start walking in a straight line at π 5 feet per second. So after 2 π seconds you've simultaneously traced out a full circle in your frame of reference and also walked 1 0 feet forward. To you, the weight has just gone in a circle, but to a stationary observer the weight has traced out a helical space curve.
Log in to reply
@Brian Charlesworth – Thanks. Nice explanation.
Brian, do you do tuition classes for modern maths? ;)
I'm stuck in the old ways, I guess.
Log in to reply
Haha. No, I don't do any teaching. I don't really know what "modern maths" is; classical maths suits me just fine. :)
you can imagine that you go up the stair with uniform speed, and the vertical velocity is 10. Hence the time for you to reach the top is 1, and the speed of your circular motion is 4pi. From here you can calculate the resultant speed is sprt( 10^2 + (4pi)^2), and the distance is speed multiplied by time, which gives you 16.1 as the answer.
It forms a one complete helix.
Length of helix is = √((h^2 )+(〖2 pi r)〗^2) Circumference = 2 pi r Height of helix to complete one revolution = h
Find the length of arc for helix that will be the answer. Which is 16.1feet
In the above image, by using some good will and a lot of imagination, the line snaking the cylinder is supposed to wrap around it like the red line in the problem picture.
We begin by forming a cylinder with its top and bottom touching the end points of the red line. Then, we "unravel" the cylinder into a rectangle with two circles, one on top and one on the bottom. The height of this rectangle will be 10 (length of the blue line) and the width will be equivalent to the circumference of the top and bottom circles 2 π ( 2 ) .
Next, applying the Pythagorean theorem, we find the length of the line connecting two corners of the rectangle to be ( 4 π ) 2 + 1 0 2 ≈ 1 6 . 1
I really love this method because there is a generalized form of it (for cylinders given the height and the degree of rotation of the spiral) which I have posted here