Splitting The Sun In Two
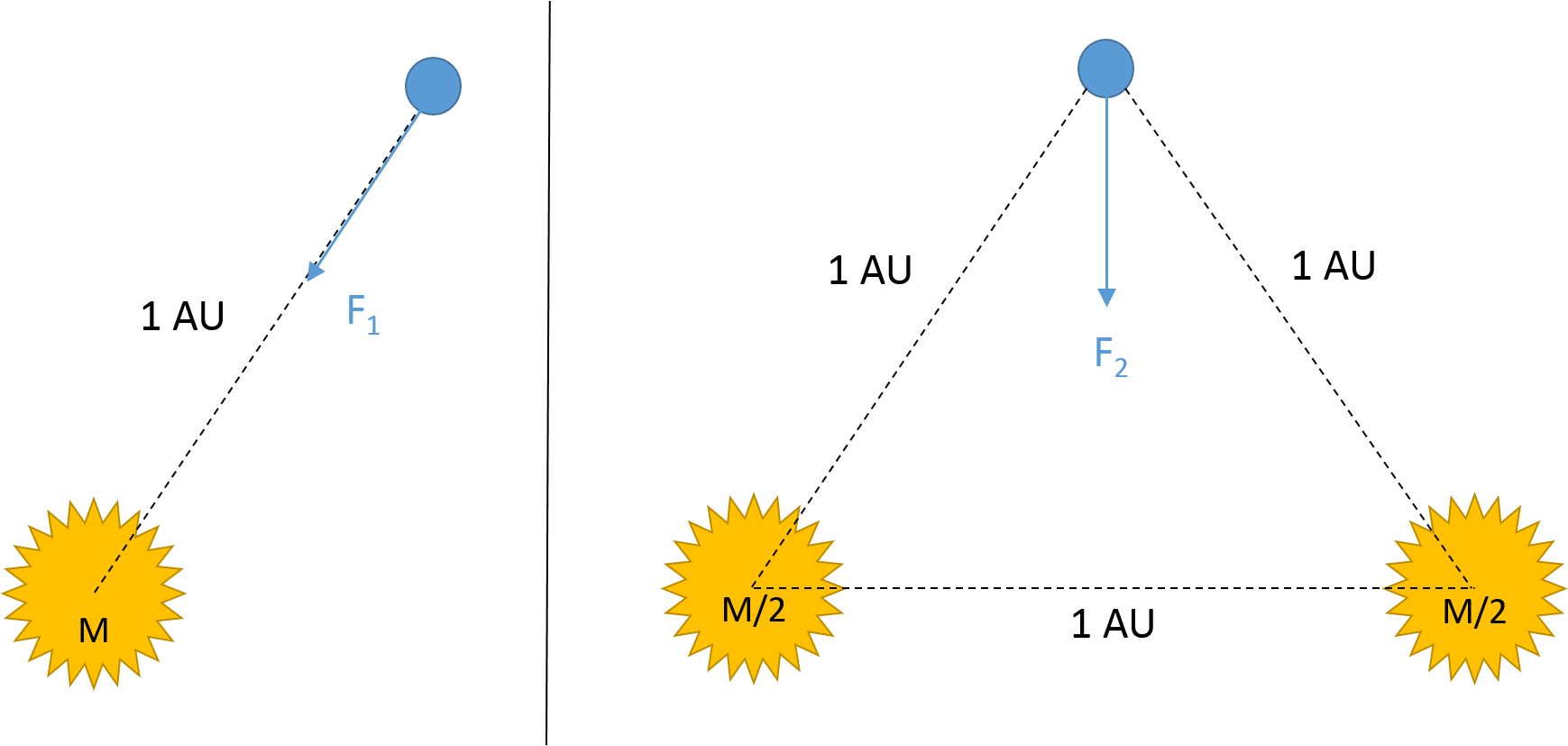
Let's imagine the Earth orbiting two stars that are separated by a distance of 1 AU , each with half the mass of the Sun. When the distance between the Earth and both stars is 1 AU , the net gravitational force acting on Earth is F 2 .
If the gravitational force applied by the Sun on the Earth at an orbital distance of 1 AU is F 1 . What is F 1 F 2 ?
Note : 1 AU , which stands for "Astronomical Unit," is the actual average orbital distance between Sun and Earth.
The answer is 0.87.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
There is some unprecision in your question with the definition of F2. Your answer is considering a total net force F2 which is oriented in the direction between the 2 suns. But if you consider the real pull by each sun, the ratio F2/F1 is 0.75.
Log in to reply
Hi Jean,
Thanks for your comment. I agree that the way that I have defined F 2 as the net force in the problem is a bit subtle and requires clarification for solvers who do not recall that net force is the vector sum of the individual pulls from each sun. Toward that end, I have modified the figure to depict the vectors with magnitudes F 1 and F 2 . Let me know if you think the new picture helps.
On a related note, please explain how you obtained the ratio F 2 / F 1 = 0 . 7 5 for the net force. The magnitude of the pull of just one of the stars should be 0 . 5 F 1 because the one star has half the Sun's total mass, and the factor of 1 / 2 carries through the calculation of force directly from Newton's gravitational law. If you combine the forces applied by each star using vector arithmetic, you should end up with a net force of 0 . 8 7 F 1 . Please help me understand what assumptions you made to calculate 0 . 7 5 F 1 so that I can remove any remaining ambiguities in the problem statement. Thanks!
Log in to reply
the new diagram is better and less ambigous for force F2 sorry, my bad for the value 0.75F1. in fact the pull from each half sun is half F1. my error is to project perpendicularly F2 (once computed from Fa and Fb ) back on the lines of Fa and Fb pull to get 0.75F1 ;-) But is this a mistake anyway? if there is only one half sun (on the left), you have only a single pull Fa = 1/2F1. But what happens when you have a second half sun (on the right) ? The second half sun will exert a second force Fb which results, by orthogonal projection on the line Eart-1rst sun (on the left), a force Fb' = 1/4F1. The sum of the force on this direction will be 1/2F1+ 1/4F1 =0.75F1. Am I correct ?
Log in to reply
@Jean David – I see what you mean, Jean. You can add these vectors in any coordinate system you choose in order to compute the vector sum. It looks like you are picking one of your coordinate directions along f a . Indeed, projecting pull f b in the direction of f a gives 0 . 2 5 F 1 , which when added to ∣ f a ∣ yields 0 . 7 5 F 1 . However, in the coordinate system you've picked, f b also has a non-zero projection onto the direction perpendicular to f a , which is equal to 4 3 F 1 . This is also a component of the net force in your coordinate system, since f a can't have a component perpendicular to itself. Adding the perpendicular components of the net force in your coordinate system and taking the magnitude should give the same result as the coordinate system I chose in the solution. Specifically, ( 4 3 F 1 ) 2 + ( 4 3 F 1 ) 2 = 2 3 F 1 . In fact, it should not matter what coordinate system you set up to add the pulls, you should end up with the same result. It's always informative (and fun) to verify coordinate independence of physical quantities in different scenarios. Thanks for your comments!
We would like to calculate the net gravitational force on the Earth in two scenarios:
When the Earth is a distance of 1 AU from the Sun; this net force is defined as F 1 in the problem.
When the Earth is a distance of 1 AU from two stars, each with half the total mass of the Sun; this net force is defined as F 2 in the problem.
The problem asks us to calculate the ratio F 1 F 2 . We will have to use Newton's Theory of Gravitation to calculate these forces.
Newton's theory states that the magnitude of the gravitational force applied by one mass M on another mass m separated by a distance R is F = R 2 G m M where G is the the gravitational constant. The direction of this force, which is crucial to solving this problem, is along the line connecting the centers of the two masses. Gravity is an attractive force, so the force on mass m is directed toward the other mass M .
Let's start by expressing F 1 in terms of the mass of the Earth m ⊕ , the mass of the sun M ⊙ and the separation distance R = 1 AU . In an Earth-Sun system, there is only one gravitational force acting on the Earth, so the magnitude of the net force is F 1 = R 2 G m ⊕ M ⊙ .
Now we will calculate F 2 , the magnitude of the net gravitational force on Earth when the Sun is split into two stars to form a binary system. The net force F 2 requires a bit more analysis because each star applies a gravitational force on m ⊕ , and these two forces are not in the same direction, so the net force is the vector sum of two forces.
Let's call the magnitude of the force applied by one of the stars on Earth f . We observe that each star applies a force of the same magnitude because the two stars have identical masses ( M ⊙ / 2 ) and they are equidistant from Earth. Applying Newton’s gravitational law again, we find f = 2 R 2 G m ⊕ M ⊙ = 2 1 F 1 . We conclude that the magnitude of the gravitational force applied by one of the stars is exactly half of F 1 . However, the two forces applied are not in the same direction; they are directed toward the centers of each star as show in this figure:
To finish the calculation of F 2 , we will add these two forces acting on the Earth using vector addition. This requires setting up a coordinate system and breaking each of the two forces into components. The diagram above depicts a suggestion for one choice of coordinate system, with the x -axis parallel to the line connecting the centers of the two stars. Since the Earth and two stars are on the vertices of an equilateral triangle, the force pictured on the left ( f a ) makes an angle 4 π / 3 with the positive x -axis. Therefore, its components are f a , x = 2 1 F 1 cos ( 4 π / 3 ) = − 4 1 F 1 and f a , y = 2 1 F 1 sin ( 4 π / 3 ) = − 4 3 F 1 . Likewise, the force pictured on the right ( f b ) in the diagram makes an angle 5 π / 3 with the positive x -axis, and therefore, it has components f b , x = 2 1 F 1 cos ( 5 π / 3 ) = 4 1 F 1 and f b , y = 2 1 F 1 sin ( 5 π / 3 ) = − 4 3 F 1 .
Adding the x -components of the two forces yields F 2 , x = f a , x + f b , x = 0 N since they are equal but opposite. However, the y -components do not cancel: F 2 , y = f a , y + f b , y = − 2 4 3 F 1 . Therefore the magnitude F 2 = F 2 , x 2 + F 2 , y 2 = 2 3 F 1 . Dividing by F 1 yields the ratio we set out to calculate: F 1 F 2 = 2 3 ≈ 0 . 8 7 .
Therefore, we calculated that the net gravitational force felt by Earth when it is equidistant from two stars whose total mass equals the Sun’s mass is about 8 7 % of the force felt by Earth when it is the same distance from the Sun.