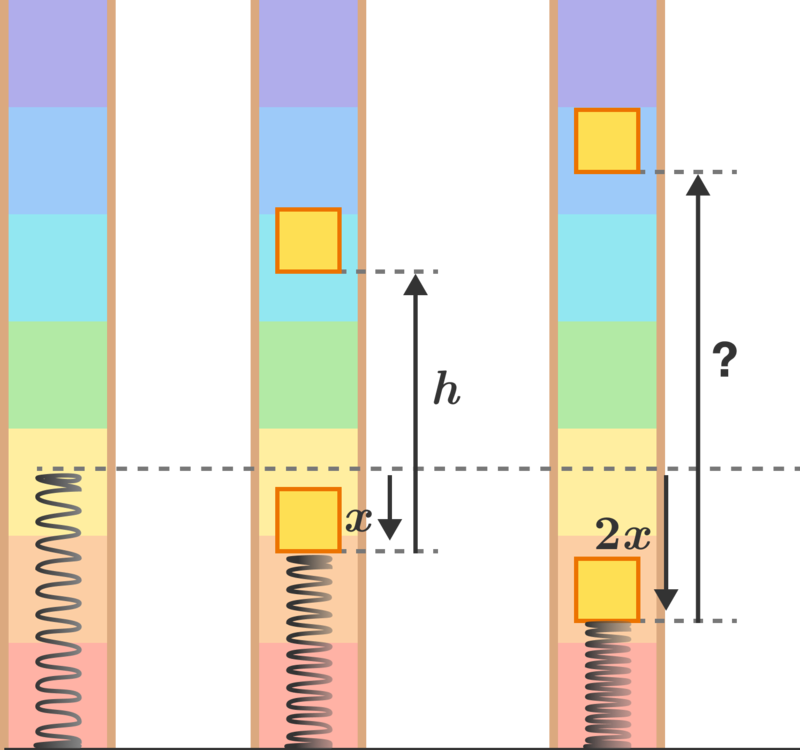
Spring loaded block

The potential energy of the spring is proportional to the square of the distance from the starting point. If it's twice the distance from the starting distance $x$ , then there's $2^2 = 4$ times potential energy. This equals $mg*(height)$ , so height is proportional to the potential energy of the spring .

We just said there's four times as much potential energy, so thing goes four times as high.

In both the cases I applied law of conservation of energy. In both the cases kinetic energy will be zero at the starting point and ending point as finial and initial velocities are zero. The equilibrium position of the spring is my datum line. The height we have to find our is assumed as $h'$ .

First Case : $\begin{array}{c}~ \dfrac12 kx^2 - mgx = mg(h - x) \\ \dfrac12 kx^2 - mgx = mgh - mgx \\ \boxed{\color{#3D99F6}mgh = \dfrac12 kx^2} \quad --- (1) \\ \end{array}$ Second Case : $\begin{array}{c}~ \dfrac12 k(4x^2) - mg(2x) = mg(h' - 2x) \\ 4 \times \dfrac12 kx^2 - 2mgx = mgh' - 2mgx \\ {\color{#3D99F6}mgh' = 4 mgh} \quad (\text{From equation 1}) \\ \boxed{\color{#20A900}h' = 4h} \\ \end{array}$

All the solutions I've seen assume that h is greater than x: it looks like it in the picture, but that's no excuse! There are two possibilities with h less than x: (1) the block remains in contact with the spring in both cases. This gives height reached as 2x+h, but we're assuming that this height is less than or equal to 2x, so this solution is possible only if h is less than or equal to zero; (2) the block loses contact with the spring in the second (2x) case. This gives height reached as 4x^2/(2x-h), and in the boundary case where h = x this boils down to 4h.

The force exerted by a spring compressed by $x$ is given by $F=kx$ , where $k$ is the spring constant. The work done by the spring on the block is $W=Fx \propto kx^2 = k_1x^2$ , where $k_1$ is a constant. When the block on the spring is released, all the work done by the spring is converted to the potential energy of the block when it reaches its highest point $h$ from the point of release. That is $k_1x^2 = mgh$ , where $m$ is the mass of the block and $g$ is the acceleration due to gravity. When the spring is compressed by $2x$ , then $k_1(2x)^2 = 4k_1x^2 = 4mgh$ , the block reaches a height of $\boxed{4h}$ .

Use elimination (and common sense):

The answer can't be $h/2$ because it doesn't make sense for the block to go lower when you apply more force.

The answer can't be $h$ because applying more force would make the block go higher and not stay at the same height.

The answer is most likely not simply $2h$ because questions like this one are usually trick questions (in a sense) so the answer wouldn't be just simple multiplication. (You would know this if you have experience with multiple choice questions)

So the answer has to be $4h$ , because it makes the most sense and it is the most likely answer.

Note: I know that in the question, it actually says "1/2h" and not "h/2" (like I put down) but when I write "1/2h" in the solution, it looks like the h is in the denominator and not the numerator so I just used "h/2".

The potential energy of the block of wood when the string is compressed by $X$ from it's natural length:

$\begin{aligned} E &= \int_{-X}^{0}-kx \,dx \\ &= \int_{0}^{X}kx\,dx = \frac{kX^{2}}{2}\end{aligned}$

or, $E \propto x^{2}.$

The gravitational potential energy of the block of wood at the moment when it reaches maximum height H:

$E = mgH$

or, $E \propto H.$

Hence, by conservation of energy, $H \propto x^{2}$ and thus the answer is $\boxed{4h}.$

How high the mass goes depends completely on the amount of potential energy that the spring has in store (which is being fully transferred to the mass on release). Now the potential energy of a compressed spring is given as 1/2 kx^2 . This is being completely transferred to the mass, which again uses it all up as its kinetic energy until it reaches a maximum height h where his potential energy mgh is equal to the energy given by the spring. so, mgh = 1/2 kx^2 . or, h is proportional to x^2 .

Thus when the compression is doubled, the maximum height reached will increase by four times i.e. the mass will reach 4h.

Energy stored is proportional to x^2 and therefore height is 4h.

Work-Energy Theorem: Just use the potential energy of spring and potential energy of block with respect to the ground for two test cases, (1) for initial case, when spring is stretched with the block and (2) when the block is released in the air.

Short answer: spring energy goes as the square of the distance, potential energy is linear to the height (uniform field). In formula form $\frac{1}{2}kx^2$ versus $mgh$ , where k,m, and g are constants and x plays the same rôle as h. Therefore the answer is 4 times.

More elaborate answer: in this problem engergy is constantly exchanged between 3 forms: gravitational potential energy $V=mgh$ , spring energy $S=\frac{1}{2}kx^2$ and kinetic energy $T=\frac{1}{2}mv^2$ . We will assume there is no energy dissipation, because the problem gives us no information about it. And since we only look at moments where v=0, we can forget about T.

Set h=x, which is 0 at equilibrium for the unloaded spring. When a weight is put on the spring, it reaches an equilibrium at the point x where /(S=-V/). For amplitudes smaller than this, the block will just go up and down, keeping contact with the spring. Only when we press it down with at least its own weight, the block will raise enough to get loose from the spring. But this does not worry us, the spring energy is 0 whenever the block is loose from it.

Case 1: V+S = $-mgx+\frac{1}{2}kx^2$ when at top $y_1$ , all energy is gravitational so that

$mgy_1=-mgx+\frac{1}{2} kx^2$ => $y_1=(-mgx+1/2 kx^2)/mg=-x+\frac{(1/2kx^2)}{mg}$

Case 2: V+S = $-2mgx+\frac{1}{2}k(2x)^2$ when at top $y_2$ , all energy is gravitational so that

$mgy_2=-2mgx+\frac{1}{2} k(2x)^2$ => $y_2=(-2mgx+2kx^2)/mg=-2x+\frac{2kx^2}{mg}$

Now $h = y_1+x= \frac{\frac{1}{2} kx^2}{mg}$ and $?=y_2+2x=\frac{2 kx^2}{mg} = 4h$ .