Springs and SHM - 2
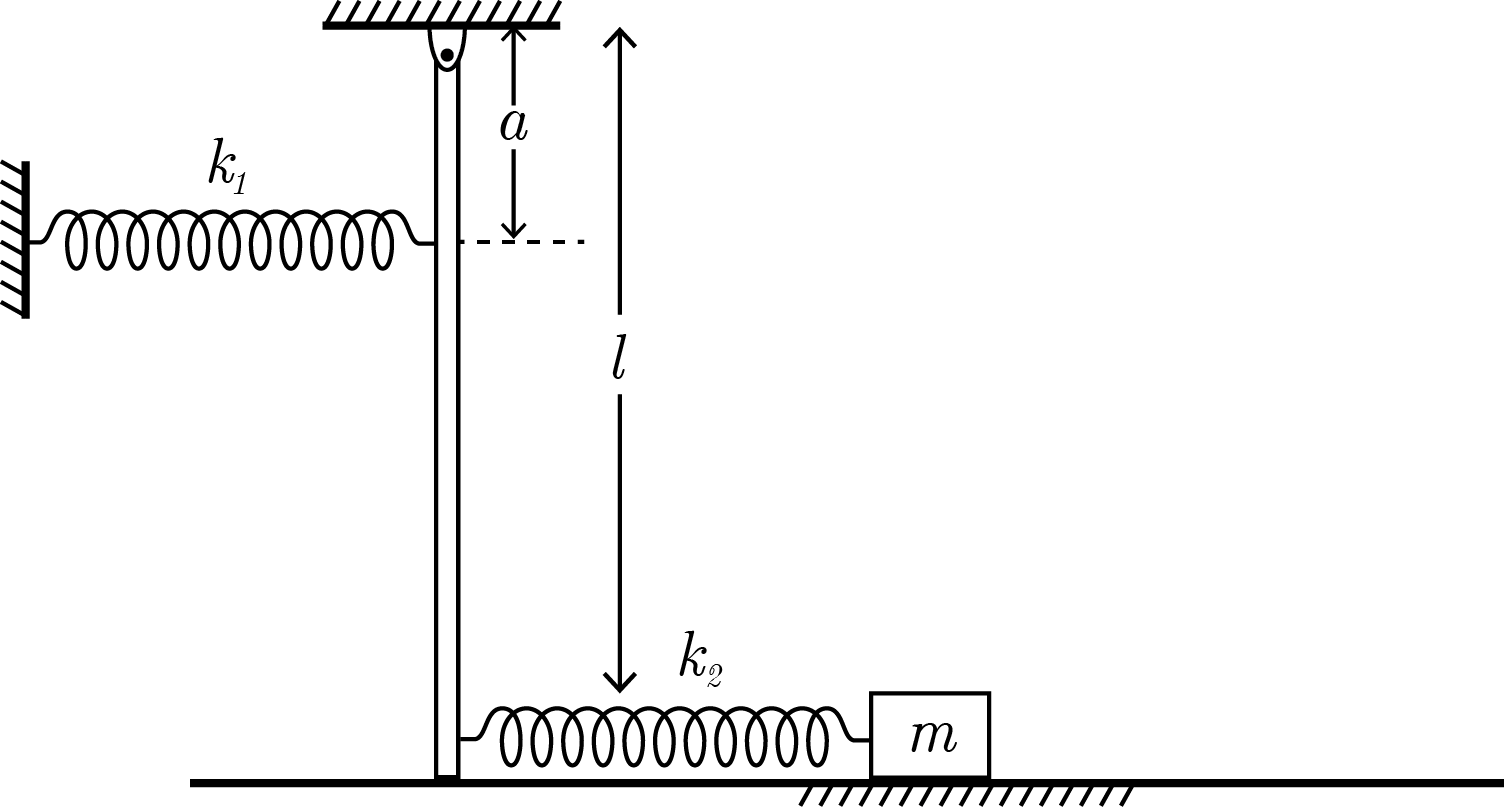
A very light rod of length ℓ pivoted at O is connected with two springs of stiffness k 1 and k 2 at a distance a and ℓ from the pivot respectively. A block of mass m attached with the spring k 2 is kept on a smooth horizontal surface. If the angular frequency of small oscillation of the block m is ω , find ⌈ 1 0 0 0 ω ⌉
Details
- m = 1 0 k g , k 1 = 2 3 N m − 1 , k 2 = 3 4 N m − 1 , l = 1 m , a = 4 3 c m
This Question is not Original
The answer is 615.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
This is a very clear approach that cuts through some needless steps. Great insight with the zero-torque requirement on the massless rod, perhaps some further explanation of this step would benefit others. Excellent solution.
@Brilliant Physics , can you please explain where and how should I elaborate more?
Log in to reply
I think you should add an explanation of why a massless rod has zero torque.
Did the same thing, forgot to take the square root and hence entered 578! Feel so bad, especially when there is no credit for working.
Log in to reply
even i did the same mistake ...and btw it comes out to be 378
can u explain how u wrote extensions
Log in to reply
Where did you not understand, in which case?
Log in to reply
sorry for late reply . i didnt understand extension a for spring 1 and x-l for 2nd
Log in to reply
@Dhruv Aggarwal – It's fine! Suppose the rod turns a very small degree δ θ w.r.t vertical. So the extension of Spring 1 becomes a δ θ because d l = r d θ . If we displace (elongating the Spring 2) the block slightly by δ x , since the rod shortens it to ℓ δ θ , the net extension becomes ( δ x − ℓ δ θ )
Log in to reply
@Kishore S. Shenoy – okay thanks . i was thinking wrongly that extensions should be same .. my bad
what is x ? bro @Kishore S Shenoy and how is x related by theta like that it would be good if you explain !
Nice problem!
I made a mistake by writing extension in second spring as x+l(theeta).
SOLUTION IS EPIC
Log in to reply
Glad you liked it!
btw do u recommend level 5 brilliant questions for iit jee ?
but the forces due to both the springs are producing torques in same direction ( anticlockwise if the lower one is compressed) how come they cancel each other? are you not taking torques from hinge point? or is it that when lower spring is compressed the block displaces more and thus causing an extension?
Log in to reply
Yes. Thus the net torque on the rod CAN be zero. If it's not, the net angular acceleration would be infinite.
As the rod is light the spring with stiffness k1 can be shifted from distance a to the distance l from the pivot with a equivalent spring of stiffness k1(a/l)^2. Then we see that the springs are in series and we find the net stiffness. This comes out to be 3.7799. Then finding angular frequency is easy.
nice method
What if rod has mass
i did by your method bro ! you rock !
Let us consider a hypothetical spring of stiffness k at the bottom which is opposite to the spring k 2 instead of the spring with stiffness k 1 .
So the elastic potential energy stored in both the springs are equal.
The extension in the springs are a θ & l θ for k 1 & k respectively.
So by equating their energies we get,
k = l 2 k 1 a 2
We also know that these two springs are connected in series.So the equivalent stiffness is ,
k e f f 1 = k 2 1 + k 1
k e f f = k 1 a 2 + k 2 l 2 k 1 k 2 a 2
On equating the force,
k e f f x = m ω 2 x
On substituting the values we get
ω = 0 . 6 1 4 8
Since the rod is light, net torque on it will be zero. To find net extension in the second spring, we use this equation. First, let θ be the angle made by the rod at the extreme position. Thus the net extension in the second spring will be x − ℓ θ . So, balancing torques k 1 a 2 θ = k 2 ℓ ( x − ℓ θ ) ⇒ ℓ θ = a 2 k 1 + ℓ 2 k 2 k 2 ℓ 2 x
Thus, the force on the block is only due to the second spring, F = − k 2 ( x − ℓ θ ) = − a 2 k 1 + ℓ 2 k 2 k 1 k 2 a 2 x
Thus, by definition : ω = m ( a 2 k 1 + ℓ 2 k 2 ) k 1 k 2 a 2