Springs, inclines, friction, projectile, what not?

Classical Mechanics Level 5

A block of mass 5 kg 5 \text{ kg} rests on top of the tail of a plane of inclination 3 0 ∘ 30^\circ preceded by a spring of constant 2 N/m 2 \text{ N/m} and contraction 1 m 1 \text{ m} . The coefficient of friction between the tail surface and the block is 0.2 0.2 . As soon as the spring is released, the plane begins to move in forward direction with an acceleration of 1 m/s 2 1 \text{ m/s}^2 . It takes the block 3 3 seconds to reach the bottom of the tail. As soon as the block reaches the bottom of the tail, the plane stops immediately in mid air. The distance between the tail and the tip of the plane is 2 m 2 \text{ m} . The coefficient of friction between the block and the horizontal surface of the plane is 0.3 0.3 . The block continues to move over the horizontal surface and falls off the tip of the plane. If the plane was flying at a height of 50 m 50 \text{ m} above the ground, then find the distance of the final position of the block from the tip of the plane.

The figure below would help in understanding the situation.

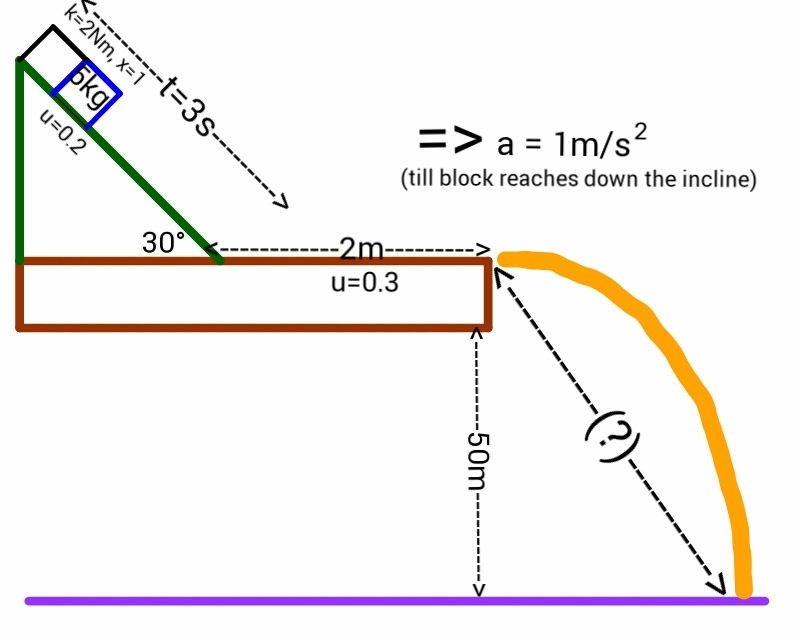
Details and assumptions :-

  • Neglect the air resistance.
  • Assume that the block does not rebound after hitting the ground for the first time.
  • Assume that the plane is of negligible width.
  • Assume that the tip of the plane is flat (as shown in figure) and not conical.
  • The plane travels in the direction indicated by the ⟹ \implies shown in the figure.
  • Take g g (acceleration due to gravity) as 10 m/s 2 10 \text{ m/s}^2 .
  • Give your answer (in metres) to the nearest integer.


The answer is 56.

Ashish Menon by Ashish Menon , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Ashish Menon
Aug 7, 2016

Taking components, frictional force = μ ( m g cos ⁡ 30 ° + m a sin ⁡ 30 ° ) = 0.2 ( 50 × 3 2 + 5 × 1 × 1 2 ) = 9.160 \mu\left(mg \cos{30}^° + ma \sin{30}^°\right)\\ \\ = 0.2\left(50× \dfrac{\sqrt{3}}{2} + 5×1×\dfrac{1}{2}\right)\\ \\ = 9.160

The net force is force in down the incline - force up the incline.
m g sin ⁡ 30 ° + k x − 9.160 − m a cos ⁡ 30 ° = m × A 25 + 2 − 9.160 − 5 × 3 2 = 5 × A A = 2.702 \begin{aligned} mg\sin{30}^° + kx - 9.160 - ma\cos{30}^° & = m × A\\ \\ 25 + 2 - 9.160 - 5×\dfrac{\sqrt{3}}{2} & = 5 × A\\ \\ A & = 2.702 \end{aligned}

Kinetic energy gained by block at time of release of spring = 1 2 k x 2 = 1 2 × 2 × 1 2 = 1 J \dfrac{1}{2} kx^2\\ = \dfrac{1}{2}×2×1^2\\ = 1J

1 = 1 2 × m v 2 v = 2 5 v = 0.632 m / s \begin{aligned} 1 & = \dfrac{1}{2}×mv^2\\ \\ v & = \sqrt{\dfrac{2}{5}}\\ \\ v & = 0.632 m/s \end{aligned}

Velocity at bottom of tail = u + a t = 0.632 + 2.702 × 3 = 8.738 u + at\\ = 0.632 + 2.702×3\\ = 8.738

Kinetic energy at bottom = 1 2 × m v 2 = 1 2 × 5 × ( 8.738 ) 2 = 190.890 J \dfrac{1}{2} × mv^2\\ \\ = \dfrac{1}{2} × 5 × {(8.738)}^2\\ \\ = 190.890 J

Work done by frictional force on horizontal surface = F × S = μ × m × g × S = 0.3 × 5 × 10 × 2 = 30 J F × S\\ = \mu × m × g × S\\ = 0.3 × 5 × 10 × 2\\ = 30 J

So, energy left at the tip of the plane = 190.890 − 30 = 160.890 J 190.890 - 30\\ = 160.890 J

1 2 × m v 2 = 160.890 v = 160.890 × 2 5 v = 8.022 m / s \begin{aligned} \dfrac{1}{2} × mv^2 & = 160.890\\ \\ v & = \sqrt{\dfrac{160.890 × 2}{5}}\\ \\ v & = 8.022 m/s \end{aligned}

Now, horizontal distance travelled by projectile of block = v × 2 h g = 8.022 × 2 × 50 10 = 25.368 m v × \sqrt{\dfrac{2h}{g}}\\ \\ = 8.022 × \sqrt{\dfrac{2×50}{10}}\\ \\ = 25.368 m .

So, distance from tail can be found by using Pythagoras' theorem:-
S ′ = ( 50 ) 2 + ( 25.368 ) 2 = 56.067 ≈ 56 m \begin{aligned} S' & = \sqrt{{(50)}^2 + {(25.368)}^2}\\ \\ & = 56.067\\ \\ & \approx \color{#3D99F6}{\boxed{56 \ \text{m}}} \end{aligned}

3 Helpful 0 Interesting 0 Brilliant 2 Confused

Very nice question, just a small correction in the statement of the question... units of spring constant are N/m \text{N/m}

Swagat Panda - 4 years, 10 months ago

Log in to reply

Thanks for your most valued comments :) I corrected the typo you mentioned.

Ashish Menon - 4 years, 10 months ago

In first case,while calculating net force when it is going down the incline,how did u write macos30=2.5×root3/2??shouldn't it be 5×root3/2??

Tanishq Nandan - 4 years, 10 months ago

Log in to reply

Thanks for mentioning, it was just a typo I corrected it. The answer is nevertheless same. :)

Ashish Menon - 4 years, 10 months ago

You are taking the force of the spring as constant when calculating acceleration, and then you calculate the speed with the kinetic energy because is not constant.

Juan Escamilla Anguiano - 4 years, 10 months ago

Log in to reply

Force of spring is in fact constant at time of release because initially t=0, and force is imparted over a tiny interval so, that assumption is correct. Kinetic energy at bottom is calculated so the not constant thingy does not make a difference.

Ashish Menon - 4 years, 10 months ago

Log in to reply

But you use the acceleration calculated with the force of the spring as constant, and multiply by the time of 3 s. I think you need to remove the force of the spring of the total force, because you are taking the effect of the spring in the potential energy anyway.

Juan Escamilla Anguiano - 4 years, 10 months ago

Log in to reply

@Juan Escamilla Anguiano – No, I didnt take the effect of the spring as potential energy. If I had, then I would have had to subtract 1/2 kx^2 from my final answer. Also note that the force given is kx. We cant deny the fact of spring's extension. If we did, then it would be just the same as block slips down an incline, but spring provides it with some initial velocity which would have been 0 if we neglected it.

Ashish Menon - 4 years, 10 months ago

Log in to reply

@Ashish Menon – There is no initial velocity, the potential energy of the spring become kinetic energy of the block, over the full extension of the spring, that speed is provided when the spring extension is 0. So the force that generate the acceleration must not have the force of the spring because you add the speed provided by the spring.

Juan Escamilla Anguiano - 4 years, 10 months ago

When the block is still in contact with the spring, will gravity, friction, and the pseudo force not act on it?
Please check if my approach is correct :-
I will first apply law of conservation of energy to calculate the velocity of block just as it loses contact with spring. The work done by gravity, pseudo force, friction and the spring is equal to the change in kinetic energy of the block(you only took work done by spring).
m g sin ⁡ 30 + 1 / 2 k x 2 − 5 sin ⁡ 60 = 1 / 2 m v 2 + μ ( m g cos ⁡ 30 + 5 cos ⁡ 60 ) mg \sin 30 +1/2kx^2-5 \sin 60=1/2mv^2+ \mu (mg \cos 30 +5 \cos 60)
Solving this yields v 2 ≈ 5 ⟹ v = 5 v^2 \approx 5 \implies v = \sqrt {5} as compared to your v = 0.632. v=0.632.

Rest all other steps after that are same and I got the answer as ≈ 56.7 \approx 56.7

Nonetheless, Beautiful Question !! \color{#D61F06}{\large{\text{Beautiful Question !!}}}

Harsh Poonia - 2 years, 3 months ago

You also made a big blunder when calculating the acceleration, because the force k x kx by the spring will not act throughout the journey on the incline. It stops acting when the block leaves contact with the spring. So the correct method should be to first calculate the final velocity till the time the block is in contact with the spring, and then consider only the pseudo force, gravity and friction to calculate your ′ A ′ 'A ' . The correct answer to this problem would then be 57 \large{\boxed{57}} (rounding off 56.7 to nearest integer.

Harsh Poonia - 2 years, 3 months ago

1 pending report

Vote up reports you agree with

×

Problem Loading...

Note Loading...

Set Loading...